- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Подборка увлекательных и познавательных задач с применением логики и пространственного мышления
Содержание
- 1. Подборка увлекательных и познавательных задач с применением логики и пространственного мышления
- 2. Учимся геометрии Задача о пауке и мухе.12345Тестовые
- 3. 1.Задача о пауке и мухе.Представим себе, что
- 4. MP Любую гипотезу -необходимо доказывать.Как добраться пауку
- 5. 3.Задача о пауке и мухе.Муха хочет пересечь
- 6. В двух противоположных углах коробки
- 7. 5.Задача о пауке и мухе.Комната имеет форму
- 8. Поделите отрезок пополам.Известно, что в трапеции прямая,
- 9. Восстановите треугольник.Даны три прямые, которые пересекаются в
- 10. Длина экватора и апельсин.Представим, что Земной шар
- 11. Вниз по наклонной.Если шар, гладкий куб и
- 12. Увеличение пруда.Решение:Пруд имеет форму квадрата, по углам
- 13. Геометрический принцип.
- 14. Ребро куба. Четыре треугольника.Имеется куб, который
- 15. На рисунке показан кирпич. Придумайте способ
- 16. Требуется построить ломаную из четырех
- 17. В одной сказке хозяин, нанимая
- 18. РешениеЗадачи на построение.Как построить угол
- 19. 1. Разные способы.Высоты треугольника АВС,
- 20. 2. Разные способы.Докажите, что треугольник, в
- 21. Если две стороны одного треугольника
- 22. 3. Периметр равностороннего треугольника АВС равен
- 23. 3.Тестовые вопросы.1) Существует треугольник, сторона
- 24. 4.Тестовые вопросы.1) Центром симметрии квадрата
- 25. 5.Тестовые вопросы.1) Если радиус круга
- 26. 6.Тестовые вопросы.1) Если один из
- 27. 7.Тестовые вопросы.1) ромб, диагонали которого
- 28. 8.Тестовые вопросы.1) В прямоугольном треугольнике суммакатетов
- 29. Около любого квадрата можно описать
- 30. 10.Тестовые вопросы.1) Смежные углы равны.2)
- 31. 1.Поразмышляем.4. Чему равен угол между биссектрисами
- 32. 2. Выберите из 5 терминов:
- 33. 3.Поразмышляем.1. Можно ли треугольник разбить
- 34. 4.Поразмышляем.2. Может ли угол при
- 35. 5.Поразмышляем.3. Найдите
- 36. 6.Поразмышляем.3. Найдите величинуугла AВC. 4. Дан
- 37. 7.Поразмышляем.2. Длины двух смежных сторон параллелограмма
- 38. 8.Поразмышляем.Решение1. Развёртка какого прямоугольногопараллелепипедадана на рисунке?2.
- 39. 9.Поразмышляем.Решение1. Каждую из данных фигур можно превратить
- 40. 10.Поразмышляем.1. Каждую из фигур надо разрезатьна
- 41. Тест1. Выбор ответов.В 11. Укажите номера верных
- 42. Тест2. Выбор ответов.В 11. Укажите номера верных
Слайд 1
Учимся геометрии
Подборка увлекательных задач
с применением логики и
пространственного мышления
Сборник задач
учитель математики
МБОУ Лицей №1 им. Г.С. Титова г. Краснознаменска
Слайд 2
Учимся геометрии
Задача о пауке и мухе.
1
2
3
4
5
Тестовые вопросы.
1
2
3
4
5
6
7
8
9
10
Поразмышляем.
1
2
3
4
5
6
7
8
9
10
Поделите отрезок пополам.
Восстановите треугольник.
Длина
Вниз по наклонной.
Увеличение пруда.
Геометрический принцип.
Ребро куба.4 треугольника.
Диагональ кирпича.
Девять точек.
Бочка наполовину.
Задачи на построение.
Разные способы.
1
2
Выбор ответов.
1
2
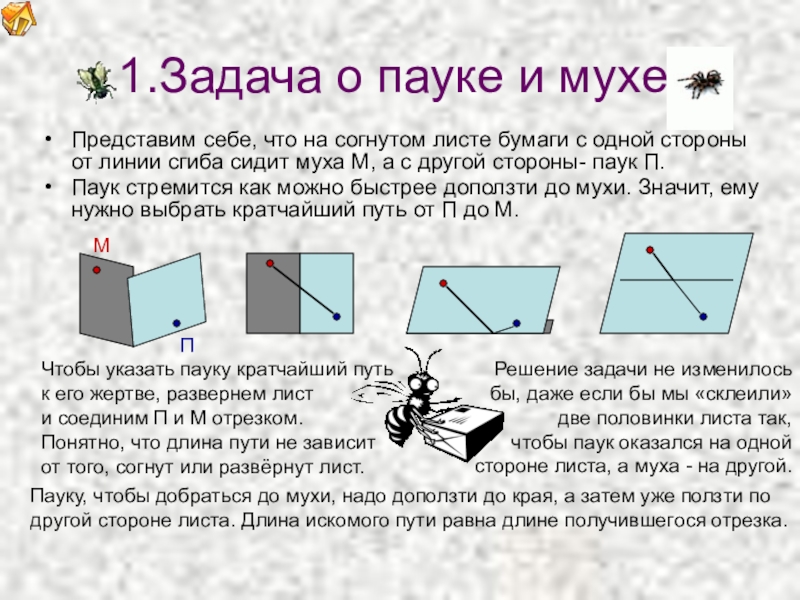
Слайд 31.Задача о пауке и мухе.
Представим себе, что на согнутом листе бумаги
Паук стремится как можно быстрее доползти до мухи. Значит, ему нужно выбрать кратчайший путь от П до М.
Чтобы указать пауку кратчайший путь
к его жертве, развернем лист
и соединим П и М отрезком.
Понятно, что длина пути не зависит
от того, согнут или развёрнут лист.
Решение задачи не изменилось
бы, даже если бы мы «склеили»
две половинки листа так,
чтобы паук оказался на одной
стороне листа, а муха - на другой.
Пауку, чтобы добраться до мухи, надо доползти до края, а затем уже ползти по
другой стороне листа. Длина искомого пути равна длине получившегося отрезка.
М
П
Слайд 4
M
P
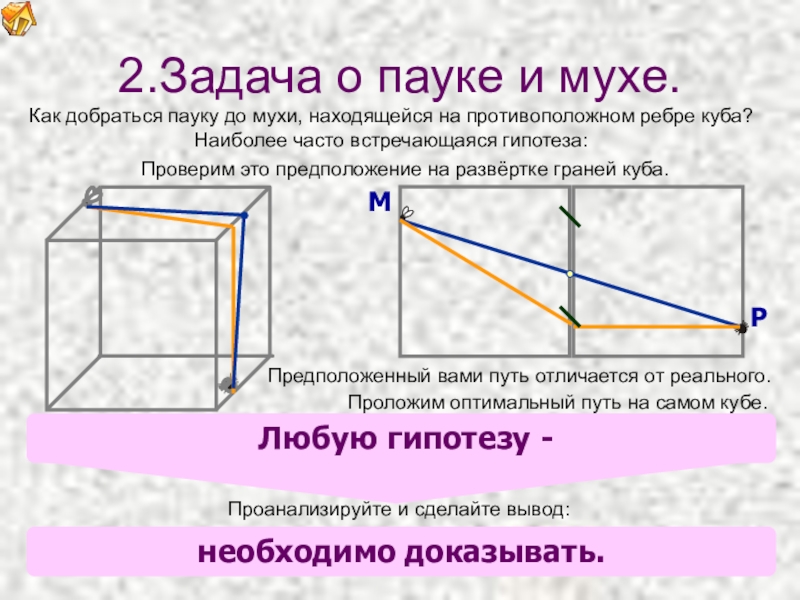
Любую гипотезу -
необходимо доказывать.
Как добраться пауку до мухи, находящейся на
Наиболее часто встречающаяся гипотеза:
Проверим это предположение на развёртке граней куба.
Предположенный вами путь отличается от реального.
Проанализируйте и сделайте вывод:
2.Задача о пауке и мухе.
Проложим оптимальный путь на самом кубе.
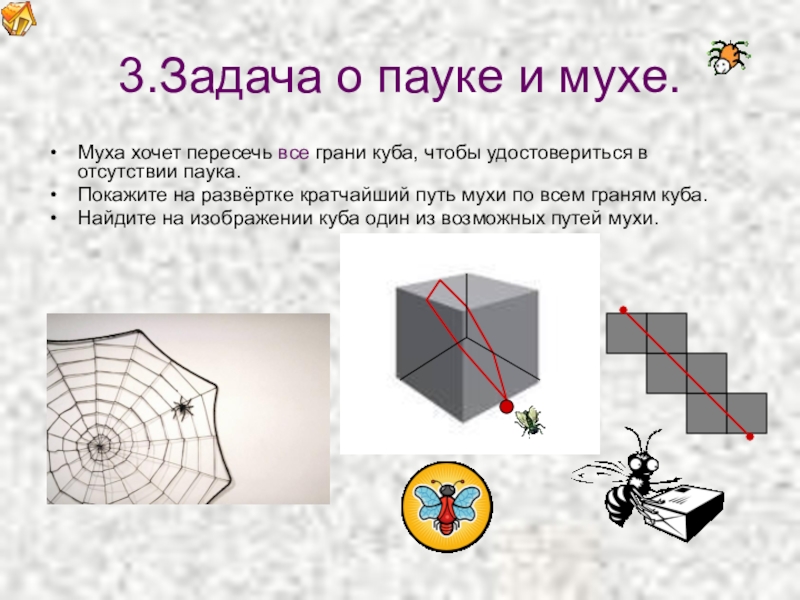
Слайд 53.Задача о пауке и мухе.
Муха хочет пересечь все грани куба, чтобы
Покажите на развёртке кратчайший путь мухи по всем граням куба.
Найдите на изображении куба один из возможных путей мухи.
Слайд 6
В двух противоположных углах коробки сидят муха и
Решение
Вычертим развертки граней и покажем на них движение паука в первом (по двум боковым граням) и втором случаях ( по боковой и верхней граням).
Длиннее первый путь, следовательно, необходимо, выбирая самый короткий, двигаться сначала по боковой, затем по верхней грани.
4.Задача о пауке и мухе.
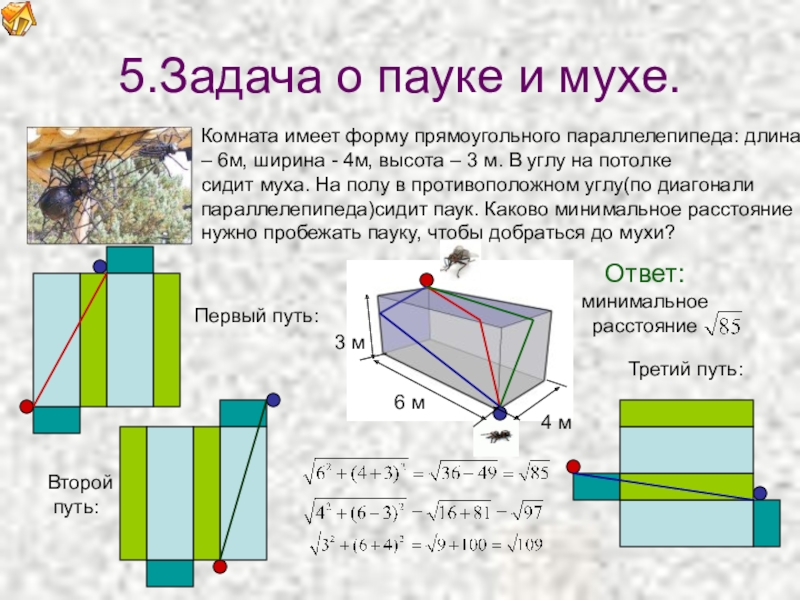
Слайд 75.Задача о пауке и мухе.
Комната имеет форму прямоугольного параллелепипеда: длина –
сидит муха. На полу в противоположном углу(по диагонали параллелепипеда)сидит паук. Каково минимальное расстояние
нужно пробежать пауку, чтобы добраться до мухи?
6 м
4 м
3 м
Первый путь:
Второй
путь:
Третий путь:
Ответ:
минимальное
расстояние
Слайд 8Поделите отрезок пополам.
Известно, что в трапеции прямая, проведённая через середины оснований
Как использовать этот факт при решении следующей задачи: «Даны отрезок АВ и параллельная ему прямая а. Разделите отрезок АВ пополам при помощи одной линейки без делений»?
1. Возьмите произвольную точку С на плоскости.
2. Проведите две прямые через концы
отрезка А и В и эту точку С.
3. В образовавшейся трапеции
проведите диагонали, получится
Д-точка пересечения
диагоналей.
4. Проведите прямую через точку С и точку Д, она разделит отрезок АВ
пополам.
А
В
С
Д
Решение:
Слайд 9Восстановите треугольник.
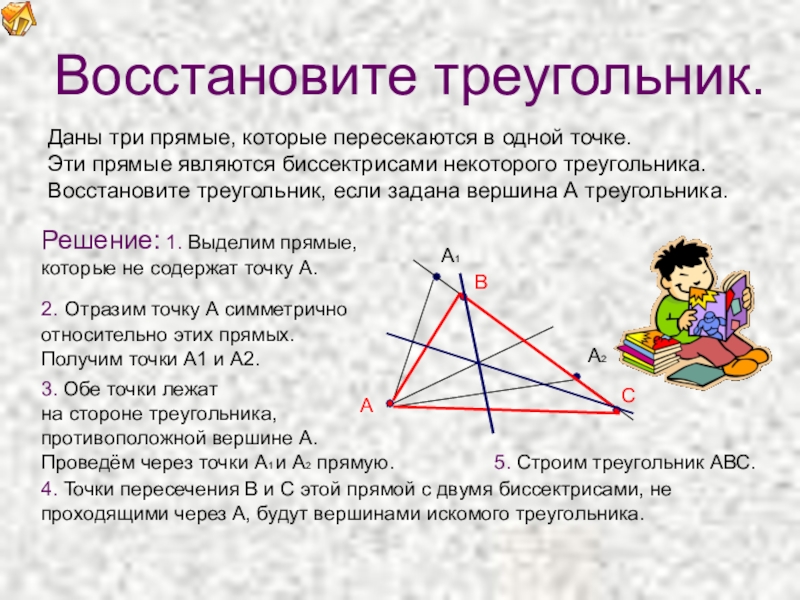
Даны три прямые, которые пересекаются в одной точке.
Эти прямые являются
Восстановите треугольник, если задана вершина А треугольника.
2. Отразим точку А симметрично
относительно этих прямых.
Получим точки А1 и А2.
3. Обе точки лежат
на стороне треугольника,
противоположной вершине А.
Проведём через точки А1 и А2 прямую.
А1
А2
4. Точки пересечения В и С этой прямой с двумя биссектрисами, не проходящими через А, будут вершинами искомого треугольника.
В
С
А
5. Строим треугольник АВС.
Решение: 1. Выделим прямые,
которые не содержат точку А.
Слайд 10Длина экватора и апельсин.
Представим, что Земной шар обтянут по экватору обручем,
Пусть длина окружности Земли = С (м), апельсина = с (м).
Радиус Земли равен ( )м, а радиус апельсина ( )м.
Далее вообразим, что окружность каждого
обруча увеличилась на 1м. Чей зазор
больше – апельсина или Земного шара?
Ответ: зазоры равны.
После прибавки к обручу 1 м окружность
Земли стала равна ____ м, окружность апельсина _____ м.
Радиусы же их будут R= , r= .
Зазор есть разность между новым и старым радиусами.
Решение:
С+1
с+1
Если вычесть, то получим одинаковые приращения:
Слайд 11Вниз по наклонной.
Если шар, гладкий куб и цилиндр будут одновременно пущены
Шар и цилиндр потратят часть энергии на вращение, что соответственно уменьшит их скорость.
Решение:
Первым достигнет низа _____, вторым – _____, последним - _____
КУБ
ШАР
ЦИЛИНДР
Слайд 12Увеличение пруда.
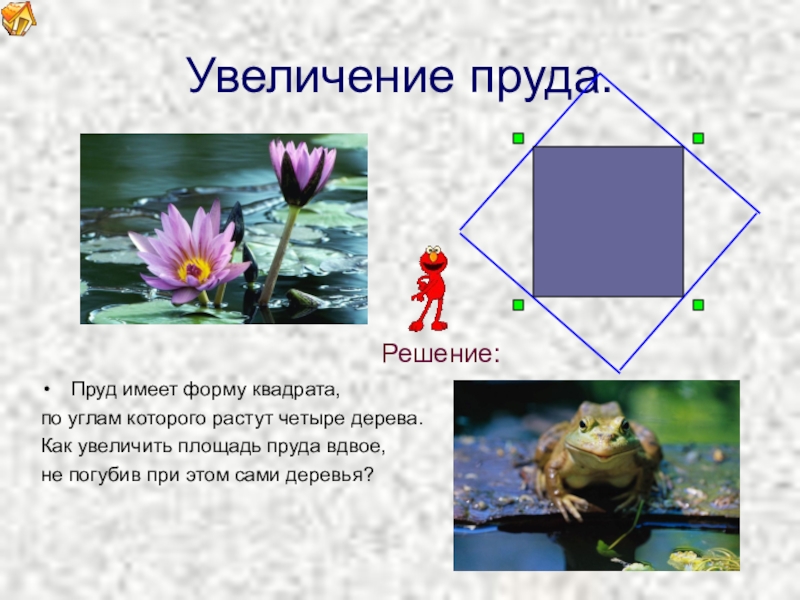
Решение:
Пруд имеет форму квадрата,
по углам которого растут четыре дерева.
Как увеличить площадь пруда вдвое,
не погубив при этом сами деревья?
Слайд 13Геометрический принцип.
Задача 1.
Длины
треугольника
выражаются целым числом
дециметров.
Одна сторона 3 дм,
другая 1 дм.
Каков периметр
треугольника?
Какой геометрический принцип лежит в разбивке букв по следующим группам:
I -А, Д, М, П, Т, Ф, Ш;
II -В, Е, З, К, С, Э, Ю;
III - О, Ж, Х, Н,
IV -Б, Г, Л, И, Р, У, П, Ч, Ь, Ъ, Ы, Я?
Решение: Третья сторона треугольника
должна быть больше разности
двух других сторон (чем3-1=2)
и меньше суммы этих
сторон (чем 3+1=4).
Это натуральное
число 3.
буквы симметричны относительно вертикальной оси;
буквы симметричны относительно горизонтальной оси;
буквы симметричны относительно обеих осей;
буквы не имеют осей симметрии.
Задача 2.
Периметр треугольника
равен 7 дм.
Слайд 14Ребро куба.
Четыре треугольника.
Имеется куб, который содержит столько же кубических сантиметров,
всей его поверхности.
Какая длина ребра у этого куба?
Как из шести спичек, не ломая их,
сложить четыре треугольника,
каждая сторона которых
равна одной спичке?
Решение:
Из шести спичек составляется правильная треугольная пирамида.
Ответ: длина ребра 6.
Слайд 15
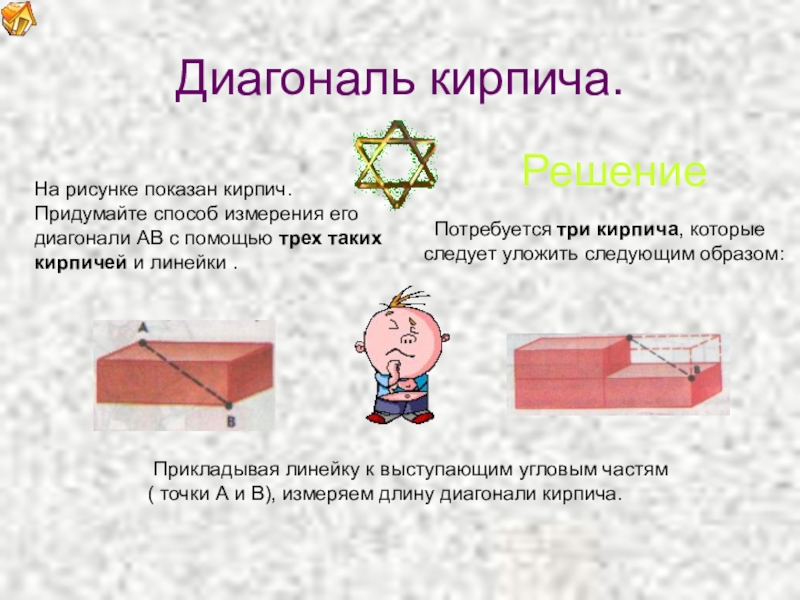
На рисунке показан кирпич. Придумайте способ измерения его диагонали
Решение
Потребуется три кирпича, которые следует уложить следующим образом:
Прикладывая линейку к выступающим угловым частям ( точки А и В), измеряем длину диагонали кирпича.
Диагональ кирпича.
Слайд 16
Требуется построить ломаную из четырех звеньев, проходящую через
Решение
Комментарий: Часто мы не можем найти решение потому, что наш разум замыкается в площади рисунка. А нигде не сказано о том, что за его пределы выходить нельзя.
Вывод: Для того чтобы понять систему, надо… из нее выйти.
Девять точек.
Слайд 17
В одной сказке хозяин, нанимая работника, предложил ему
- Вот тебе бочка, наполни ее водой ровно наполовину, ни больше, ни меньше. Но смотри, палкой, веревкой или чем-либо другим для измерения не пользуйся.
Работник справился с заданием. Как он это сделал?
Решение
Если вода в бочке налита ровно наполовину, то, наклонив бочку так, чтобы уровень воды пришелся как раз
у края бочки, мы увидим, что высшая точка дна находится также на уровне воды. Это потому, что плоскость, проведенная через диаметрально противоположные точки верхней и нижней окружностей бочки, делит ее
на две равные части.
ровно наполовину меньше больше половины
Бочка наполовину.
Слайд 18
Решение
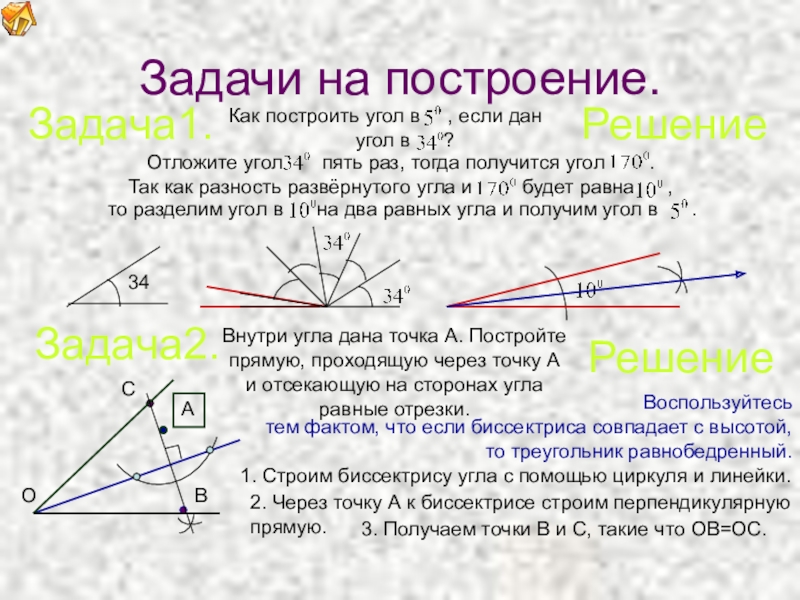
Задачи на построение.
Как построить угол в
угол в ?
Отложите угол пять раз, тогда получится угол .
Так как разность развёрнутого угла и будет равна ,
Задача1.
то разделим угол в на два равных угла и получим угол в .
Задача2.
Решение
Внутри угла дана точка А. Постройте
прямую, проходящую через точку А
и отсекающую на сторонах угла
равные отрезки.
О
В
Воспользуйтесь
тем фактом, что если биссектриса совпадает с высотой,
то треугольник равнобедренный.
1. Строим биссектрису угла с помощью циркуля и линейки.
2. Через точку А к биссектрисе строим перпендикулярную
прямую.
3. Получаем точки В и С, такие что ОВ=ОС.
С
Слайд 19
1. Разные способы.
Высоты треугольника АВС, проведенные из точек
Найдите угол АМС, если
Способ 1. Рассмотрим прямоугольные
Способ 2. Рассмотрим треугольник АВС.
Способ 3.
Из треугольника АВС находим
Т.к. углы КМА и АМС -смежные, то
Способ 4.
Из тр-ка АВС находим
Т.к. углы РМС и АМС -смежные, то
(сумма углов четырёхугольника)
Т.к.углы КМР и АМС –
вертикальные, то
Слайд 20
2. Разные способы.
Докажите, что треугольник, в котором медиана равна
к которой она проведена, является прямоугольным.
1способ:
При доказательстве использовались теорема о сумме углов треугольника и свойство углов при основании равнобедренного треугольника.
2способ:
В данном способе использовалась теорема
о внешнем угле треугольника, свойство
углов при основании равнобедренного тр-ка,
теорема о смежных углах.
3способ:
Равноудалённость
точек A,B,C от D
означает, что треугольник
вписан в окружность R=AD=DB=DC.
По свойству вписанного угла .
Слайд 21
Если две стороны одного треугольника
пропорциональны двум сторонам
треугольника и углы, образованные этими
сторонами равны, то треугольники подобны.
2) Смежные углы равны.
3) Медиана равнобедренного треугольника,
проведённая к его основанию, является его
высотой.
1.Тестовые вопросы.
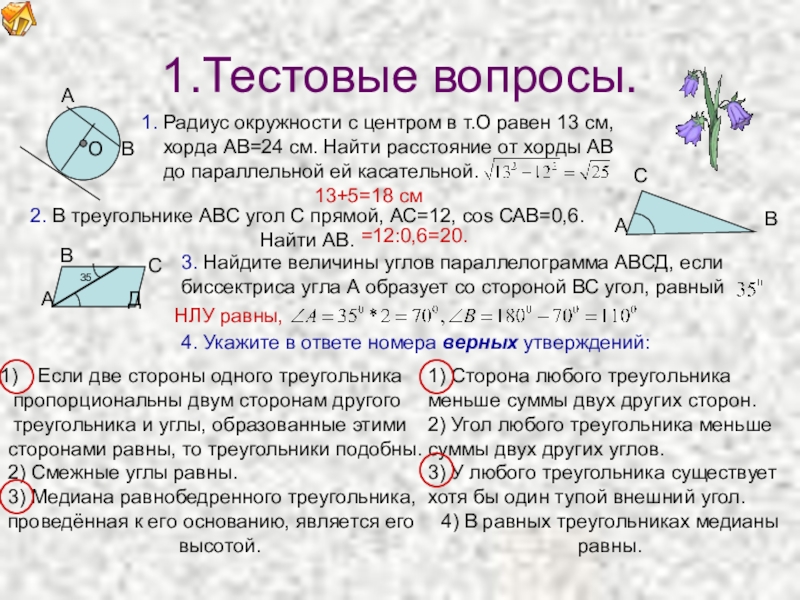
1) Сторона любого треугольника меньше суммы двух других сторон.
2) Угол любого треугольника меньше суммы двух других углов.
3) У любого треугольника существует хотя бы один тупой внешний угол.
4) В равных треугольниках медианы равны.
4. Укажите в ответе номера верных утверждений:
1. Радиус окружности с центром в т.О равен 13 см,
хорда АВ=24 см. Найти расстояние от хорды АВ
до параллельной ей касательной.
13+5=18 см
2. В треугольнике АВС угол С прямой, АС=12, cos САВ=0,6.
Найти АВ.
3. Найдите величины углов параллелограмма АВСД, если
биссектриса угла А образует со стороной ВС угол, равный
=12:0,6=20.
НЛУ равны,
Слайд 22
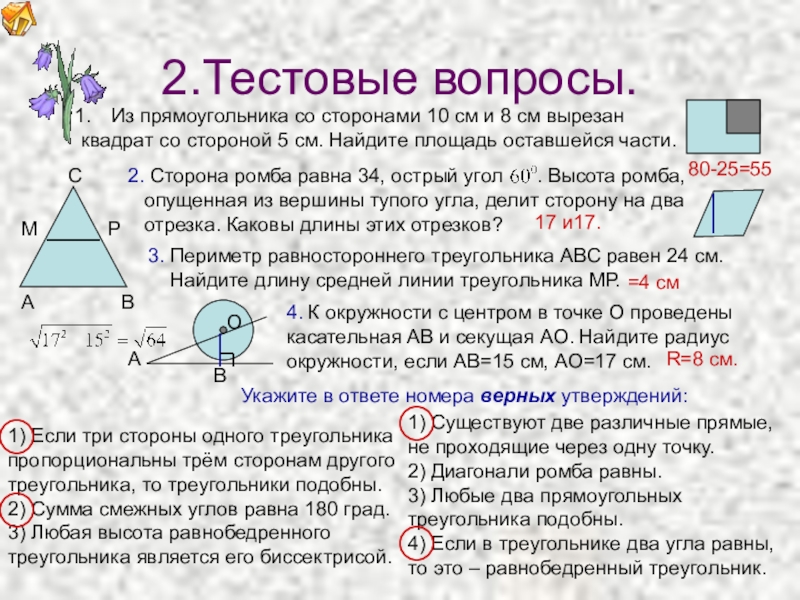
3. Периметр равностороннего треугольника АВС равен 24 см.
А
В
С
М
Р
2. Сторона ромба равна 34, острый угол . Высота ромба,
опущенная из вершины тупого угла, делит сторону на два
отрезка. Каковы длины этих отрезков?
Из прямоугольника со сторонами 10 см и 8 см вырезан
квадрат со стороной 5 см. Найдите площадь оставшейся части.
17 и17.
=4 см
1) Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.
2) Сумма смежных углов равна 180 град.
3) Любая высота равнобедренного треугольника является его биссектрисой.
1) Существуют две различные прямые, не проходящие через одну точку.
2) Диагонали ромба равны.
3) Любые два прямоугольных треугольника подобны.
4) Если в треугольнике два угла равны, то это – равнобедренный треугольник.
4. К окружности с центром в точке О проведены
касательная АВ и секущая АО. Найдите радиус
окружности, если АВ=15 см, АО=17 см.
R=8 см.
Укажите в ответе номера верных утверждений:
2.Тестовые вопросы.
80-25=55
Слайд 23
3.Тестовые вопросы.
1) Существует треугольник, сторона которого равна сумме
2) Существует треугольник, угол которого равен сумме двух других углов.
3) Любой треугольник имеет не менее двух тупых внешних углов.
4) В равных треугольниках высоты равны.
1)Через точку, не лежащую на данной прямой, можно провести прямую,
параллельную этой прямой.
2)Треугольник со сторонами 1, 2, 4 существует.
3)Если в ромбе один из углов равен 90, то такой ромб — квадрат.
5. Укажите в ответе номера верных утверждений:
4. В угол С величиной вписана окружность, которая
касается сторон угла в т.А и В.Найти величину угла АОС.
3. Основания трапеции 4 и 10 см. Диагональ трапеции делит среднюю
линию на два отрезка. Найдите длину большего из них.
2. Углы, отмеченные на рисунке одной дугой, равны.
Найдите угол .
1. Сколько осей симметрии имеет фигура?
10:2=5 см
пять
Слайд 24
4.Тестовые вопросы.
1) Центром симметрии квадрата является точка
2) Если две стороны треугольника равны
3 и 5, то его третья сторона больше 2.
3) Если в четырехугольнике две стороны параллельны, то этот четырехугольник—параллелограмм.
1) Если два угла одного треугольника равны двум углам другого
треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
Укажите в ответе номера верных утверждений:
1. Радиус окружности ОВ пересекает хорду МР в её
середине-точке К. Найдите длину хорды МР, если
КВ=1 см, радиус окружности 13 см.
МР=2МК=10 см.
2. Прямые m и n параллельны. Найдите угол 3, если
3. Средняя линия трапеции равна 11, меньшее основание
равно 5. Найдите большее основание трапеции.
2*11-5=17.
Слайд 25
5.Тестовые вопросы.
1) Если радиус круга равен 4, то
2) Любой равнобедренный треугольник имеет не менее одной оси симметрии.
3) Если угол одного треугольника равен
углу другого треугольника, то такие
треугольники подобны.
1) Площадь прямоугольного треугольника равна произведению его катетов.
2) В подобных треугольниках соответствующие углы равны.
3) В прямоугольном треугольнике катет, лежащий против угла в 30° равен
половине гипотенузы.
1. Укажите номера верных утверждений:
2. Найдите площадь треугольника, изображенного
на рисунке.
3. Сторона ромба равна 20,а острый угол равен . Найдите
длину меньшей диагонали.
4. В окружности с центром О проведены диаметры АД и ВС.
Центральный угол АОС равен 112 град. Найдите вписанный
угол АДВ.
S=(15+6)*8:2=84
d=20
Слайд 26
6.Тестовые вопросы.
1) Если один из углов равнобедренного треугольника
его угол равен .
2) Если два треугольника подобны, то их соответствующие стороны равны.
3) Если основания трапеции равны 2 и 8, то средняя линия этой трапеции
равна 5.
1) тангенсом острого угла прямоугольного треугольника называется
отношение прилежащего катета к противолежащему катету;
2) ромб, диагонали которого равны, является квадратом;
3) противоположные углы параллелограмма равны между собой;
Укажите номера верных утверждений:
1. Точки А и В делят окружность на две дуги, длины
которых относятся как 9:11. Найдите величину центрального угла,
опирающегося на меньшую из дуг.
3. Найдите площадь треугольника, если высота, проведенная
к одной из ее сторон, равна 11, а средняя линия, параллельная
этой стороне, равна 10.
2. Какой угол(в градусах) образуют минутная и часовая стрелки,
когда часы показывают ровно 4 часа.
S=11*10=110
Слайд 27
7.Тестовые вопросы.
1) ромб, диагонали которого равны, является квадратом;
2) противоположные углы параллелограмма равны между собой;
3) котангенсом острого угла прямоугольного треугольника называется
отношение прилежащего катета
к противолежащему катету.
1) Вертикальные углы равны.
2) Площадь прямоугольного треугольника равна произведению
двух его катетов.
3) В равнобедренном треугольнике высота является медианой и
биссектрисой.
4) Через любые две точки проходит прямая и притом только одна.
1. Укажите номера верных утверждений.
2. В ромбе ABCD известны диагонали AC=6 и BD=8. Найдите
длину вектора .
3. Гипотенуза равнобедренного прямоугольного треугольника
равна . Найдите площадь треугольника.
4. В четырехугольнике ABCD AB=7, BС=13 и СD=11. Найдите
четвертую сторону четырехугольника, если в него можно вписать окружность.
АВ+СД=ВС+АД,
АД=(7+11)-13=5.
Слайд 28
8.Тестовые вопросы.
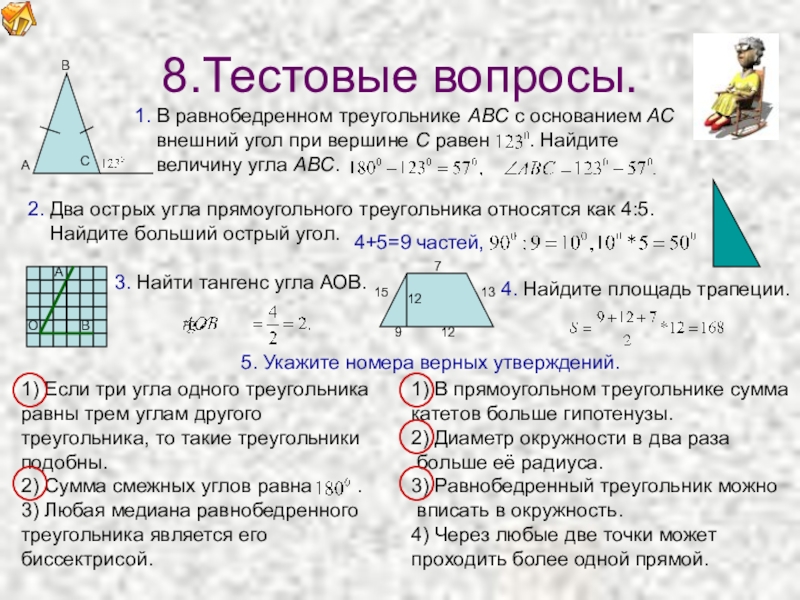
1) В прямоугольном треугольнике сумма
катетов больше гипотенузы.
2) Диаметр окружности
больше её радиуса.
3) Равнобедренный треугольник можно
вписать в окружность.
4) Через любые две точки может
проходить более одной прямой.
5. Укажите номера верных утверждений.
1) Если три угла одного треугольника равны трем углам другого
треугольника, то такие треугольники подобны.
2) Сумма смежных углов равна .
3) Любая медиана равнобедренного треугольника является его
биссектрисой.
1. В равнобедренном треугольнике ABC с основанием AC
внешний угол при вершине C равен . Найдите
величину угла ABC.
4. Найдите площадь трапеции.
3. Найти тангенс угла АОВ.
2. Два острых угла прямоугольного треугольника относятся как 4:5.
Найдите больший острый угол.
4+5=9 частей,
Слайд 29
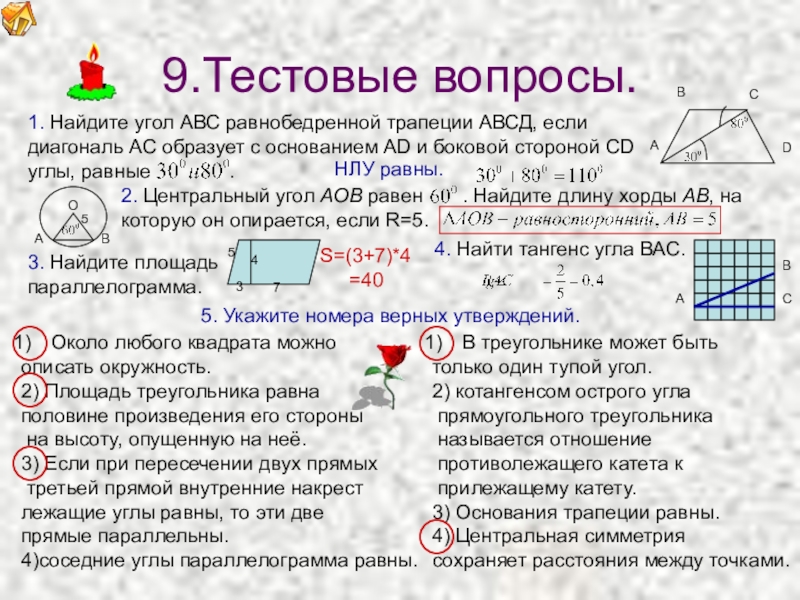
Около любого квадрата можно
описать окружность.
2) Площадь треугольника
половине произведения его стороны
на высоту, опущенную на неё.
3) Если при пересечении двух прямых
третьей прямой внутренние накрест
лежащие углы равны, то эти две
прямые параллельны.
4)соседние углы параллелограмма равны.
9.Тестовые вопросы.
В треугольнике может быть
только один тупой угол.
2) котангенсом острого угла
прямоугольного треугольника
называется отношение
противолежащего катета к
прилежащему катету.
3) Основания трапеции равны.
4) Центральная симметрия
сохраняет расстояния между точками.
5. Укажите номера верных утверждений.
1. Найдите угол АВС равнобедренной трапеции АВСД, если
диагональ АС образует с основанием AD и боковой стороной CD
углы, равные .
2. Центральный угол AOB равен . Найдите длину хорды AB, на которую он опирается, если R=5.
4. Найти тангенс угла ВАС.
3. Найдите площадь
параллелограмма.
НЛУ равны.
S=(3+7)*4
=40
Слайд 30
10.Тестовые вопросы.
1) Смежные углы равны.
2) Площадь прямоугольника
3) Существует треугольник, высота которого совпадает с его меньшей
стороной.
4) Через любые две точки может проходить более одной прямой.
1) Если вписанный угол равен 58◦, то центральный угол, опирающийся
на ту же дугу окружности, равен 116◦.
2)Около любого ромба можно описать окружность.
3)В треугольнике ABC, для которого
AB =6, BC =8, AC =11, угол
при вершине C – наименьший.
1. Укажите номера верных утверждений.
2. В треугольнике ABC ,BD -биссектриса. Найдите угол ADB.
3. Найдите площадь четырёхугольника, изображённого на рисунке.
Диагонали четырёхугольника перпендикулярны.
4. Найдите косинус
угла АВС.
5. Найдите угол ДОС, если угол АОВ -развёрнутый.
Угол АДВ -внешний,
S=(5+2)*(3+8):2=38,5
Слайд 31
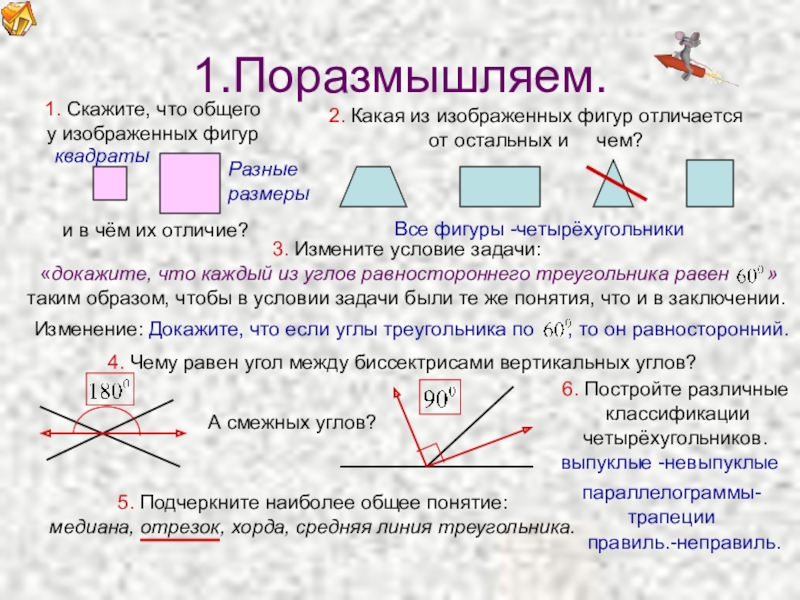
1.Поразмышляем.
4. Чему равен угол между биссектрисами вертикальных углов?
3.
«докажите, что каждый из углов равностороннего треугольника равен »
таким образом, чтобы в условии задачи были те же понятия, что и в заключении.
Изменение: Докажите, что если углы треугольника по , то он равносторонний.
5. Подчеркните наиболее общее понятие:
медиана, отрезок, хорда, средняя линия треугольника.
1. Скажите, что общего
у изображенных фигур
и в чём их отличие?
2. Какая из изображенных фигур отличается
от остальных и чем?
А смежных углов?
6. Постройте различные
классификации
четырёхугольников.
квадраты
Разные
размеры
Все фигуры -четырёхугольники
выпуклые -невыпуклые
параллелограммы-
трапеции
правиль.-неправиль.
Слайд 32
2. Выберите из 5 терминов: прямые, отрезки, лучи,
два, которые бы наиболее точно определяли понятие угол.
6. Найдите четвёртое понятие, которое бы так соотносилось с третьим понятием,
как первое со вторым: угол-вершина угла, окружность-…?
1. Подумайте, как связаны первые две фигуры и укажите из набора фигур ту,
что также связана с третьей фигурой.
3. Сравните параллелограмм и трапецию.
2.Поразмышляем.
4. Вам дано 5 спичек. Сложите из них два равносторонних
треугольника.
5. А если спичек будет 6,
то сколько равносторонних
треугольников вы
можете изобразить?
7. Выдели существенные признаки понятий
«равносторонний треугольник»,«ромб».
два
на плоскости
четыре
в пространстве
два
Центр окружности
одна пара II прямых, а не две.
равенство всех сторон
Слайд 33
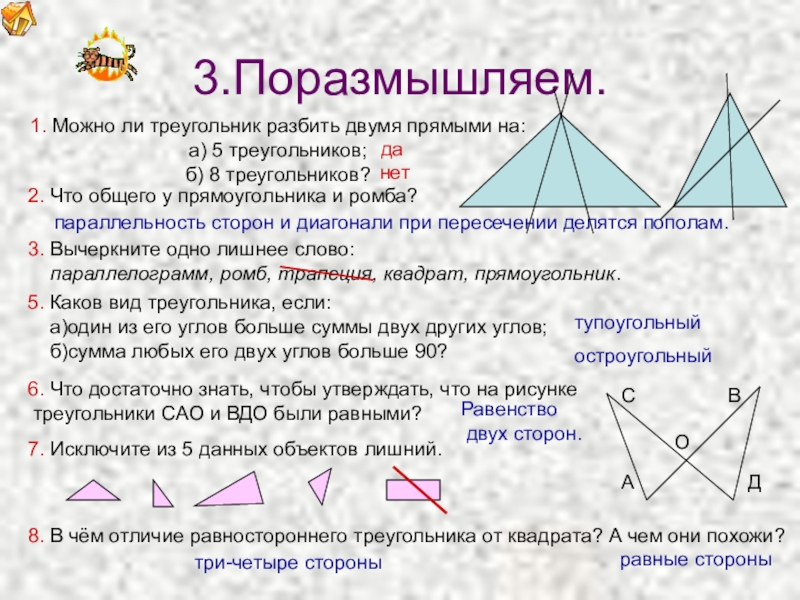
3.Поразмышляем.
1. Можно ли треугольник разбить двумя прямыми
а) 5 треугольников;
б) 8 треугольников?
5. Каков вид треугольника, если:
а)один из его углов больше суммы двух других углов;
б)сумма любых его двух углов больше 90?
тупоугольный
остроугольный
6. Что достаточно знать, чтобы утверждать, что на рисунке
треугольники САО и ВДО были равными?
3. Вычеркните одно лишнее слово:
параллелограмм, ромб, трапеция, квадрат, прямоугольник.
8. В чём отличие равностороннего треугольника от квадрата? А чем они похожи?
2. Что общего у прямоугольника и ромба?
7. Исключите из 5 данных объектов лишний.
да
нет
параллельность сторон и диагонали при пересечении делятся пополам.
Равенство
двух сторон.
три-четыре стороны
равные стороны
Слайд 34
4.Поразмышляем.
2. Может ли угол при основании равнобедренного
равняться ?
1. Сравните треугольник и тетраэдр.
Нет, т.к. в треугольнике двух тупых углов быть не может.
6. Найдите два других угла
равнобедренного треугольника,
если один из углов равен
3. Какие из следующих утверждений верны?
1) Площадь круга равна произведению длины его окружности на радиус.
2) В треугольнике АВС, для которого , сторона АВ -наибольшая.
3) Если в параллелограмме диагонали равны и перпендикулярны, то этот
параллелограмм— квадрат.
5. Найдите длину
большей высоты
параллелограмма.
4. Найдите в градусах величину
той из двух дуг AC окружности,
на которую опирается угол ABC.
Дуга, на которую опирается угол,
составляет 3/4 всей окружности.
Большая высота
опущена на меньшее
основание (2 клетки)
H=2
1 случай: угол
против основания
2 случай: угол
при основании
Слайд 35
5.Поразмышляем.
3. Найдите
2. Дан треугольник со сторонами 8 ,12 и 5. Найдите
периметр треугольника, вершинами которого
являются середины сторон данного треугольника.
5. Найдите площадь трапеции, вершины
которой имеют координаты
А(-1 ; 2), В(-1 ; 5), Д(1 ; 0), С(1 ; 6) .
1. Все фигуры, кроме одной, имеют общее свойство. Какая фигура лишняя?
Если все остальные
фигуры повернуть «вниз
головой», то они не
изменят своего положения.
4. Найдите в градусах величину
той из двух дуг AC окружности,
на которую опирается угол ABC.
Р=4+6+2,5=
=12,5
Слайд 36
6.Поразмышляем.
3. Найдите
величину
угла AВC.
4. Дан треугольник со сторонами 24
которого являются середины сторон данного треугольника.
1. Одна из фигур чем-то
отличается от остальных.
Найдите её.
Каждый треугольник можно получить один из другого поворотом, кроме четвёртой.
2. В каждый из двух квадратов вписаны окружности. Радиус одной из этих окружностей в 3 раза больше радиуса другой.
Площадь большего квадрата равна 18. Найдите площадь меньшего квадрата.
R=3r
а1= 1/3а
S1=2
Данный треугольник является прямоугольным,
т.к. катеты меньшего треугольника 5 и 12.
Угол АВС-
вписанный
Решение:
S=18
Слайд 37
7.Поразмышляем.
2. Длины двух смежных сторон параллелограмма относятся как 2:3.
Найдите
равен 30.
4. Сколько всего осей
симметрии имеет фигура?
Ответ: всего 4+4=8 осей.
3.Найдите .
1. Какая из шести фигур
должна занять свободное
место в ряду фигур?
Решение
В строке не хватает круга.
В каждом столбце затушевана одна и та же фигура.
Это кружок. Следует выбрать одну фигуру из двух.
Затушеванная фигура занимает одно из трёх
местоположений внутри фигуры. Делаем отбор.
Решение: Пусть х -одна часть,
(2х+3х)*2=30,
х=3.
Ответ: 3*3=9 большая сторона.
Слайд 38
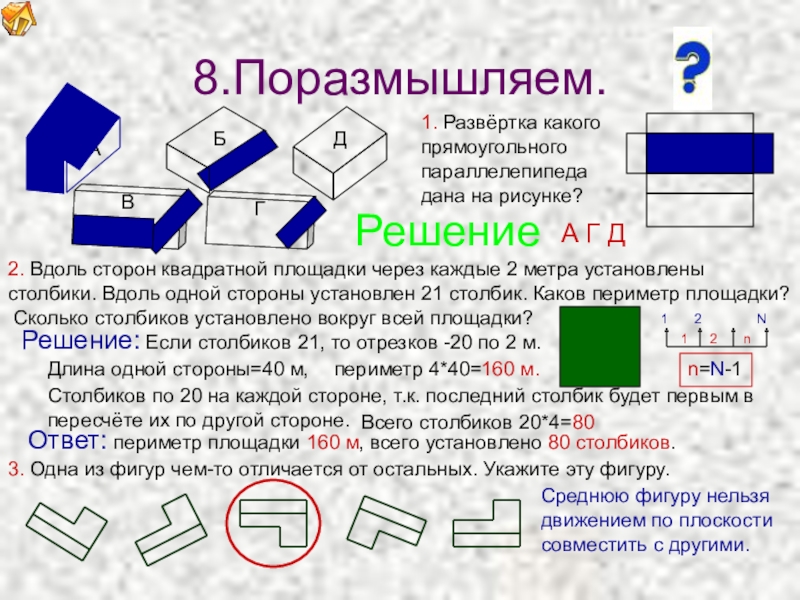
8.Поразмышляем.
Решение
1. Развёртка какого
прямоугольного
параллелепипеда
дана на рисунке?
2. Вдоль сторон квадратной
столбики. Вдоль одной стороны установлен 21 столбик. Каков периметр площадки?
Сколько столбиков установлено вокруг всей площадки?
Ответ: периметр площадки 160 м, всего установлено 80 столбиков.
Решение: Если столбиков 21, то отрезков -20 по 2 м.
периметр 4*40=160 м.
Длина одной стороны=40 м,
Столбиков по 20 на каждой стороне, т.к. последний столбик будет первым в
пересчёте их по другой стороне.
3. Одна из фигур чем-то отличается от остальных. Укажите эту фигуру.
А Г Д
Среднюю фигуру нельзя
движением по плоскости
совместить с другими.
Всего столбиков 20*4=80
Слайд 39
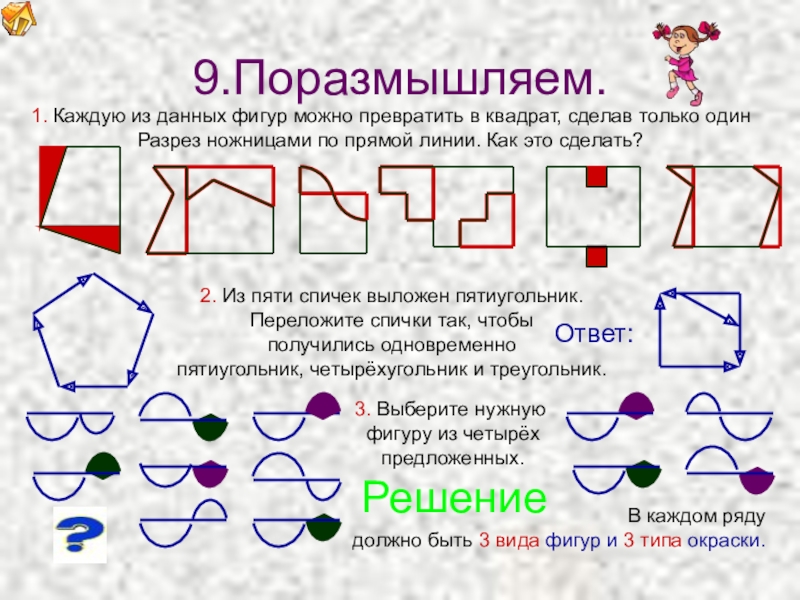
9.Поразмышляем.
Решение
1. Каждую из данных фигур можно превратить в квадрат, сделав только
Разрез ножницами по прямой линии. Как это сделать?
2. Из пяти спичек выложен пятиугольник.
Переложите спички так, чтобы
получились одновременно
пятиугольник, четырёхугольник и треугольник.
3. Выберите нужную
фигуру из четырёх
предложенных.
В каждом ряду
должно быть 3 вида фигур и 3 типа окраски.
Ответ:
Слайд 40
10.Поразмышляем.
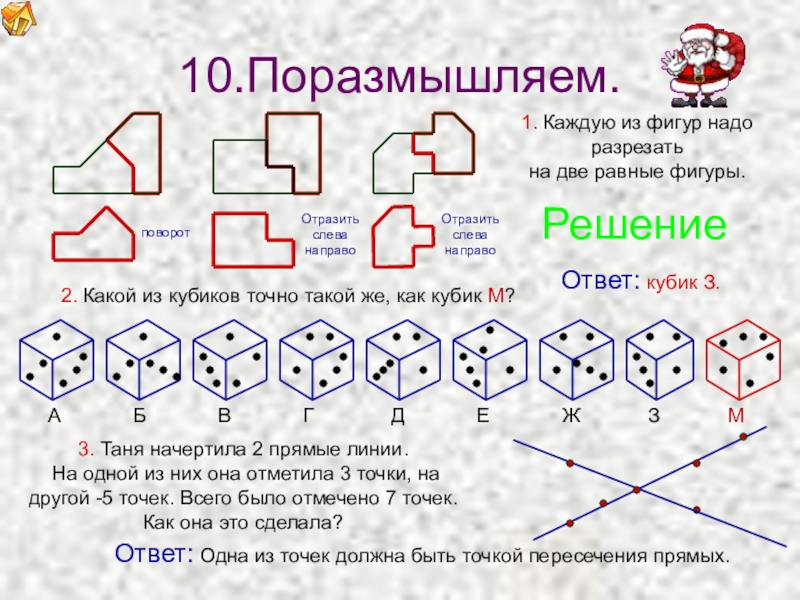
1. Каждую из фигур надо
разрезать
на две равные фигуры.
Решение
Отразить
слева
направо
Отразить
слева
направо
поворот
2. Какой
Ответ: кубик З.
А Б В Г Д Е Ж З М
3. Таня начертила 2 прямые линии.
На одной из них она отметила 3 точки, на другой -5 точек. Всего было отмечено 7 точек.
Как она это сделала?
Ответ: Одна из точек должна быть точкой пересечения прямых.
Слайд 41Тест1. Выбор ответов.
В 11. Укажите номера верных утверждений:
1) У выпуклого многоугольника
углов.
2) Не существует выпуклого многоугольника, имеющего ровно 10
диагоналей.
3) Существует четырехугольник, который можно разрезать двумя
прямыми на шесть частей.
4) Если в выпуклом четырехугольнике диагонали равны, и хотя бы
один из углов равен 90 , то этот четырехугольник – прямоугольник.
5) Если диагонали четырехугольника взаимно перпендикулярны и
имеют общую середину, то этот четырехугольник – ромб.
Ответы: 1235
но 4 острых меньше, чем 4*90=360.
1.Сумма всех углов выпуклого многоугольника
Значит, д.б.
2.Количество диагоналей многоугольника
вычисляется по формуле
Уравнение не имеет целых корней.
3.
4.
Слайд 42Тест2. Выбор ответов.
В 11. Укажите номера верных утверждений:
1) Если не все
2) Не существует многоугольника, у которого число диагоналей равно числу его сторон.
3) Существует пятиугольник, который можно разрезать по прямой на два треугольника.
4) Если в выпуклом четырехугольнике две противоположные стороны равны, а две другие параллельны, то этот четырехугольник - параллелограмм.
5) Если диагонали четырехугольника равны и взаимно перпендикулярны, то этот четырехугольник – квадрат.
Ответы: 13
4. Это м.б.
равнобокая
трапеция.
1. Сумма всех углов выпуклого многоугольника
равна 180 градусам. Двух тупых быть не может,
а также все острые не м.б. т.к.будет .
Не может быть также и три острых и прямой.
2. Количество всех диагоналей многоугольника
вычисляется по формуле .
Уравнение имеет корень = 5.
3.
5.