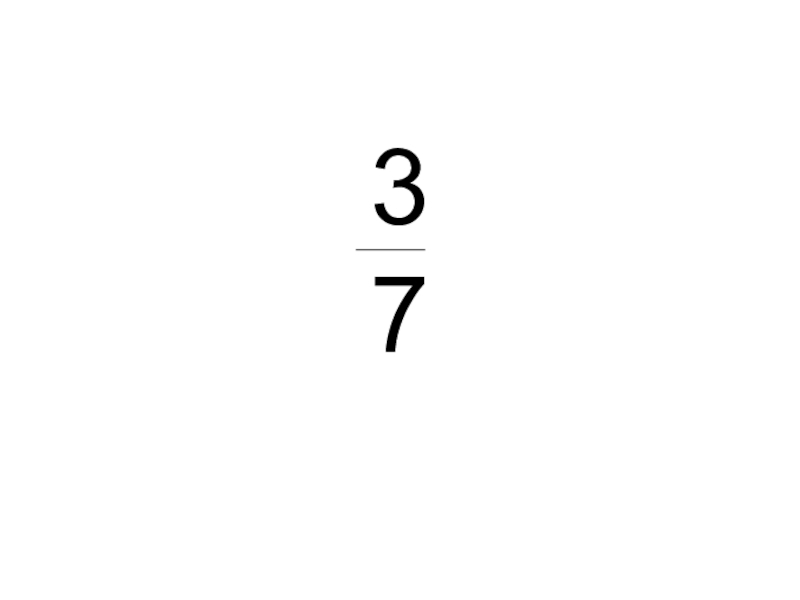- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Особенности преподавания математики с использованием проблемных технологий
Содержание
- 1. Особенности преподавания математики с использованием проблемных технологий
- 2. Проблемы:проблема несоответствия уровня обученности школьников их реальным
- 3. Предмет математики настолько серьёзен, что нужно не упускать возможность делать его немного занимательным. Паскаль.
- 4. Под проблемным обучением понимается такая организация учебных
- 5. Технологию проблемного обучения использую в основном на
- 6. Данная технология позволяет:активизировать познавательную деятельность учащихся на
- 7. Магия фокуса способна разбудить сонных, растормошить ленивых,
- 8. 9595 9595раздели371337ФокусЧисло Шехерезады
- 9. Секрет фокуса: если к любому трехзначному числуПриписать
- 10. Слайд 10
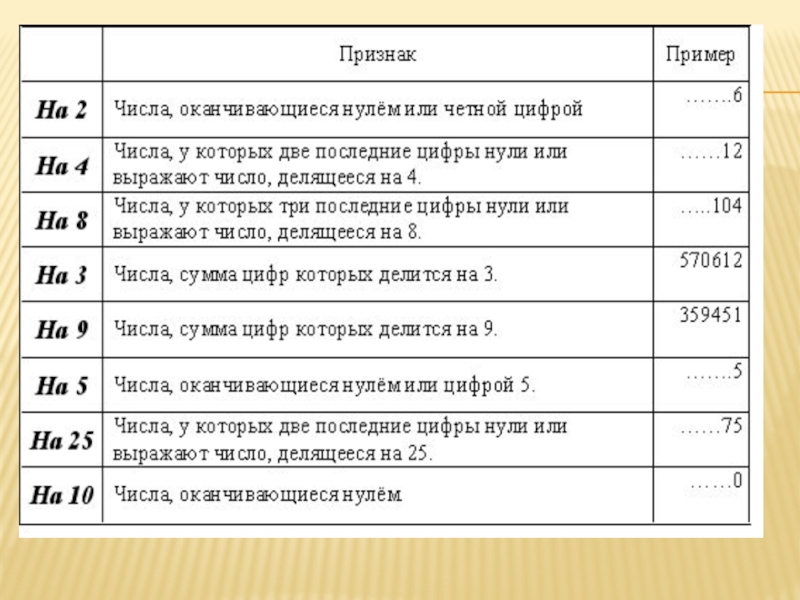
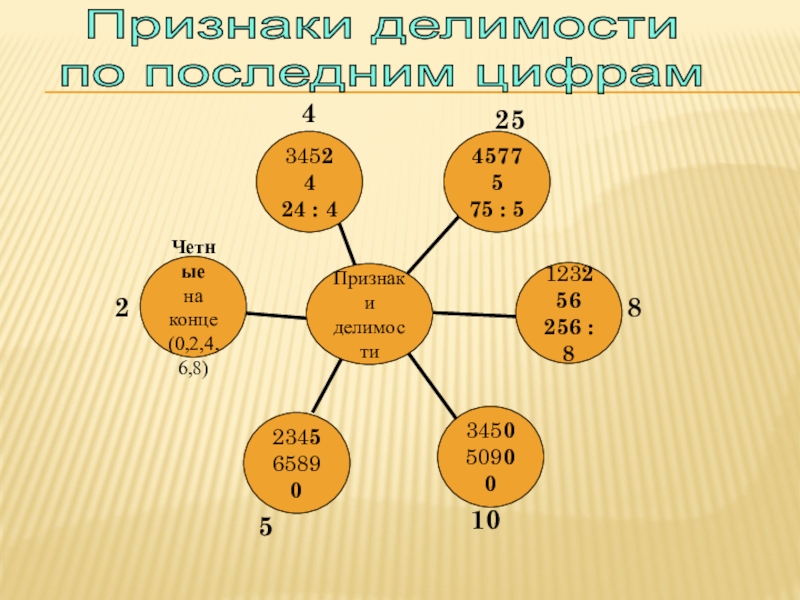
- 11. 4Признаки делимости по последним цифрам
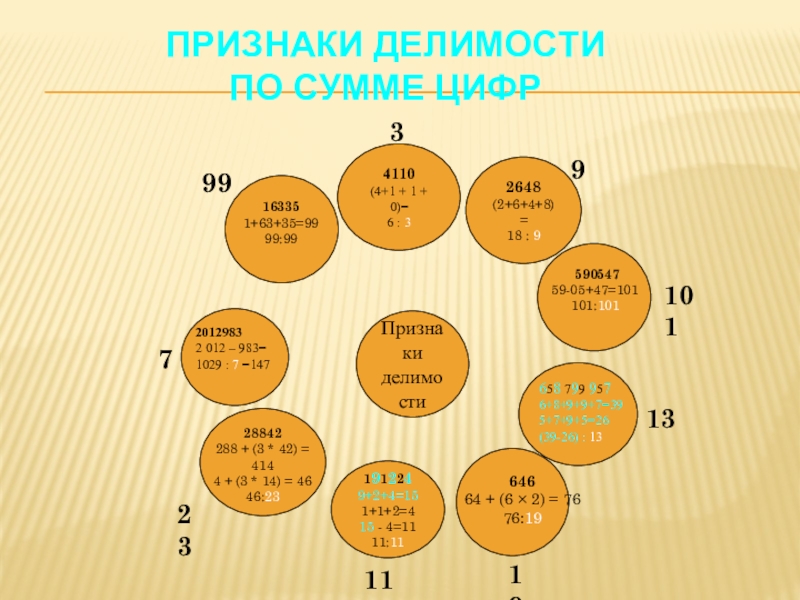
- 12. Признаки делимости по сумме цифр 193
- 13. Признаки делимости на составное число
- 14. Виды проблемных заданийНа уроках я использую следующие
- 15. Примеры.1. Тема «Проценты». В конкурсе участвовали два класса. Из
- 16. Типология познавательных задач.1. Задачи с несформулированным вопросом.Пример. Шоколад
- 17. 2. Задачи с недостающими данными.Пример. Из двух пунктов
- 18. 3. Задачи с излишними данными.Пример. Масса 11 ящиков
- 19. 4. Задачи с несколькими решениями.Пример. За три дня
- 20. 5. Задачи с меняющимся содержанием.Пример. Исходная задача. Туристы
- 21. Создание проблемных ситуацийЗадание. Как вы полагаете, верно ли выполнено сравнение? 24, 325 < 24, 4
- 22. Заключение Достаточно много времени тратится и
- 23. Спасибо за внимание!!!
Проблемы:проблема несоответствия уровня обученности школьников их реальным возможностям;- низкий уровень мотивации;снижение или отсутствие интереса к предмету;- высокий уровень тревожности учащихся;быстрая утомляемость на уроках и, какследствие, перегрузка учащихся, ухудшение их здоровья.
Слайд 2Проблемы:
проблема несоответствия уровня обученности
школьников их реальным возможностям;
- низкий уровень мотивации;
снижение
или отсутствие интереса к
предмету;
- высокий уровень тревожности учащихся;
быстрая утомляемость на уроках и, как
следствие, перегрузка учащихся,
ухудшение их здоровья.
предмету;
- высокий уровень тревожности учащихся;
быстрая утомляемость на уроках и, как
следствие, перегрузка учащихся,
ухудшение их здоровья.
Слайд 3Предмет математики настолько серьёзен, что нужно не упускать возможность делать его
немного занимательным.
Паскаль.
Слайд 4
Под проблемным обучением понимается такая организация учебных занятий, которая предполагает создание
под руководством учителя проблемных ситуаций и активную самостоятельную деятельность учащихся по их разрешению, в результате чего и
происходит творческое овладение знаниями, умениями, навыками.
происходит творческое овладение знаниями, умениями, навыками.
.
Слайд 5Технологию проблемного обучения
использую в основном на уроках:
изучения нового материала и
первичного закрепления;
комбинированных;
- блоковых проблемных занятиях - тренингах.
комбинированных;
- блоковых проблемных занятиях - тренингах.
Слайд 6Данная технология позволяет:
активизировать познавательную деятельность
учащихся на уроке, что позволяет справляться
с
большим объемом учебного материала;
сформировать стойкую учебную мотивацию,
а учение с увлечением – это яркий пример
здоровьесбережения;
использовать полученные навыки организации
самостоятельной работы для получения новых
знаний из разных источников информации;
повысить самооценку учащихся, т. к. при
решении проблемы выслушиваются
и принимаются во внимание любые мнения.
большим объемом учебного материала;
сформировать стойкую учебную мотивацию,
а учение с увлечением – это яркий пример
здоровьесбережения;
использовать полученные навыки организации
самостоятельной работы для получения новых
знаний из разных источников информации;
повысить самооценку учащихся, т. к. при
решении проблемы выслушиваются
и принимаются во внимание любые мнения.
Слайд 7Магия фокуса способна разбудить сонных, растормошить ленивых, заставить думать тугодумов. Ведь
не разгадав секрета фокуса, невозможно понять и оценить всей его прелести. А секрет фокуса чаще всего имеет математическую природу.
Слайд 9Секрет фокуса:
если к любому трехзначному числу
Приписать справа такое же число,
то трехзначное число при этом увеличится в 1001 раз.
Число 1001 равно произведению чисел 7, 11,13 поэтому после деления мы и получаем задуманное число.
При повторении фокуса можно внести в него некоторое разнообразие, обращаясь каждый раз к новым делителям. А именно, вместо четырех множителей 3•7•13•37, можете взять следующие группы трех множителей: 21•13•37; 7•39•37; 3•91•37; 7•13•111.
Число 1001 равно произведению чисел 7, 11,13 поэтому после деления мы и получаем задуманное число.
При повторении фокуса можно внести в него некоторое разнообразие, обращаясь каждый раз к новым делителям. А именно, вместо четырех множителей 3•7•13•37, можете взять следующие группы трех множителей: 21•13•37; 7•39•37; 3•91•37; 7•13•111.
Слайд 14Виды проблемных заданий
На уроках я использую следующие виды
проблемных заданий:
1. Разрыв причинно
– следственных связей.
2. Подход к расположению фраз
(с известного факта). «Известно, что…».
3. «Как объяснить тот факт, что …».
4. Проблемное задание на предположение.
«Как вы полагаете …».
5. Точки зрения ученых, историков.
6. Конкретный пример, который нужно
подтвердить или опровергнуть.
2. Подход к расположению фраз
(с известного факта). «Известно, что…».
3. «Как объяснить тот факт, что …».
4. Проблемное задание на предположение.
«Как вы полагаете …».
5. Точки зрения ученых, историков.
6. Конкретный пример, который нужно
подтвердить или опровергнуть.
Слайд 15Примеры.
1. Тема «Проценты».
В конкурсе участвовали два класса.
Из 5 «а» класса –
50% учащихся, а из 5 «б» - 40%.
При подсчете оказалось, что количество участников
из каждого класса одинаково. Почему?
2. Тема «Свойства деления»
Коле дали задание найти значение выражения
(37 + 34*5) : (45*3 – 135) .
Он сказал, что найти значение этого
выражения нельзя. Прав ли он?
При подсчете оказалось, что количество участников
из каждого класса одинаково. Почему?
2. Тема «Свойства деления»
Коле дали задание найти значение выражения
(37 + 34*5) : (45*3 – 135) .
Он сказал, что найти значение этого
выражения нельзя. Прав ли он?
Слайд 16Типология познавательных задач.
1. Задачи с несформулированным вопросом.
Пример. Шоколад стоит 15 руб., коробка
конфет 30 руб. Задайте все возможные
вопросы по условию данной задачи.
Слайд 17
2. Задачи с недостающими данными.
Пример. Из двух пунктов вышли
одновременно навстречу друг
другу два
пешехода.
Скорость одного пешехода равна 7 км/ч,
а скорость другого – на 1 км/ч больше.
Какое расстояние будет между пешеходами
через 2 часа?
пешехода.
Скорость одного пешехода равна 7 км/ч,
а скорость другого – на 1 км/ч больше.
Какое расстояние будет между пешеходами
через 2 часа?
Слайд 18
3. Задачи с излишними данными.
Пример. Масса 11 ящиков яблок 4 ц 62 кг,
а масса 18 ящиков груш 6 ц 12 кг.
В магазин привезли 22 ящика яблок
и 6 ящиков груш.
На сколько килограммов масса одного
ящика яблок больше
массы одного ящика груш.
Слайд 19
4. Задачи с несколькими решениями.
Пример. За три дня в магазине продано
1280 кг яблок.
В первый день продали 25% всех яблок,
а во второй день – 45% всех яблок.
Сколько килограммов яблок продали в
третий день?
Решите задачу несколькими способами.
Какой из них наиболее простой.
а во второй день – 45% всех яблок.
Сколько килограммов яблок продали в
третий день?
Решите задачу несколькими способами.
Какой из них наиболее простой.
Слайд 205. Задачи с меняющимся содержанием.
Пример. Исходная задача.
Туристы прошли за день 20 км,
что составило 40% намеченного маршрута.
Какова длина маршрута?
Второй вариант. Туристы прошли за день 20 км,
и им осталось пройти 60% намеченного
маршрута.
Какова длина маршрута?
Слайд 21Создание проблемных ситуаций
Задание.
Как вы полагаете, верно ли
выполнено сравнение?
24,
325 < 24, 4
Слайд 22Заключение
Достаточно много времени тратится и на уроке на разрешение той
или иной проблемы, но это время более ценно по сравнению с тем, которое тратилось бы на подачу готовых знаний.
В этом и есть отличие современного урока.
В этом и есть отличие современного урока.