- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Особенности деятельности учителя математики по сопровождению детей с высоким потенциалом развития
Содержание
- 1. Особенности деятельности учителя математики по сопровождению детей с высоким потенциалом развития
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. Олимпиады школьников
- 6. «Математика – наука молодых. Иначе и не
- 7. Тематика заданий выбирается исходя из списка вопросов,
- 8. 7 классЗадачи на проценты (банковские проценты). Числовой
- 9. Рекомендации авторам заданий
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Принципы решения нестандартных задач по математикепреобразовать задачу
- 17. Слайд 17
- 18. 7 баллов – задача решена правильно;6 баллов
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Сайт УЧИ.РУ
- 35. Слайд 35
- 36. При подготовке ко всем этапам всероссийской олимпиады
- 37. Агаханов Н.Х., Подлипский О.К. Математика. Всероссийские олимпиады.
- 38. Андреева А.Н. ,Барабанов А.И., Чернявский И.Я. Саратовские
- 39. Гордин Р.К. Это должен знать каждый матшкольник
- 40. Кордемский Б.А. Математическая смекалка. – М., ГИФМЛ,
- 41. Домашние олимпиады
- 42. Слайд 42
- 43. Слайд 43
- 44. Олимпиадные задания прошлых лет
- 45. Примеры заданий
- 46. Слайд 46
- 47. Слайд 47
- 48. Слайд 48
- 49. Слайд 49
- 50. Слайд 50
- 51. Слайд 51
- 52. 6 класс
- 53. Слайд 53
- 54. Слайд 54
- 55. Слайд 55
Олимпиады школьников
Слайд 1Особенности деятельности учителя математики по сопровождению детей с высоким потенциалом развития
Слайд 6«Математика – наука молодых. Иначе и не может быть. Занятия математикой
– это такая гимнастика ума, для которой нужны вся гибкость и вся выносливость молодости.»
Норберт Винер
Норберт Винер
Слайд 7Тематика заданий
выбирается исходя из списка вопросов, рекомендуемых центральной предметно-методической комиссией
всероссийской олимпиады школьников по математике:
Например, 4-6 класс
задачи по арифметике,
логические задачи,
задачи по наглядной геометрии,
задачи, использующие понятие четности.
Например, 4-6 класс
задачи по арифметике,
логические задачи,
задачи по наглядной геометрии,
задачи, использующие понятие четности.
Слайд 87 класс
Задачи на проценты (банковские проценты). Числовой ребус (задачи - шутки).
Конструктивные задачи на переливания, взвешивания. Делимость натуральных чисел (признаки делимости). Задачи на разрезание и раскрашивание, геометрические головоломки. Задачи на перебор вариантов.
8 класс
Делимость натуральных чисел (признаки делимости, основная теорема арифметики). Треугольник (замечательные линии и точки треугольника). Преобразование алгебраических выражений. Построение графиков функций. Логические задачи.
9 класс
Делимость натуральных чисел, признаки делимости. Квадратный трехчлен и его свойства, решение неравенств. Текстовые задачи на составление уравнений или систем уравнений. Подобие фигур, вычисление площадей. Вероятность и статистика (перебор вариантов).
10 класс
Свойства квадратичной функции, решение неравенств. Окружность, описанные многоугольники. Делимость и остатки. Прогрессии. Вероятность и статистика.
11 класс
Делимость, остатки, четность. Задачи на многочлены (теорема Виета, теорема Безу). Тригонометрические уравнения, неравенства. Стереометрия. Вероятность и статистика.
8 класс
Делимость натуральных чисел (признаки делимости, основная теорема арифметики). Треугольник (замечательные линии и точки треугольника). Преобразование алгебраических выражений. Построение графиков функций. Логические задачи.
9 класс
Делимость натуральных чисел, признаки делимости. Квадратный трехчлен и его свойства, решение неравенств. Текстовые задачи на составление уравнений или систем уравнений. Подобие фигур, вычисление площадей. Вероятность и статистика (перебор вариантов).
10 класс
Свойства квадратичной функции, решение неравенств. Окружность, описанные многоугольники. Делимость и остатки. Прогрессии. Вероятность и статистика.
11 класс
Делимость, остатки, четность. Задачи на многочлены (теорема Виета, теорема Безу). Тригонометрические уравнения, неравенства. Стереометрия. Вероятность и статистика.
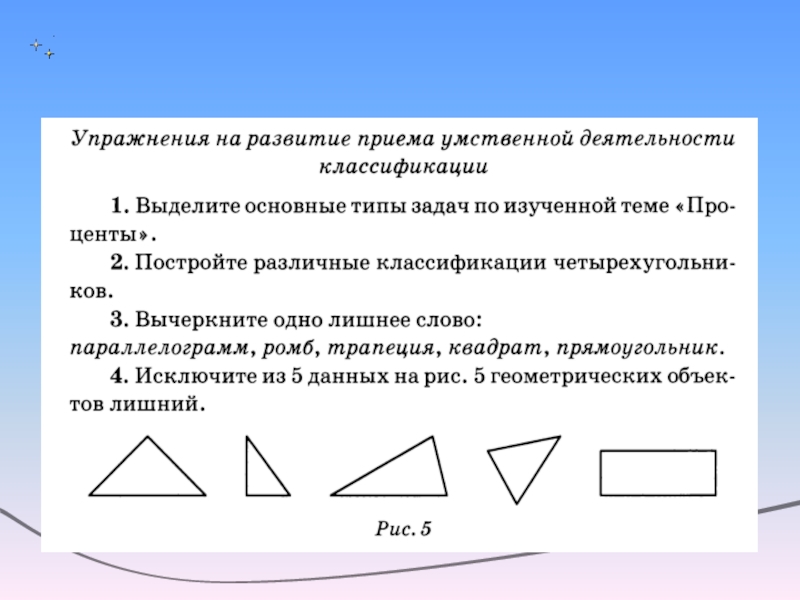
Слайд 16Принципы решения нестандартных задач по математике
преобразовать задачу к виду, удобному для
решения;
решить задачу для частного, наиболее простого случая, а затем обобщить идею решения;
предположить, что утверждение задачи – ложное; если из этого предположения получим противоречие, то утверждение задачи верно – доказательство от противного;
разбить задачу на несколько простых подзадач;
обобщить задачу; часто исследования более общей проблемы требует меньших усилий, чем исследование её частного случая – «парадокс изобретателя».
решить задачу для частного, наиболее простого случая, а затем обобщить идею решения;
предположить, что утверждение задачи – ложное; если из этого предположения получим противоречие, то утверждение задачи верно – доказательство от противного;
разбить задачу на несколько простых подзадач;
обобщить задачу; часто исследования более общей проблемы требует меньших усилий, чем исследование её частного случая – «парадокс изобретателя».
Слайд 187 баллов – задача решена правильно;
6 баллов – задача решена, но
есть мелкие замечания к решению (например, не рассмотрены некоторые простые частные случаи);
5 баллов – задача решена в целом, недостатки решения легко устраняются;
3-4 балла – задача решена «наполовину», т.е. ход решения правильный, есть значительный прогресс в решении, но полное решение требует дополнительных существенных идей;
1-2 балла – задача не решена, но подход к решению правильный или задача решена для простых частных случаев;
0 баллов – решение задачи неправильное и не содержит идей с помощью которых задача может быть решена, или задача не решалась.
5 баллов – задача решена в целом, недостатки решения легко устраняются;
3-4 балла – задача решена «наполовину», т.е. ход решения правильный, есть значительный прогресс в решении, но полное решение требует дополнительных существенных идей;
1-2 балла – задача не решена, но подход к решению правильный или задача решена для простых частных случаев;
0 баллов – решение задачи неправильное и не содержит идей с помощью которых задача может быть решена, или задача не решалась.
Критерии оценивания олимпиадных работ
Слайд 36При подготовке ко всем этапам всероссийской олимпиады школьников по математике необходимо
пользоваться следующими источниками:
Журналы:
«Квант», «Квантик», «Математика в школе», «Математика для школьников»
Книги и методические пособия:
Агаханов Н.Х., Подлипский О.К. Математика. Районные олимпиады. 6-11 класс. – М.:Просвещение, 2010.
Агаханов Н.Х., Богданов И.И., Кожевников П.А., Подлипский О.К., Терешин Д.А. Математика. Всероссийские олимпиады. Выпуск 1. – М.: Просвещение, 2008.
Журналы:
«Квант», «Квантик», «Математика в школе», «Математика для школьников»
Книги и методические пособия:
Агаханов Н.Х., Подлипский О.К. Математика. Районные олимпиады. 6-11 класс. – М.:Просвещение, 2010.
Агаханов Н.Х., Богданов И.И., Кожевников П.А., Подлипский О.К., Терешин Д.А. Математика. Всероссийские олимпиады. Выпуск 1. – М.: Просвещение, 2008.
Слайд 37Агаханов Н.Х., Подлипский О.К. Математика. Всероссийские олимпиады. Выпуск 2. – М.:
Просвещение, 2009.
Агаханов Н.Х., Подлипский О.К., Рубанов И.С. Математика. Всероссийские олимпиады. Выпуск 3. – М.: Просвещение, 2011
Агаханов Н.Х., Подлипский О.К., Рубанов И.С. Математика. Всероссийские олимпиады. Выпуск 4. – М.: Просвещение, 2013.
Адельшин А.В.,Кукина Е.Г.,Латыпов И.А. и др. Математическая олимпиада им. Г. П. Кукина. Омск, 2007-2009. – М.: МЦНМО, 2011.
Агаханов Н.Х., Подлипский О.К., Рубанов И.С. Математика. Всероссийские олимпиады. Выпуск 3. – М.: Просвещение, 2011
Агаханов Н.Х., Подлипский О.К., Рубанов И.С. Математика. Всероссийские олимпиады. Выпуск 4. – М.: Просвещение, 2013.
Адельшин А.В.,Кукина Е.Г.,Латыпов И.А. и др. Математическая олимпиада им. Г. П. Кукина. Омск, 2007-2009. – М.: МЦНМО, 2011.
Слайд 38Андреева А.Н. ,Барабанов А.И., Чернявский И.Я. Саратовские математические олимпиады.1950/51–1994/95. (2-e. исправленное
и дополненное). – М.: МЦНМО, 2013.
Бабинская И.Л. Задачи математических олимпиад. М.: Наука, 1975.
Блинков А.Д., Горская Е.С., Гуровиц В.М. (сост.). Московские математические регаты. Часть 1. 1998– 2006 – М.: МЦНМО, 2014.
Блинков А.Д. (сост.). Московские математические регаты. Часть 2. 2006– 2013 – М.: МЦНМО, 2014.
Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математические кружки. – Киров: Аса, 1994.
Горбачев Н.В. Сборник олимпиадных задач по математике (3-е изд., стереотип.). – М.: МЦНМО, 2013.
Бабинская И.Л. Задачи математических олимпиад. М.: Наука, 1975.
Блинков А.Д., Горская Е.С., Гуровиц В.М. (сост.). Московские математические регаты. Часть 1. 1998– 2006 – М.: МЦНМО, 2014.
Блинков А.Д. (сост.). Московские математические регаты. Часть 2. 2006– 2013 – М.: МЦНМО, 2014.
Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математические кружки. – Киров: Аса, 1994.
Горбачев Н.В. Сборник олимпиадных задач по математике (3-е изд., стереотип.). – М.: МЦНМО, 2013.
Слайд 39Гордин Р.К. Это должен знать каждый матшкольник (6-е издание, стереотипное). —
М., МЦНМО, 2011.
Гордин Р.К. Это должен знать каждый матшкольник (6-е издание, стереотипное). — М., МЦНМО, 2011
Гордин Р.К. Геометрия. Планиметрия. 7–9 классы (5-е издание, стереотипное). — М., МЦНМО, 2012.
Канель-Белов А.Я., Ковальджи А.К. Как решают нестандартные задачи (8-е, стереотипное). — М., МЦНМО, 2014.
Кноп К.А. Взвешивания и алгоритмы: от головоломок к задачам (3-е, стереотипное). — М., МЦНМО, 2014
Козлова Е. Г.. Сказки и подсказки (задачи для математического кружка) (7-е издание, стереотипное).— М., МЦНМО, 2013.
Гордин Р.К. Это должен знать каждый матшкольник (6-е издание, стереотипное). — М., МЦНМО, 2011
Гордин Р.К. Геометрия. Планиметрия. 7–9 классы (5-е издание, стереотипное). — М., МЦНМО, 2012.
Канель-Белов А.Я., Ковальджи А.К. Как решают нестандартные задачи (8-е, стереотипное). — М., МЦНМО, 2014.
Кноп К.А. Взвешивания и алгоритмы: от головоломок к задачам (3-е, стереотипное). — М., МЦНМО, 2014
Козлова Е. Г.. Сказки и подсказки (задачи для математического кружка) (7-е издание, стереотипное).— М., МЦНМО, 2013.
Слайд 40Кордемский Б.А. Математическая смекалка. – М., ГИФМЛ, 1958 — 576 с.
Раскина И.
В, Шноль Д. Э. Логические задачи. – М.: МЦНМО, 2014.
Интернет-ресурс: http://www.problems.ru/
Интернет-ресурс: http://www.problems.ru/