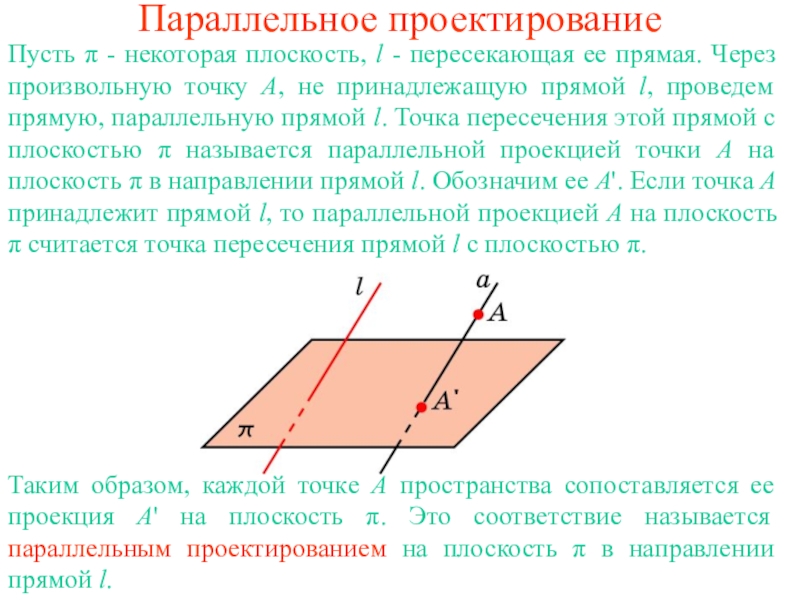
Пусть π - некоторая плоскость, l - пересекающая ее прямая. Через произвольную точку A, не принадлежащую прямой l, проведем прямую, параллельную прямой l. Точка пересечения этой прямой с плоскостью π называется параллельной проекцией точки A на плоскость π в направлении прямой l. Обозначим ее A'. Если точка A принадлежит прямой l, то параллельной проекцией A на плоскость π считается точка пересечения прямой l с плоскостью π.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Наглядный материал по математике на тему Параллельное проектирование
Содержание
- 1. Наглядный материал по математике на тему Параллельное проектирование
- 2. Свойство 1Если прямая параллельна или совпадает с
- 3. Свойство 2 Параллельное проектирование сохраняет отношение длин отрезков,
- 4. Свойство 3Если две параллельные прямые не параллельны
- 5. Упражнение 1В каком случае параллельной проекцией прямой будет точка? Ответ: Если прямая параллельна направлению проектирования.
- 6. Упражнение 2Сколько точек может получиться при параллельном
- 7. Упражнение 3Какие фигуры могут служить параллельными проекциями
- 8. Упражнение 4В каком случае параллельной проекцией двух
- 9. Упражнение 5В каком случае параллельной проекцией двух
- 10. Упражнение 6Какие фигуры могут быть параллельными проекциями
- 11. Упражнение 7Как должны быть расположены прямая и
- 12. Упражнение 8Как должны быть расположены две прямые,
- 13. Упражнение 9Как должны быть расположены две прямые,
- 14. Упражнение 10Сохраняются ли при параллельном проектировании величины углов?Ответ: Нет.
- 15. Упражнение 11Сохраняются ли при параллельном проектировании длины отрезков?Ответ: Нет.
- 16. Упражнение 12Может ли параллельная проекция угла быть больше (меньше) самого угла?Ответ: Да.
- 17. Упражнение 13Может ли параллельная проекция отрезка быть больше (меньше) самого отрезка?Ответ: Да.
- 18. Упражнение 14Верно ли, что если длина отрезка
- 19. Упражнение 15Точки A’, B’ являются параллельными проекциями
Свойство 1Если прямая параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.
Слайд 1Параллельное проектирование
Таким образом, каждой точке A пространства сопоставляется ее проекция A'
на плоскость π. Это соответствие называется параллельным проектированием на плоскость π в направлении прямой l.
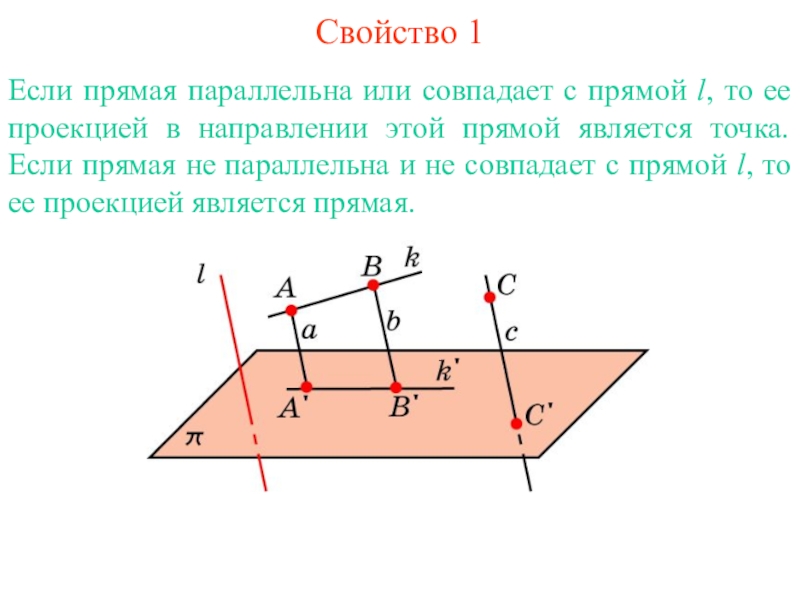
Слайд 2Свойство 1
Если прямая параллельна или совпадает с прямой l, то ее
проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.
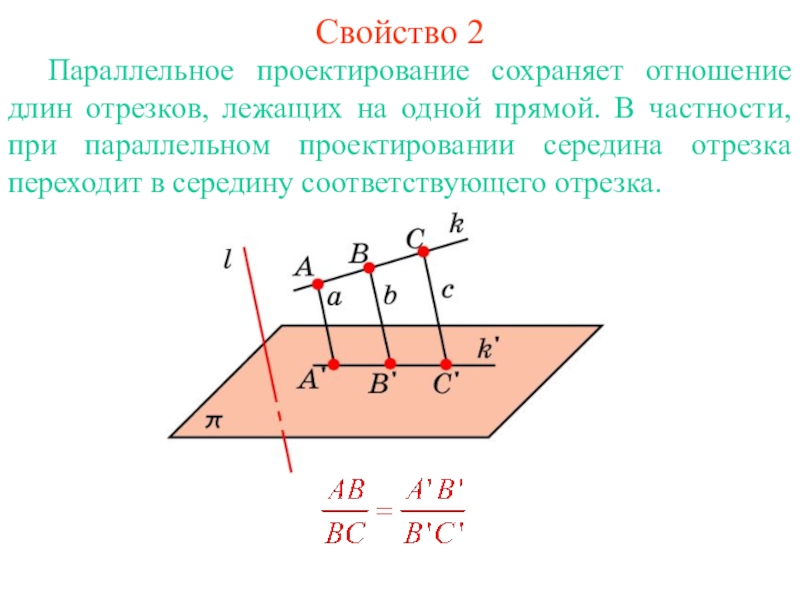
Слайд 3Свойство 2
Параллельное проектирование сохраняет отношение длин отрезков, лежащих на одной прямой.
В частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка.
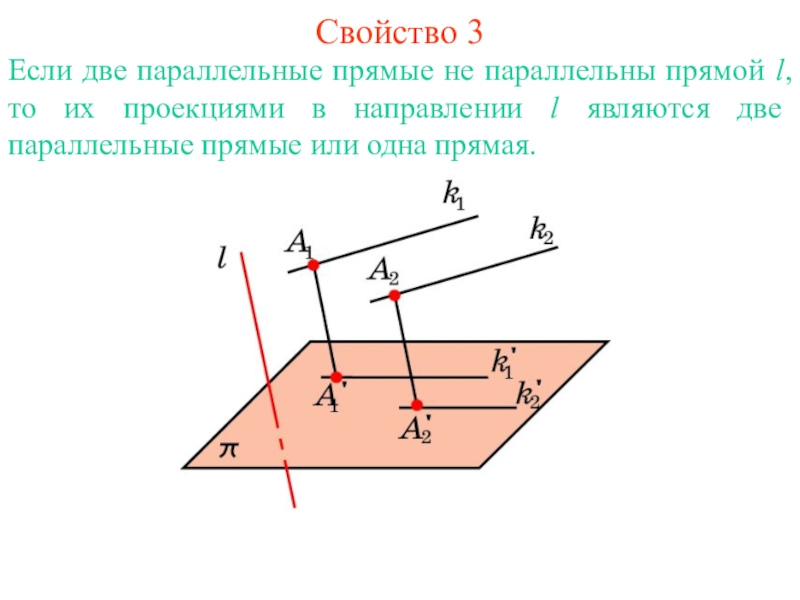
Слайд 4Свойство 3
Если две параллельные прямые не параллельны прямой l, то их
проекциями в направлении l являются две параллельные прямые или одна прямая.
Слайд 5Упражнение 1
В каком случае параллельной проекцией прямой будет точка?
Ответ: Если
прямая параллельна направлению проектирования.
Слайд 6Упражнение 2
Сколько точек может получиться при параллельном проектировании трех различных точек
пространства?
Ответ: Три, или две, или одна.
Слайд 7Упражнение 3
Какие фигуры могут служить параллельными проекциями двух пересекающихся прямых?
Ответ:
Две пересекающиеся прямые или одна прямая.
Слайд 8Упражнение 4
В каком случае параллельной проекцией двух параллельных прямых является одна
прямая?
Ответ: Если они лежат в плоскости, параллельной направлению проектирования, но не параллельны ему.
Слайд 9Упражнение 5
В каком случае параллельной проекцией двух параллельных прямых являются две
точки?
Ответ: Если они параллельны направлению проектирования.
Слайд 10Упражнение 6
Какие фигуры могут быть параллельными проекциями двух скрещивающихся прямых?
Ответ:
Пересекающиеся прямые, параллельные прямые, прямая и точка.
Слайд 11Упражнение 7
Как должны быть расположены прямая и точка, чтобы они проектировались
на плоскость в прямую и точку, принадлежащую этой прямой?
Ответ: Прямая не параллельна направлению проектирования, и через эту прямую и данную точку проходит плоскость, параллельная направлению проектирования.
Слайд 12Упражнение 8
Как должны быть расположены две прямые, чтобы они проектировались на
плоскость в прямую и точку, принадлежащую этой прямой?
Ответ: Пересекаться и одна из них параллельна направлению проектирования.
Слайд 13Упражнение 9
Как должны быть расположены две прямые, чтобы они проектировались на
плоскость в прямую и точку, не принадлежащую этой прямой?
Ответ: Скрещиваться и одна из них параллельна направлению проектирования.
Слайд 16Упражнение 12
Может ли параллельная проекция угла быть больше (меньше) самого угла?
Ответ:
Да.
Слайд 17Упражнение 13
Может ли параллельная проекция отрезка быть больше (меньше) самого отрезка?
Ответ:
Да.
Слайд 18Упражнение 14
Верно ли, что если длина отрезка равна длине его параллельной
проекции, то отрезок параллелен плоскости проектирования?
Ответ: Нет.
Слайд 19Упражнение 15
Точки A’, B’ являются параллельными проекциями точек A, B. AA’
= a, BB’ = b. Точка C делит отрезок AB в отношении m : n. Найдите расстояние между точкой C и ее проекцией C’.
