- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Метод координат в пространстве
Содержание
- 1. Метод координат в пространстве
- 2. Цель : обобщение и систематизация знаний по теме « Метод координат в пространстве
- 3. Прямоугольная система координат в пространствеЕсли через точку
- 4. x
- 5. В Е К Т О Р - это направленный отрезок Начало вектора Конец вектораа
- 6. КОЛЛИНЕАРНЫЕ ВЕКТОРЫ - это векторы, лежащие на одной или на параллельных прямыхаbc
- 7. СОНАПРАВЛЕННЫЕ ВЕКТОРЫ - это векторы, имеющие одно направлениеаb
- 8. Если векторы сонаправлены и их длины равны, то эти векторы называются РАВНЫМИаb
- 9. СЛОЖЕНИЕ ВЕКТОРОВДля любых векторов справедливы равенства:a+b=b+a (переместительный закон)(a+b)+c=a+ (b+c) (сочетательный закон) aba+b
- 10. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО(kl) a =k (la)
- 11. Угол между прямыми
- 12. Координаты правильной треугольной призмы
- 13. Координаты правильной шестиугольной призмы
- 14. Координаты правильной четырехугольной пирамиды
- 15. Слайд 15
- 16. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- 17. Уравнение плоскостиЕсли плоскость проходит через начало координат,
- 18. Расстояние между параллельными плоскостями
- 19. Угол между плоскостями
- 20. Определение луча на координатной плоскости.Точка О разделяет
- 21. Прямоугольная система координатВ прямоугольной системе координат каждой
- 22. Нахождение точки на координатной плоскости.Если, например, точка
- 23. Координаты вектораНа каждом из положительных полуосей отложим
- 24. Разложение по координатным векторамЛюбой вектор a можно
- 25. Запись координат вектора.Координаты вектора а будут записываться
- 26. Нулевой вектор и равные вектораТак как нулевой
- 27. Правила нахождения суммы, разности и произведения на
- 28. Правило №2Каждая координата разности двух векторов равна
- 29. Правило №3Каждая координата произведения вектора на число
- 30. Связь между координатами векторов и координатами точек.Вектор,
- 31. Простейшие задачи в координатахКаждая координата середины отрезка
- 32. Расстояние между точкамиРасстояния между точка M (x
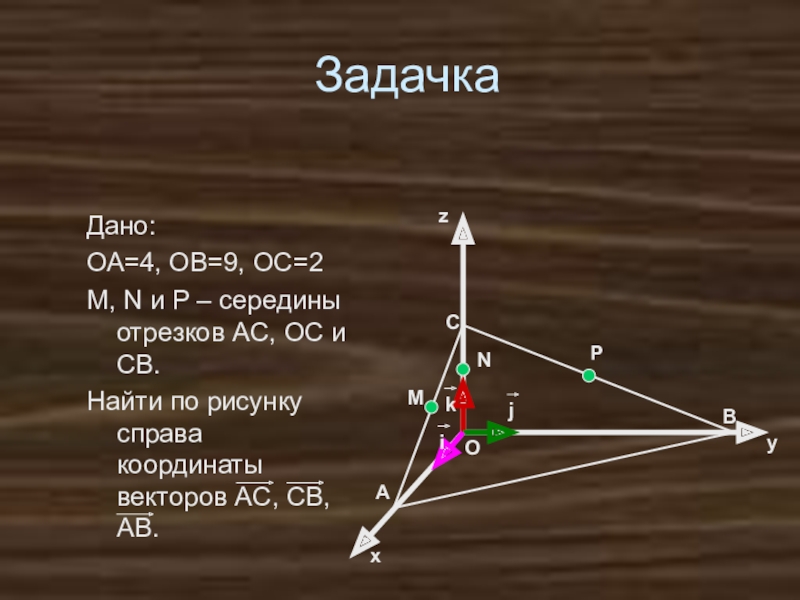
- 33. ЗадачкаДано: ОА=4, ОВ=9, ОС=2M, N и P
- 34. Решение:AC = AO + OC = 4i
- 35. Спасибо за внимание!!!Презентация сделана по учебнику геометрии
Слайд 1Метод координат в пространстве
Координаты точки и координаты вектора
Выполнили:
курсанты 111 группы
Ващенко Дмитрий
Галайчук
Слайд 3Прямоугольная система координат в пространстве
Если через точку пространства проведены три попарно
Рассмотрим рисунок
Слайд 4 x
y
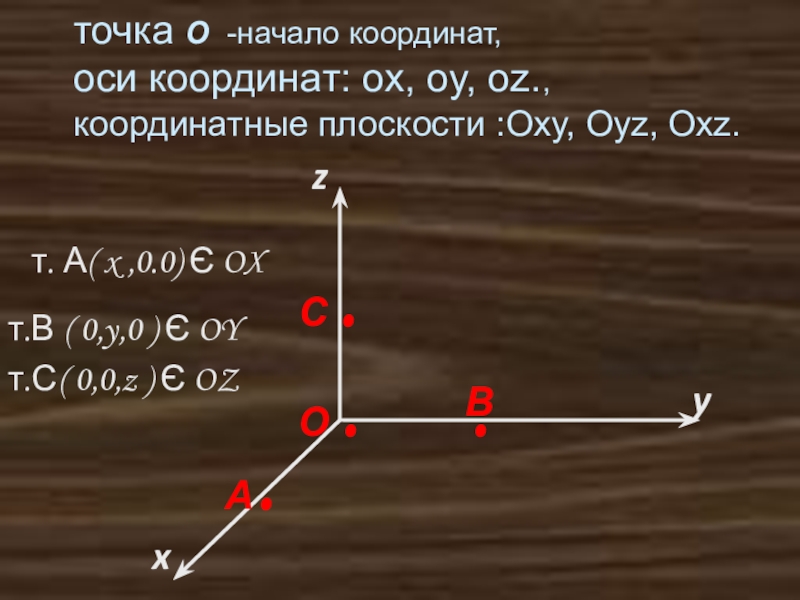
точка О -начало координат,
оси координат: ox, oy, oz.,
координатные плоскости :Оxy, Oyz, Oxz.
т. А( x ,0.0) Є OX
т.В ( 0,y,0 ) Є OY
т.С( 0,0,z ) Є OZ
О .
.
А.
В
С .
Слайд 9СЛОЖЕНИЕ ВЕКТОРОВ
Для любых векторов справедливы равенства:
a+b=b+a (переместительный закон)
(a+b)+c=a+ (b+c) (сочетательный закон)
a
b
a+b
Слайд 10УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
(kl) a =k (la) - сочетательный закон
k
(k + l) a = ka + la - 2-ой распределительный закон
Слайд 17Уравнение плоскости
Если плоскость проходит через начало координат, то d=0
Если плоскость пересекает
уравнение плоскости в отрезках
Слайд 20Определение луча на координатной плоскости.
Точка О разделяет каждую из осей координат
Слайд 21Прямоугольная система координат
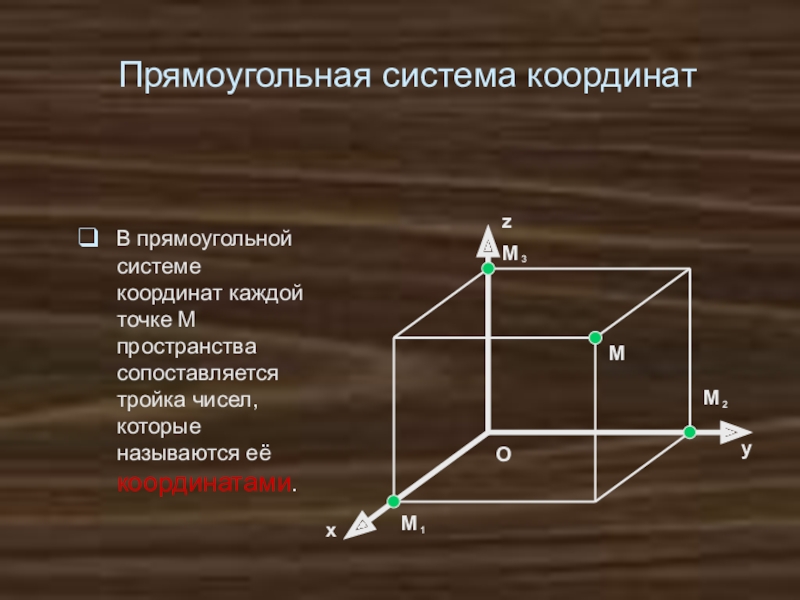
В прямоугольной системе координат каждой точке M пространства сопоставляется
y
z
x
M
1
M
2
M
3
M
O
Слайд 22Нахождение точки на координатной плоскости.
Если, например, точка M лежит на координатной
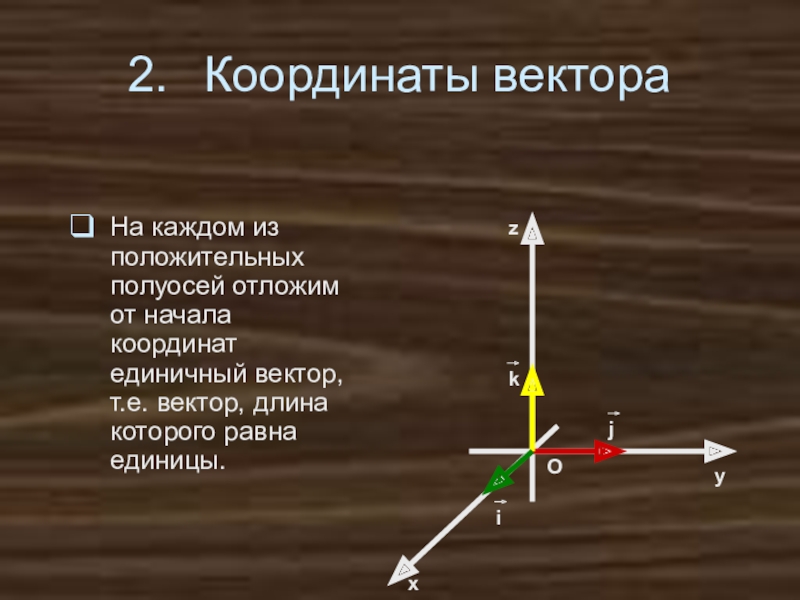
Слайд 23Координаты вектора
На каждом из положительных полуосей отложим от начала координат единичный
j
k
i
y
z
x
O
Слайд 24Разложение по координатным векторам
Любой вектор a можно разложить по координатным векторам,
а = xi + yj + zk
Причем коэффициенты разложения x, y, z определяются единственным образом.
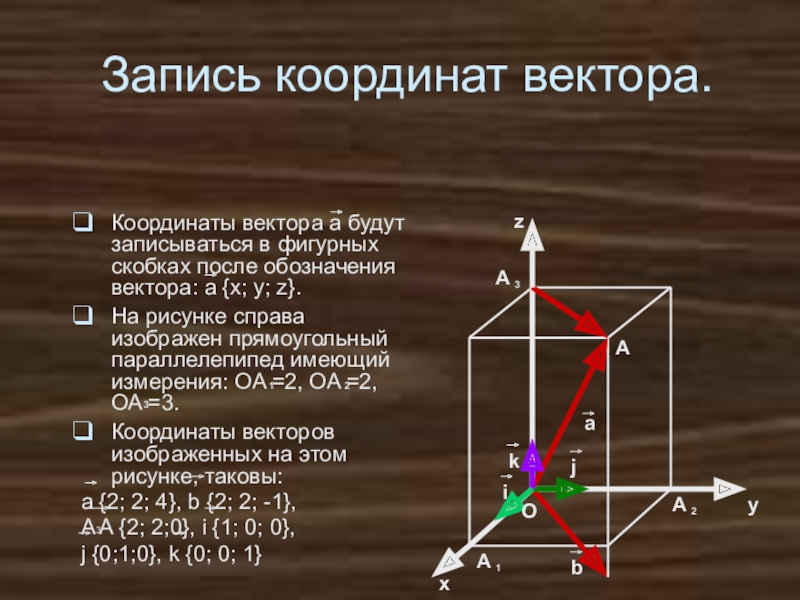
Слайд 25Запись координат вектора.
Координаты вектора а будут записываться в фигурных скобках после
На рисунке справа изображен прямоугольный параллелепипед имеющий измерения: OA =2, OA =2, OA =3.
Координаты векторов изображенных на этом рисунке, таковы:
a {2; 2; 4}, b {2; 2; -1},
A A {2; 2;0}, i {1; 0; 0},
j {0;1;0}, k {0; 0; 1}
A
A
A
A
O
y
x
z
a
j
i
k
b
3
2
1
1
2
3
3
Слайд 26Нулевой вектор и равные вектора
Так как нулевой вектор можно представить в
Координаты равных векторов соответственно равны, т.е. если векторы
a {x ; y ; z } и b {x ; y ; z } равны, то x =x , y =y и z =z .
1
1
1
2
Слайд 27Правила нахождения суммы, разности и произведения на данное число.
Каждая координата суммы
{x +x ; y +y ; z +z }
1
2
1
2
1
2
2
2
2
1
1
1
Слайд 28Правило №2
Каждая координата разности двух векторов равна разности соответствующих координат этих
{x –x ; y –y ; z –z }
1
2
1
2
1
2
1
2
1
1
2
2
Слайд 29Правило №3
Каждая координата произведения вектора на число равна произведение соответствующей координаты
{ x; y; z}
α
α
α
Слайд 30Связь между координатами векторов и координатами точек.
Вектор, конец которого совпадает с
Координаты любой точки равны соответствующим координатам её радиус-вектора.
Каждая координата вектора равна разности соответствующих координат его конца и начала.
Слайд 31Простейшие задачи в координатах
Каждая координата середины отрезка равна полусумме соответствующих координат
Длина вектора a {x; y; z} вычисляется по формуле
|a| = √x² + y² + z²
Слайд 32Расстояние между точками
Расстояния между точка M (x ; y ; z
M (x ; y ; z ) вычисляется по формуле
d = √(x – x )² + (y – y )² + (z – z )²
Слайд 33Задачка
Дано:
ОА=4, ОВ=9, ОС=2
M, N и P – середины отрезков AC,
Найти по рисунку справа координаты векторов AC, CB, AB.
P
B
y
N
j
i
k
M
O
C
A
x
z
Слайд 34Решение:
AC = AO + OC = 4i + 2k, AC {-4;
CB = CO + OB = 2k + 9j, CB {0; 9; 2}
AB = AO + OB = -4i + 9j, AB {-4; 7; 0}