- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Математические софизмы
Содержание
- 1. Математические софизмы
- 2. Исаак Ньютон«В математических вопросах нельзя пренебрегать даже
- 3. Результаты анкетирования
- 4. Что такое софизмы? Кто их выдумал? Имеют
- 5. Задачи:Узнать о истории возникновения софизмов Узнать основные
- 6. Понятие софизмаТермин «софизм» происходит от греческого слова,
- 7. Немного из истории софизмаСофизмы появились еще в
- 8. Один из древних софизмов :
- 9. Математические софизмыАрифметическиеАлгебраическиеГеометрические
- 10. Арифметические софизмы «Два умножить на два
- 11. Алгебраические софизмы Всякое число равно своему удвоенному
- 12. Геометрические софизмыСофизм об исчезающем квадрате. Большой квадрат
- 13. Типичные ошибки в софизмах «Правильно понятая
- 14. Заключение Математические софизмы приучают
- 15. Николай Егорович Жуковский«Решайте задачи и не бойтесь
Слайд 1Математические софизмы
Автор:
студент 1 курса группы 14
Пежемский Р.Н
Руководитель:
преподаватель математики
Степанова
Слайд 2Исаак Ньютон
«В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками».
И. Ньютон.
Слайд 4Что такое софизмы?
Кто их выдумал?
Имеют ли они какое-нибудь логическое
Играют ли они какую-нибудь роль при изучении математики?
Цель моего исследования – познакомиться с математическими софизмами и выявить их значимость при изучении математики.
Слайд 5Задачи:
Узнать о истории возникновения софизмов
Узнать основные виды математических софизмов
Выделить
Объект исследования: математические софизмы.
Предмет исследования: значимость софизмов при изучении математики.
Методы исследования: изучение источников: литературы, энциклопедий, сайтов в Интернете, сравнение, обобщение, анкетирование студентов.
Гипотеза: разбор софизмов помогает сознательному усвоению изучаемого математического материала, развивает наблюдательность, вдумчивость и критическое отношение к тому, что изучается на занятиях.
Слайд 6Понятие софизма
Термин «софизм» происходит от греческого слова, означающего «измышление», «хитрость».
философ
Термин “софизм” впервые ввел Аристотель, охарактеризовавший софистику как мнимую, а не действительную мудрость.
Слайд 7Немного из истории софизма
Софизмы появились еще в Древней Греции.
Они тесно
Слайд 8Один из древних софизмов :
«Что ты не терял, то
Рога ты не терял.
Значит, у тебя рога».
Слайд 10Арифметические софизмы
«Два умножить на два будет пять: 2 ·
Имеем числовое равенство (верное): 4 : 4 = 5 : 5.
Вынесем за скобки в каждой части его общий множитель.
Получим: 4 · (1 : 1) = 5 · (1 : 1).
Числа в скобках равны, поэтому 4 = 5, или 2 · 2 = 5.
Вопрос: Где здесь ошибка?
Ответ: Ошибка допущена в вынесении общего множителя за скобки в левой и правой частях тождества
4 : 4 = 5 : 5
Слайд 11Алгебраические софизмы
Всякое число равно своему удвоенному значению.
Запишем очевидное для любого числа
а2 - а2 = а2 - а2.
Вынесем а в левой части за скобку, а правую часть разложим на множители по формуле разности квадратов, получив
а(а - а) = (а + а)(а - а). Разделив обе части на а - а, получим а = а + а, или
а =2а
Итак, всякое число равно своему удвоенному значению
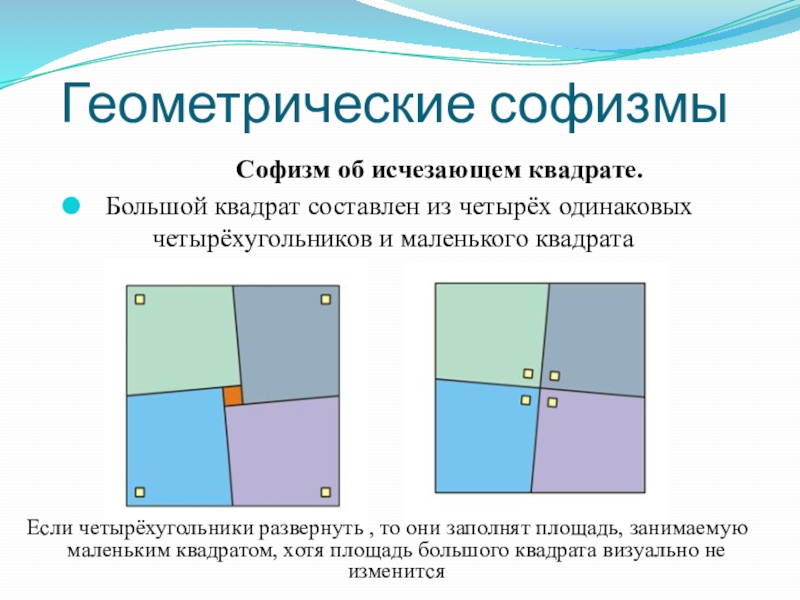
Слайд 12Геометрические софизмы
Софизм об исчезающем квадрате.
Большой квадрат составлен из четырёх одинаковых
Если четырёхугольники развернуть , то они заполнят площадь, занимаемую маленьким квадратом, хотя площадь большого квадрата визуально не изменится
Слайд 13Типичные ошибки в софизмах
«Правильно понятая ошибка — это путь к открытию»
деление на 0;
неправильные выводы из равенства произведений или дробей;
неправильное извлечение квадратного корня из квадрата выражения;
нарушения правил действия с именованными величинами;
неправильное вынесение общего множителя за скобки;
неравносильный переход от одного равенства или неравенства к другому.