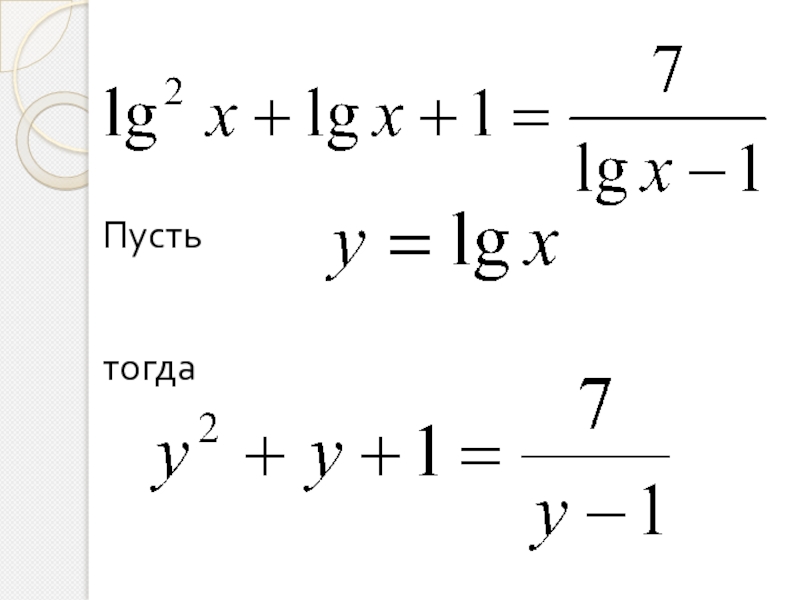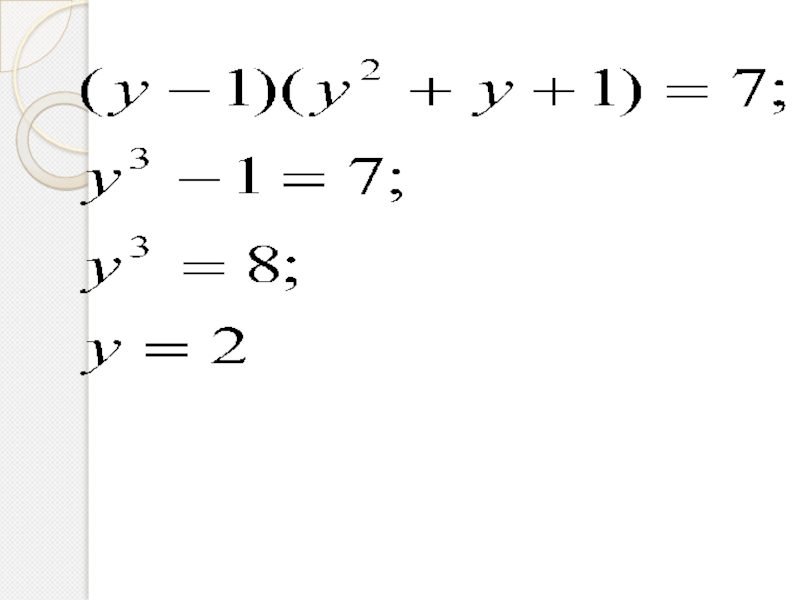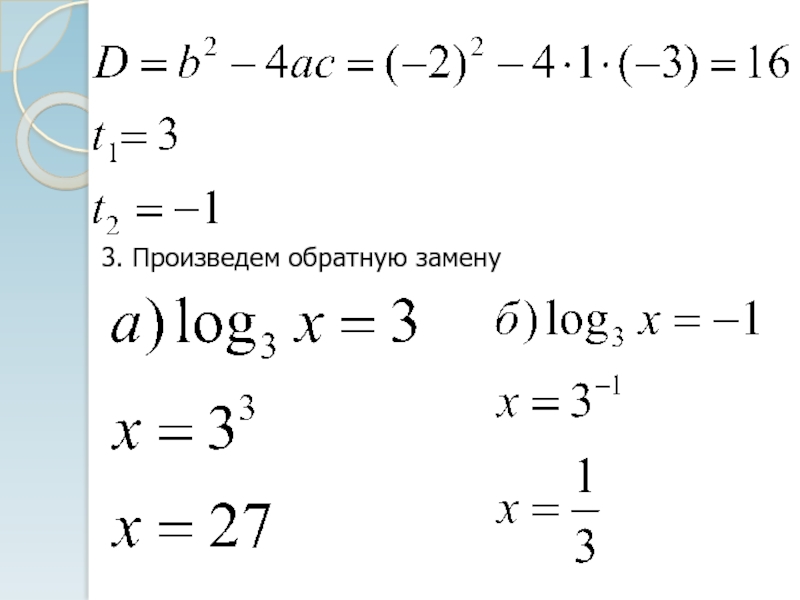- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Логарифмические уравнения
Содержание
- 1. Логарифмические уравнения
- 2. Ум заключается не только в знании, Но и умении прилагать знание в деле.Аристотель
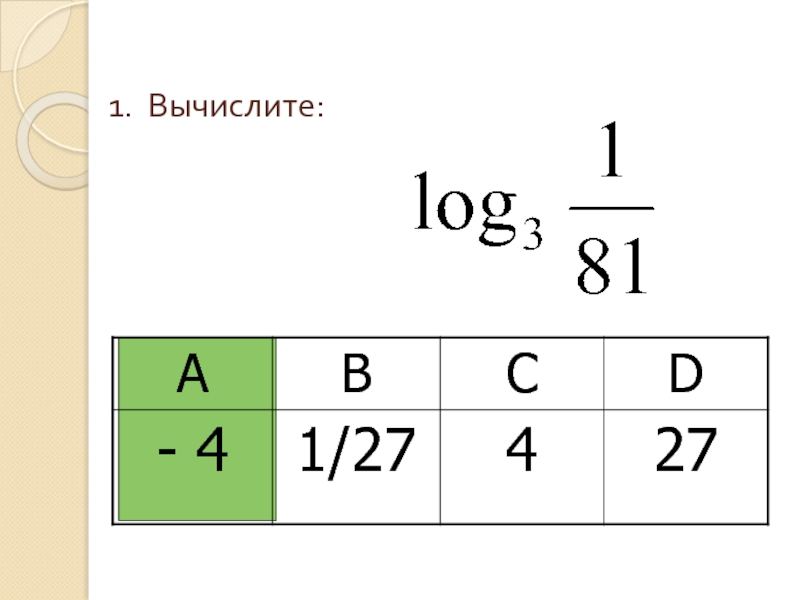
- 3. 1. Вычислите:
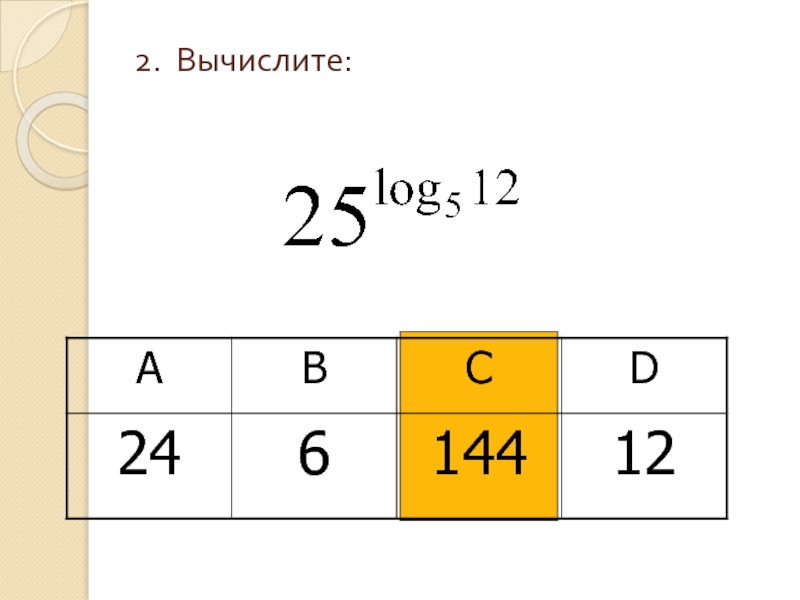
- 4. 2. Вычислите:
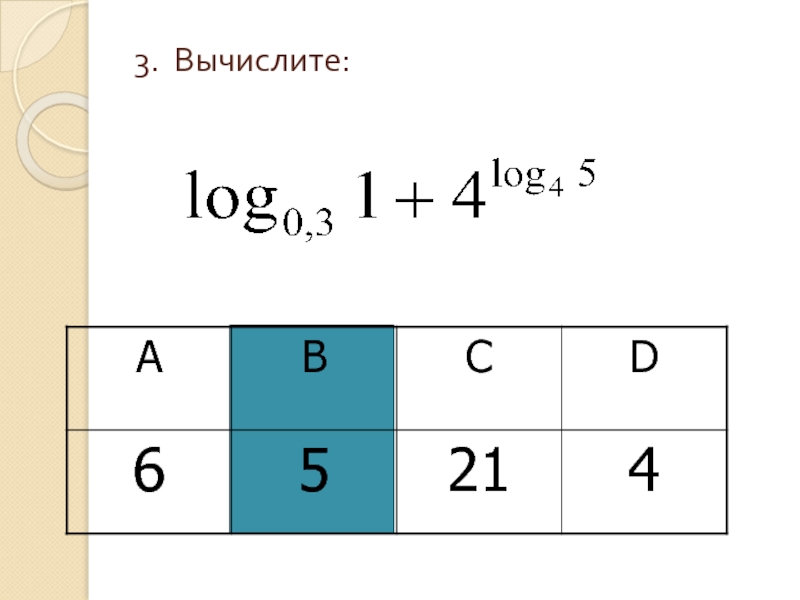
- 5. 3. Вычислите:
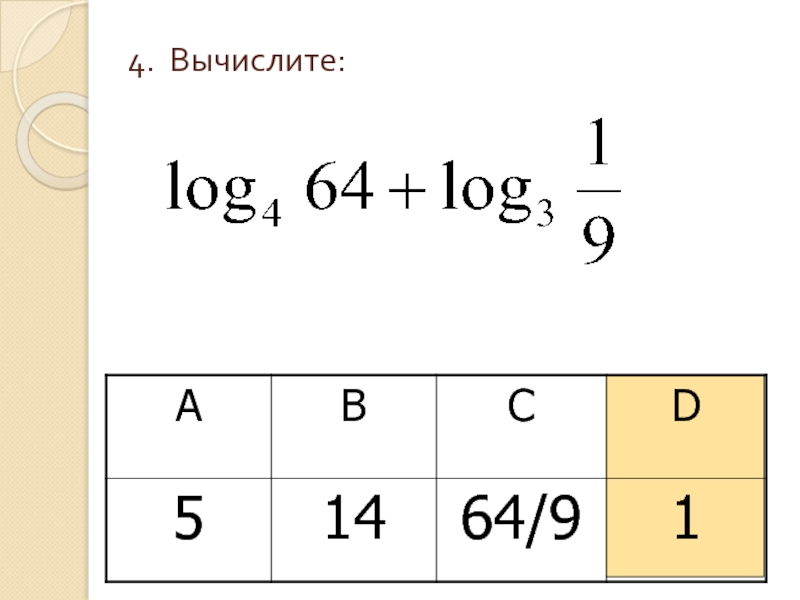
- 6. 4. Вычислите:
- 7. 5. Вычислите:
- 8. 6. Вычислите:
- 9. 7. Вычислите:
- 10. 8. Логарифм какого числа по основанию 2 равен 4:
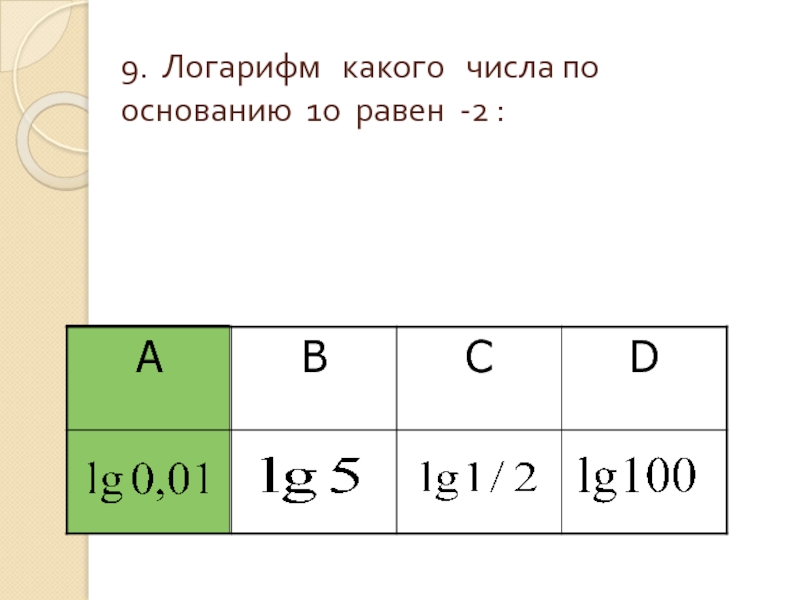
- 11. 9. Логарифм какого числа по основанию 10 равен -2 :
- 12. 10. Упростите:
- 13. 11. При каких значениях х выражение имеет смысл:
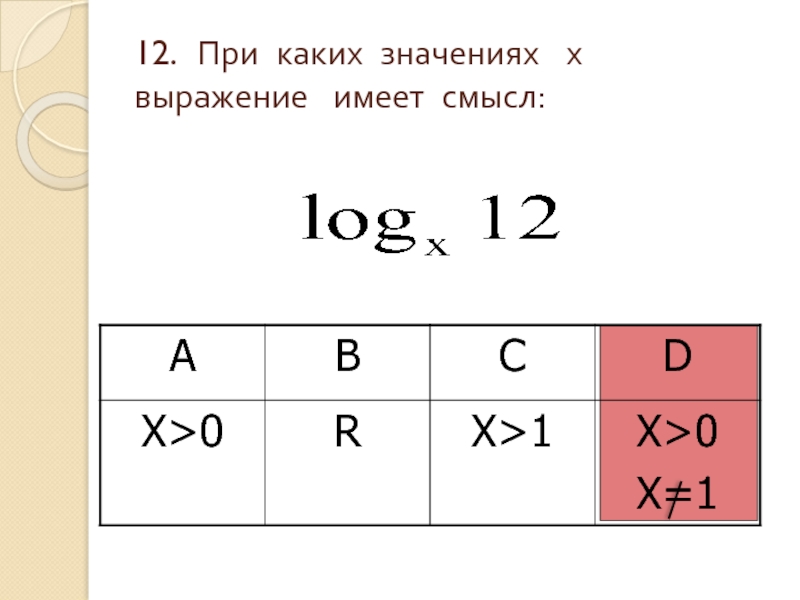
- 14. 12. При каких значениях х выражение имеет смысл:
- 15. 13. При каких значениях х выражение имеет смысл:
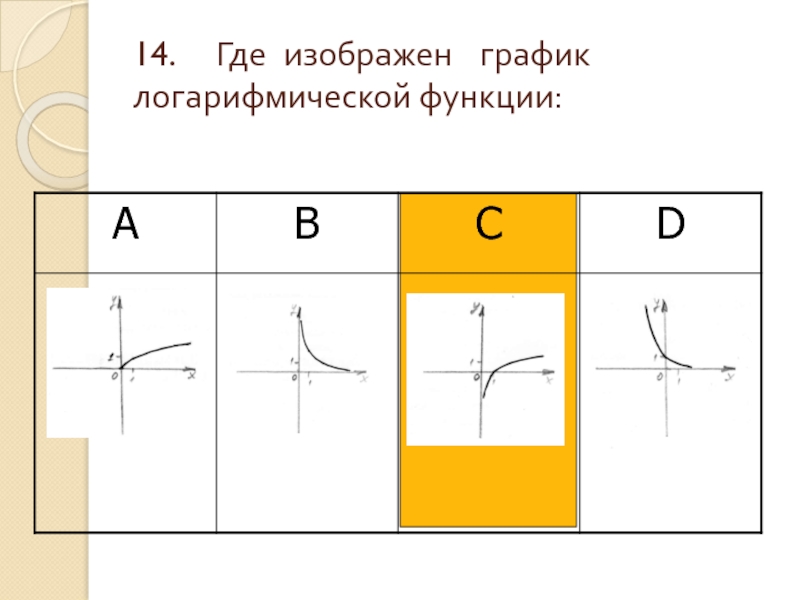
- 16. 14. Где изображен график логарифмической функции:
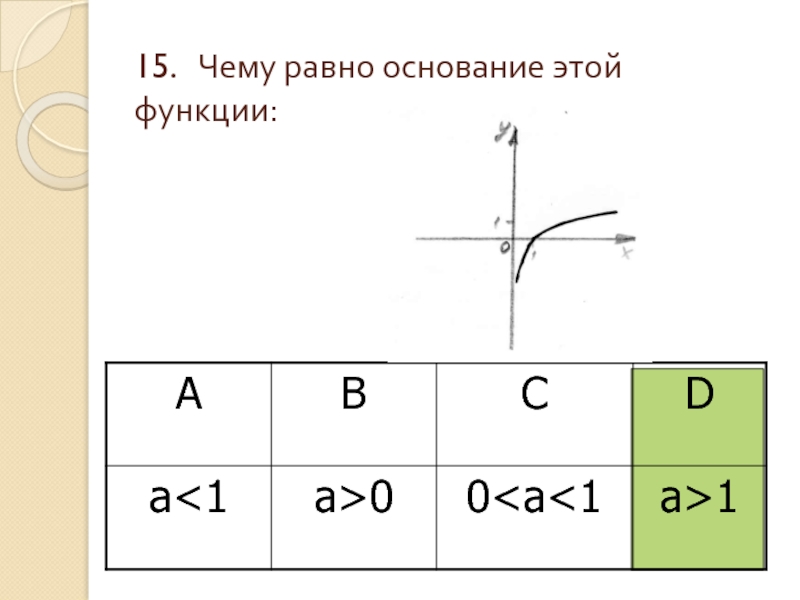
- 17. 15. Чему равно основание этой функции:
- 18. *К л а с с н а
- 19. Цель урока:Познакомиться с различными способами
- 20. Способы решения:По определению логарифма;Уравнивание логарифмов с
- 21. Определение : Уравнение, в котором неизвестное содержится под знаком логарифма или в его основании, называется логарифмическим.
- 22. Логарифм λογοζ(«логос» - отношение) и αριμοζ(«арифмос» - число)Джон Непер(1550-1617)
- 23. Решить уравнение.По определению логарифмаПо определению логарифма.Ответ: 243
- 24. 1. Решить уравнение:ООУ: т.к. Д(
- 25. 3.Основанные на свойствах логарифмов.
- 26. 2. По свойствам логарифма
- 27. 3. С учетом ООУ: 1- корень -5 – посторонний кореньОтвет: 1.
- 28. 4.Замена неизвестныхпо свойствам логарифма
- 29. Пустьтогда
- 30. Слайд 30
- 31. 3. Произведем обратную замену4. С учетом ООУ: 100- корень
- 32. 2. ПустьТогда уравнение примет вид 5. Сведение к квадратному.
- 33. 3. Произведем обратную замену
- 34. 4. С учетом ООУ: - корень27- корень Ответ: ,27.
- 35. 6.Разложение на множители.
- 36. Произведение равно нулю, если один из множителей равен нулю, а второй при этом не теряет смысла.
- 37. 4. С учетом ООУ: 1 - корень16 - корень Ответ: 1, 16.
- 38. В классе: № 337(1;3) № 338(1;3) Дома:П.19 № 337(2;4) № 338(2;4)
Ум заключается не только в знании, Но и умении прилагать знание в деле.Аристотель
Слайд 19Цель урока:
Познакомиться с различными способами решения логарифмических
уравнений;
Отработать алгоритм решения логарифмических уравнений.
Отработать алгоритм решения логарифмических уравнений.
Слайд 20 Способы решения:
По определению логарифма;
Уравнивание логарифмов с равными основаниями;
Основанные на свойствах
логарифмов;
Замена неизвестных;
Сведение к квадратному;
Разложение на множители.
Замена неизвестных;
Сведение к квадратному;
Разложение на множители.
Слайд 21Определение :
Уравнение, в котором неизвестное содержится под знаком логарифма или
в его основании, называется логарифмическим.
Слайд 241. Решить уравнение:
ООУ: т.к. Д( )=
, то 3х-2>0
x>2/3
x>2/3
3х-2=7
Х=3
Ответ: 3 с учетом ООУ.
2. Уравнивание логарифмов с равными основаниями.
Слайд 36Произведение равно нулю, если один из множителей равен нулю, а второй
при этом не теряет смысла.