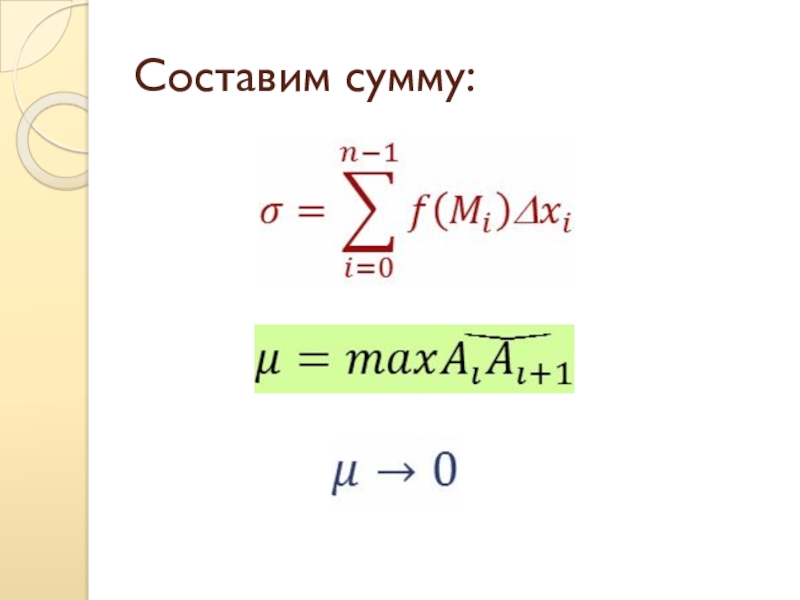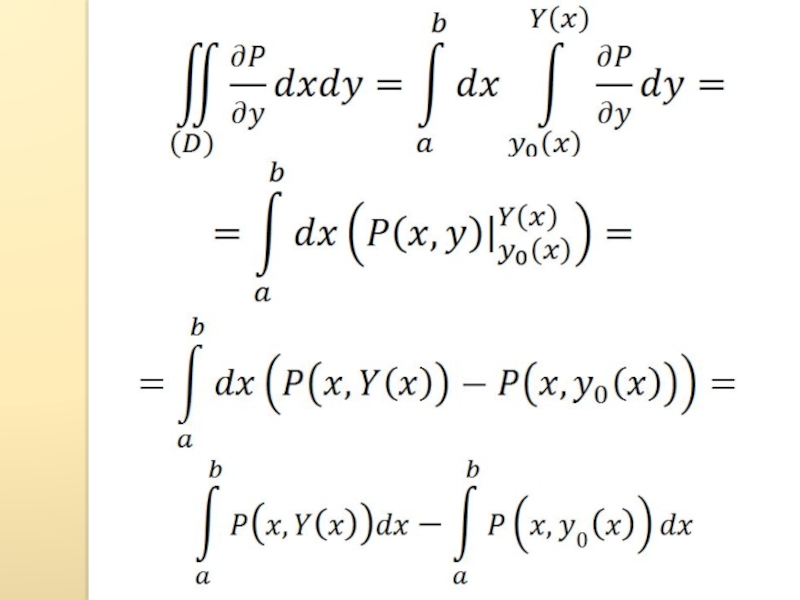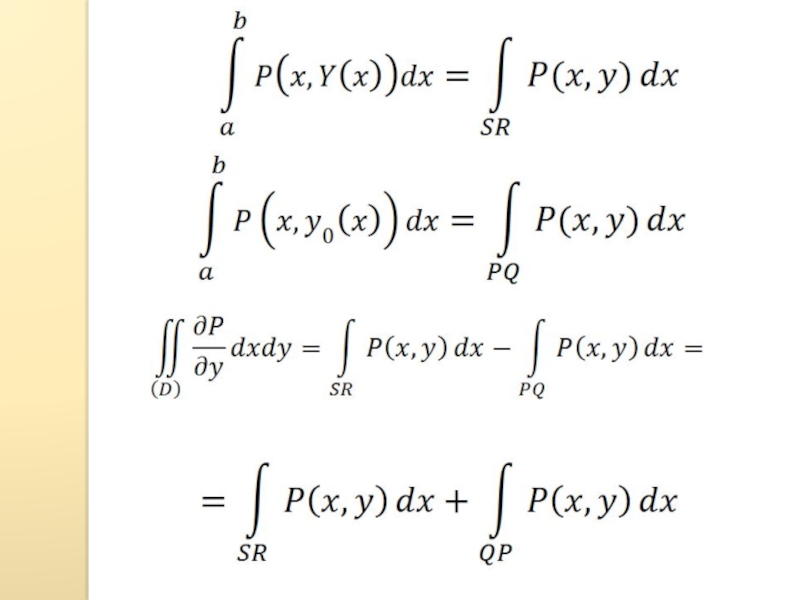группы
Айрапетова Виктория
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Криволинейные интегралы. Интегралы от полного дифференциала. Формула Грина
Содержание
- 1. Криволинейные интегралы. Интегралы от полного дифференциала. Формула Грина
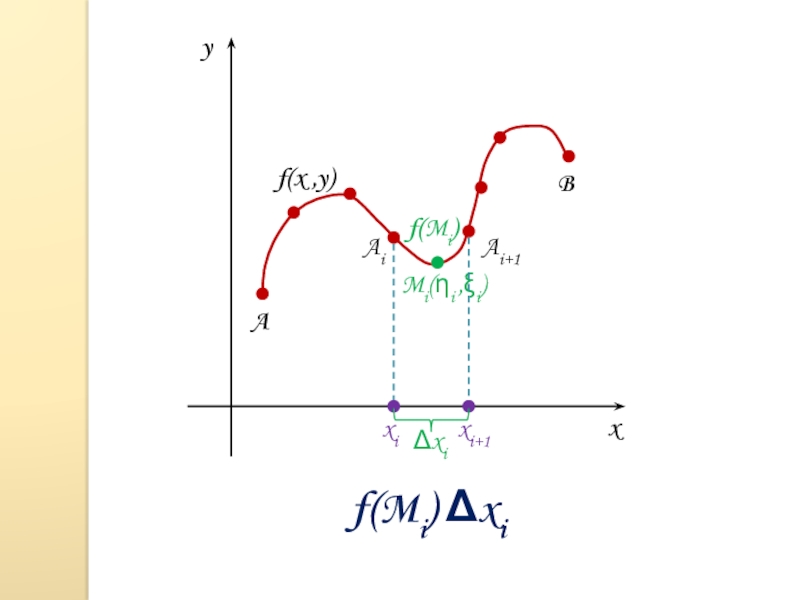
- 2. xyABf(x ,y)AiAi+1Mi(i ,i)f(Mi)xixi+1xi f(Mi) xi
- 3. Составим сумму:
- 4. Определение: Если при стремлении к нулю эта
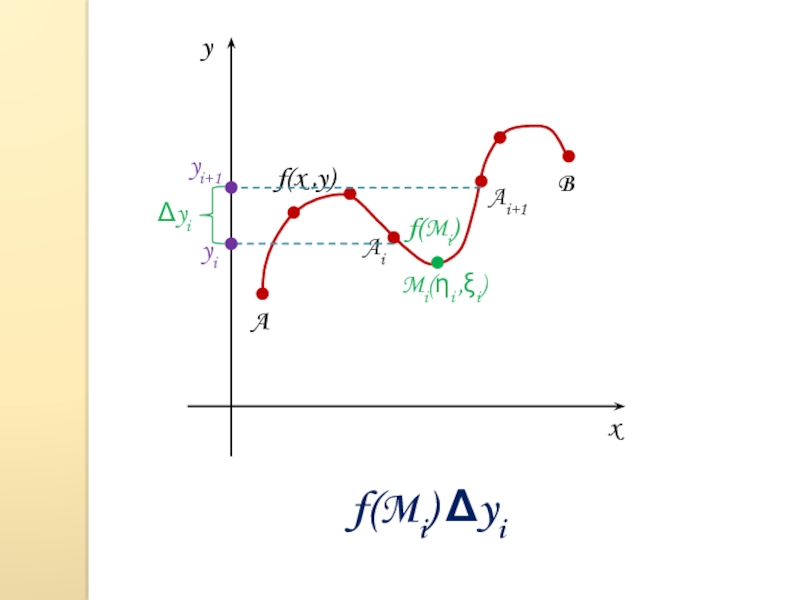
- 5. xyABf(x ,y)AiAi+1Mi(i ,i)f(Mi)yiyi+1yi f(Mi) yi
- 6. Составляя суммуПолучим криволинейный интеграл второго типа от :
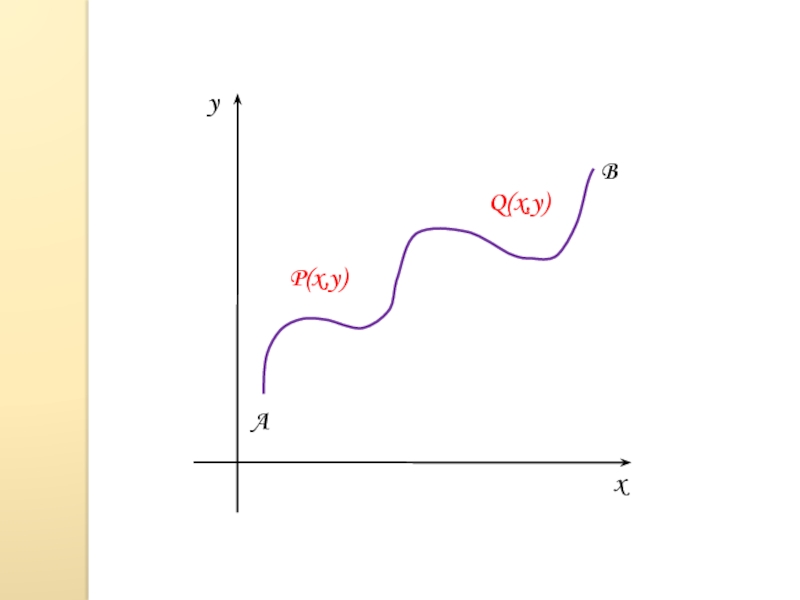
- 7. xyABP(x,y)Q(x,y)
- 8. Пусть существуют интегралы:их сумму называют криволинейным интегралом «общего вида»:
- 9. Кривая, заданная в трехмерном пространстве
- 10. Параметрически заданная криваяПустьФункции и непрерывны
- 11. Подобным же образом можно установить:
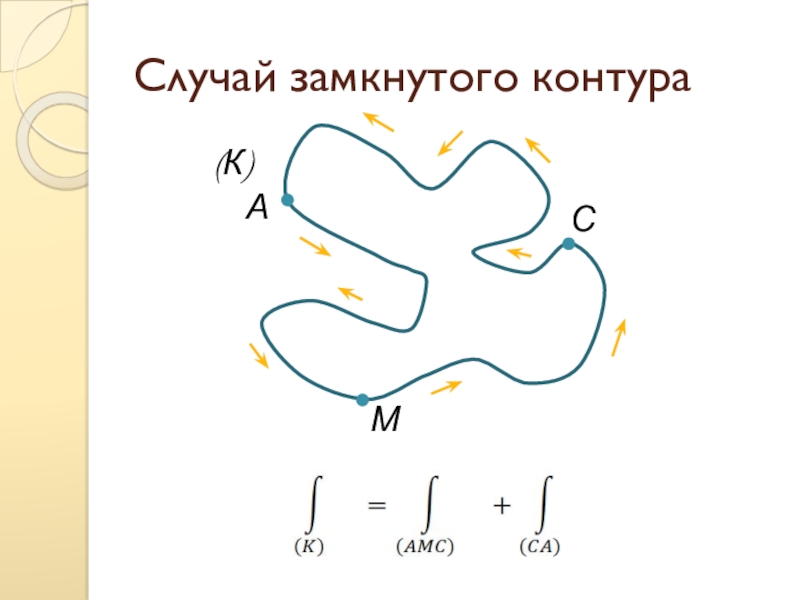
- 12. Случай замкнутого контура(К)АМС
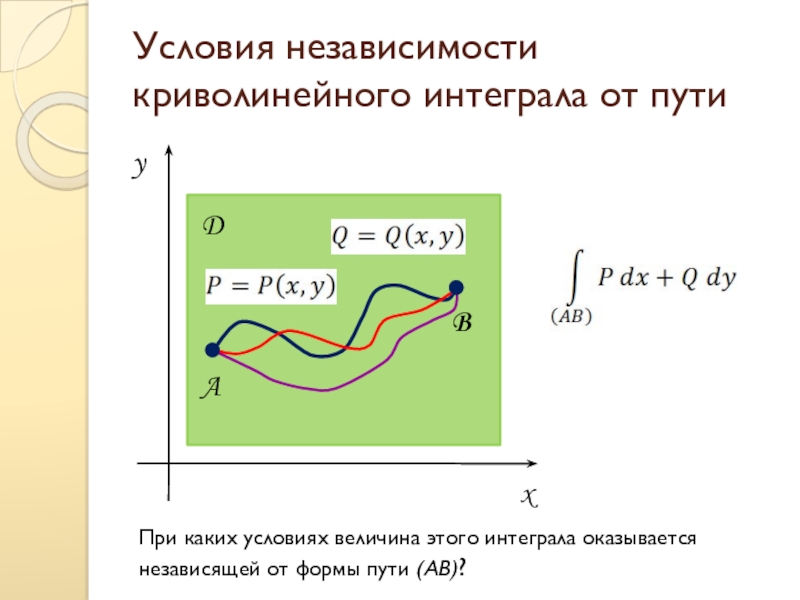
- 13. Условия независимости криволинейного интеграла от путиDABПри каких
- 14. Для того чтобы криволинейный интеграл не зависел
- 15. Тогда:
- 16. Для того чтобы криволинейный интеграл, где бы
- 17. Слайд 17
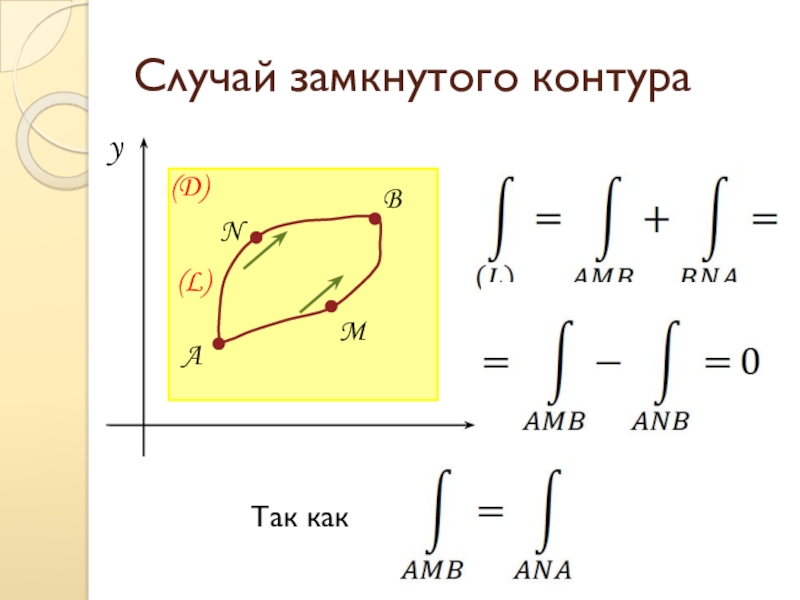
- 18. Случай замкнутого контураyx(D)ANBM(L)Так как
- 19. Рассмотрим область (D) – криволинейную трапецию:yxPSRQy=Y(x)y=y0(x)ab(D)SR: y=Y(x) a
- 20. В области (D) задана функция P(x,y) непрерывная
- 21. Слайд 21
- 22. Слайд 22
- 23. PSRQ(D)
- 24. Теперь рассмотрим:yxPSRQx=X(y)x=x0(y)cd(D)QR: x=X(y) c y dPS: x=x0(y) c y dSR, PQ|| OxO
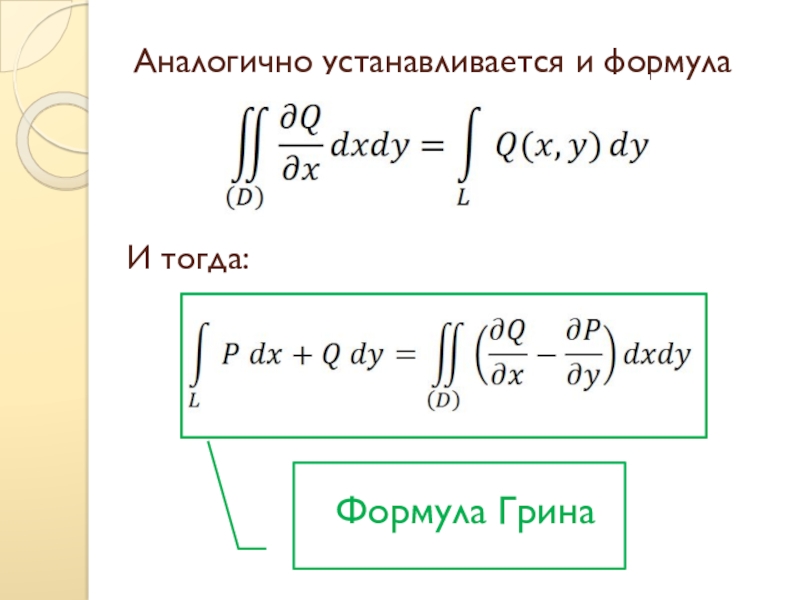
- 25. Аналогично устанавливается и формулаИ тогда:Формула Грина
xyABf(x ,y)AiAi+1Mi(i ,i)f(Mi)xixi+1xi f(Mi) xi
Слайд 1Криволинейные интегралы второго рода
Интегралы от полного дифференциала.
Формула Грина
Подготовила студентка 13.203(р)
Слайд 4Определение:
Если при стремлении к нулю эта сумма имеет конечный предел
I, то этот предел называется криволинейным интегралом второго рода от взятым по кривой (АВ) и обозначается:
Слайд 10Параметрически заданная кривая
Пусть
Функции и непрерывны и при изменении параметра
t от до кривая описывается в направлении от А к В. Функция f(x,y) непрерывна и существует и непрерывна производная ’(t). Тогда:
Слайд 13Условия независимости криволинейного интеграла от пути
D
A
B
При каких условиях величина этого интеграла
оказывается независящей от формы пути (АВ)?
y
x
Слайд 14Для того чтобы криволинейный интеграл не зависел от формы пути интегрирования,
необходимо и достаточно, чтобы дифференциальное выражение P dx + Q dy было в рассматриваемой области дифференциалом от некоторой функции двух переменных:
Слайд 16Для того чтобы криволинейный интеграл, где бы в области D ни
были взяты начальная и конечная точки А и В пути интегрирования, не зависел от формы этого пути, необходимо и достаточно:
Слайд 19Рассмотрим область (D) – криволинейную трапецию:
y
x
P
S
R
Q
y=Y(x)
y=y0(x)
a
b
(D)
SR: y=Y(x) a x b
PQ: y=y0(x) a
x b
PS, QR|| Oy
O
Слайд 20В области (D) задана функция P(x,y) непрерывная вместе со своей производной
Вычислим теперь двойной интеграл
Слайд 24Теперь рассмотрим:
y
x
P
S
R
Q
x=X(y)
x=x0(y)
c
d
(D)
QR: x=X(y) c y d
PS: x=x0(y) c y
d
SR, PQ|| Ox
O