- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Комбинаторные задачи (6 класс)
Содержание
- 1. Комбинаторные задачи (6 класс)
- 2. Комбинаторика – это область математики,
- 3. Готфрид Лейбниц Истоки этой науки были положены знаменитым немецким математиком и философом Готфридом Лейбницем.(1646-1716)
- 4. Правило умножения Пусть объект А выбирается n
- 5. №4921способ: составить дерево возможных вариантов2 способ:
- 6. ПредседательЗаместительСекретарькомиссияАПолученнаякомбинацияАБВАВББАВБВАВАБВБАБВБВАВАБВБВАБА1 способ
- 7. 2способ3213•2•1= 6
- 8. №493Сколько двузначных чисел можно составить из цифр
- 9. №4941)Сколько трехзначных чисел можно составить из
- 10. №495Несколько стран решили использовать для своего государственного
- 11. №496Несколько стран решили использовать для своего государственного
- 12. №497Руководство некоторой страны решило сделать свой государственный
- 13. №497.324··= 24
- 14. №498В списке учеников 6-го класса 15 девочек
- 15. №499а)В списке учеников 6 класса 15 девочек
- 16. №499б)В списке учеников 6 класса 15 девочек
- 17. №499вВ списке учеников 6 класса 15 девочек
- 18. №499 г)В списке учеников 6 класса 15
- 19. При решении этой задачи надо учесть, что
- 20. №500а,бВ списке учеников 6 класса 15 девочек
- 21. №500в)г)В списке учеников 6 класса 15 девочек
- 22. №501а) Сколько двузначных чисел можно составить из
- 23. №502а) Сколько трехзначных чисел можно составить
- 24. Ответ б) Ответ а)№503а)
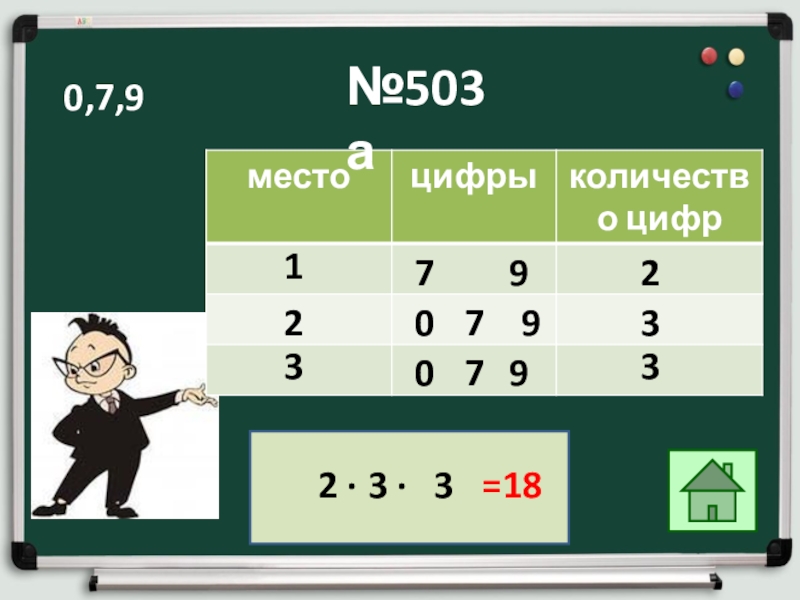
- 25. На первое место нельзя поставить цифру 0
- 26. №503а 17922 ∙2079330733 ∙3 =18 0,7,99
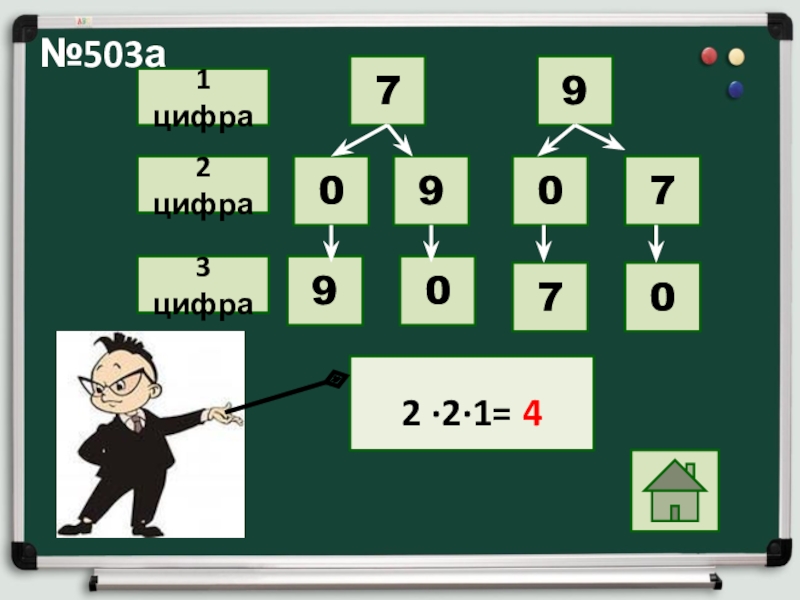
- 27. 70907990701 цифра2 цифра3 цифра2 ∙2∙1= 4 №503а
- 28. №506В 6 а классе в четверг 5
- 29. №508В чемпионате России по футболу в высшей
- 30. №509аВ двух урнах имеется по семь шаров,
- 31. №509бВ двух урнах имеется по семь шаров,
- 32. №509вВ двух урнах имеется по семь шаров,
- 33. Самостоятельная работа1. Сколько двузначных чисел можно составить
- 34. Самостоятельная работаВариант 1Вариант 22. Сколько трехзначных чисел
- 35. Самостоятельная работаВариант 1Вариант 23. В списке баскетбольной
- 36. Разберем решение задач:1. Сколько двузначных чисел можно
- 37. Решение2. Сколько трехзначных чисел можно составить из
- 38. РешениеВариант 1Вариант 23.В списке баскетбольной команды 20
- 39. Ответы123а)3∙3=9 б)3∙2=6а)3∙4∙4=48б)3∙3∙2 =18а)(12∙11∙10):6=48 б)(8∙7):2=28а)4∙4 =16б)4∙3 =12а)4∙5∙5 = 100б)4∙4∙3 =48а)(9∙8∙7 ∙6):24 = 945а)(7∙6):2 = 21
- 40. Домашнее задание№504,№505,№507
- 41. Используемые ресурсы:1. Портрет Лейбница http://ru.wikipedia.org/wiki/ 2.Слайд 6,13
Слайд 2 Комбинаторика – это область математики, изучающая вопрос, сколько разных
Комбинаторика
Слайд 3Готфрид Лейбниц
Истоки этой науки были положены знаменитым немецким математиком
(1646-1716)
Слайд 4Правило умножения
Пусть объект А выбирается n способами, объект В выбирается
пару объектов (А,В) можно выбрать n • m способами.
Все очень просто – каждый из n способов выбора объекта А комбинируется с каждым из m способов выбора объекта В, то есть количество способов просто умножается друг на друга.
Слайд 5№492
1способ:
составить дерево возможных вариантов
2 способ:
решить задачу, используя
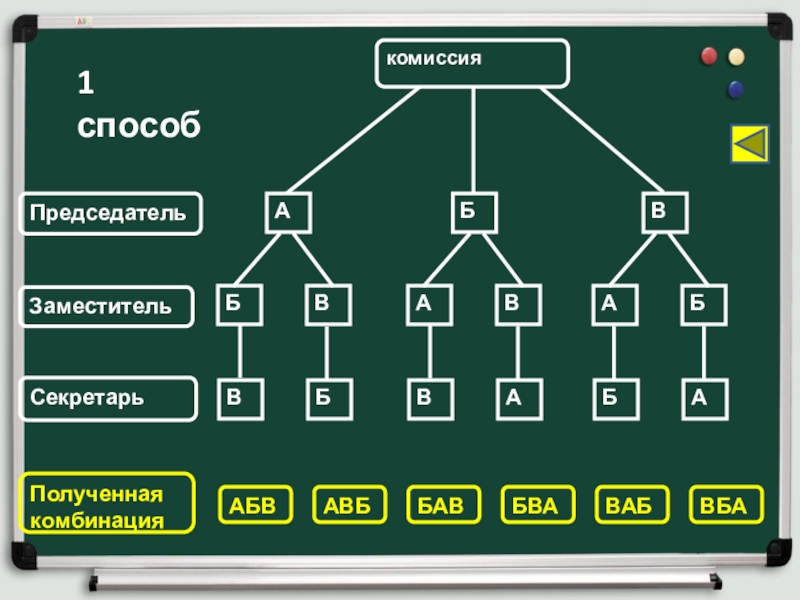
Собрание для проведения тайного голосования по важному вопросу избрало счетную комиссию, в состав которой вошли Антонов, Борисова и Ващенко. Члены счетной комиссии должны распределить обязанности: председатель, заместитель, секретарь. Сколькими способами они могут это сделать?
Слайд 6Председатель
Заместитель
Секретарь
комиссия
А
Полученная
комбинация
АБВ
АВБ
БАВ
БВА
ВАБ
ВБА
Б
В
Б
В
А
В
А
Б
В
Б
В
А
Б
А
1 способ
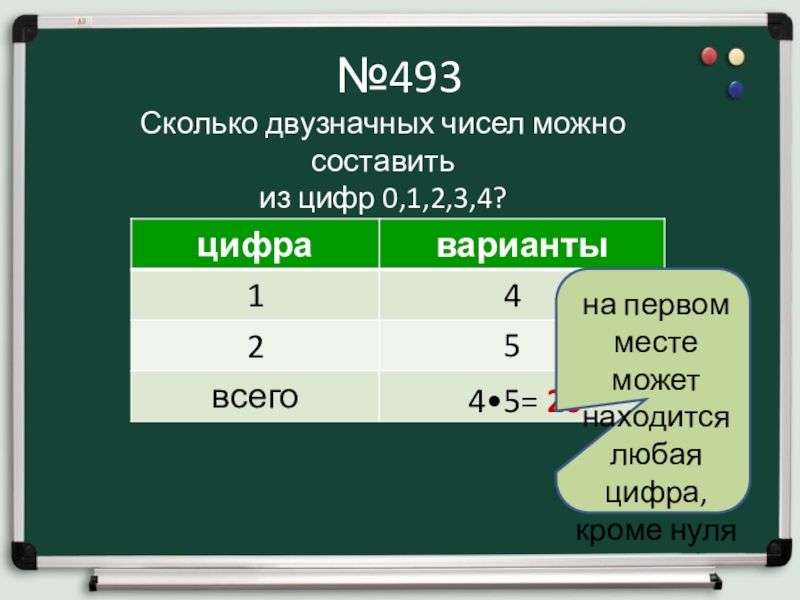
Слайд 8№493
Сколько двузначных чисел можно составить
из цифр 0,1,2,3,4?
4•5= 20
4
5
на первом месте
Слайд 9№494
1)Сколько трехзначных чисел можно составить из
цифр1,3,5,7 ?
2) Сколько трехзначных
1,3,5,7,если известно, что цифры не должны
повторяться?
4
4
4
4•4•4= 64
4
3
2
4•3•2= 24
Слайд 10№495
Несколько стран решили использовать для своего государственного флага символику в виде
3•2•1= 6
3
2
1
Слайд 11№496
Несколько стран решили использовать для своего государственного флага символику в виде
4
3
2
1
4•3•2•1= 24
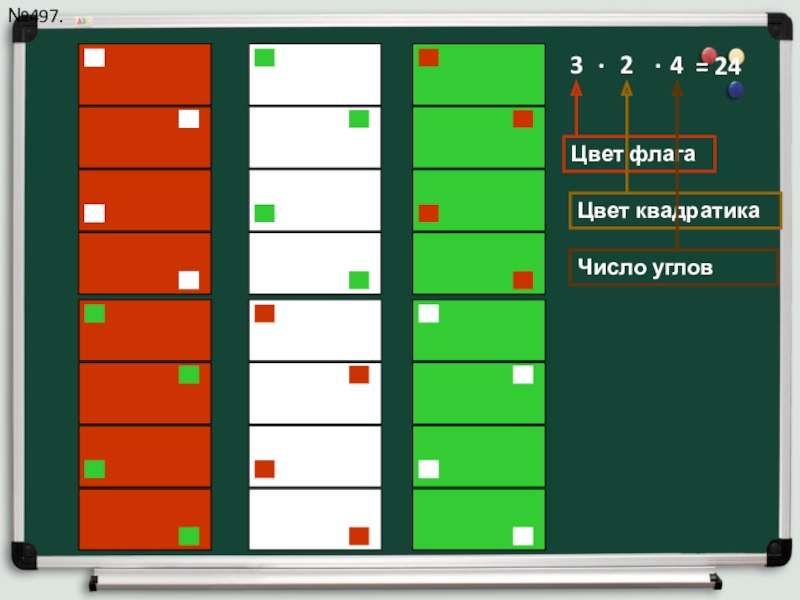
Слайд 12№497
Руководство некоторой страны решило сделать свой государственный флаг таким: на одноцветном
3•2•4= 24
3
2
4
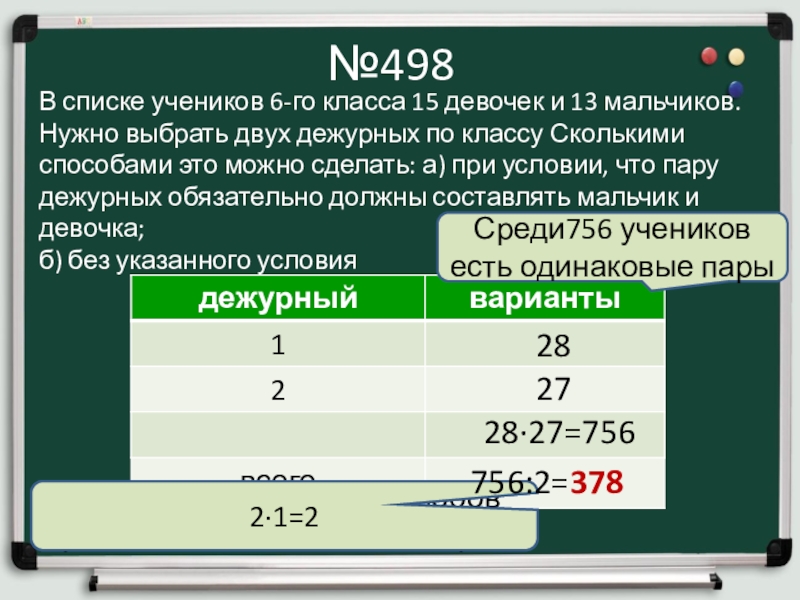
Слайд 14№498
В списке учеников 6-го класса 15 девочек и 13 мальчиков. Нужно
б) без указанного условия
15
13
15•13= 195
28
27
28∙27=756
Среди756 учеников есть одинаковые пары
Сколько существует способов расположения девочек в паре?
2∙1=2
756:2=378
Слайд 15№499а)
В списке учеников 6 класса 15 девочек и 13 мальчиков.Нужно выделить
а) все члены группы девочки;
Ответ: 455 способов
1)15∙14∙13=2730(способов)-выбрать с повторением тройки девочек
2)3∙2∙1=6(способов)-расположения девочек по порядку в каждой тройке
3)2730:6=455(способов)-выбрать без учета порядка тройку девочек
Слайд 16№499б)
В списке учеников 6 класса 15 девочек и 13 мальчиков. Нужно
б) все члены группы- мальчики;
1)12∙11∙10=1320(способов)-выбрать с повторением тройку мальчиков
2)3 ∙ 2∙1=6(способов)-расположения мальчиков по порядку в каждой тройке
3)1320:6= 220(способов)- выбрать без учета порядка тройку мальчиков
Ответ: 220 способов
Слайд 17№499в
В списке учеников 6 класса 15 девочек и 13 мальчиков. Нужно
в) в группе 1 девочка и 2 мальчика;
1)12∙11=132(способа)-выбрать с повторением пару мальчиков
2)2∙1=2(способа)-расположения мальчиков по порядку в каждой паре
3)132:2=66(способ)-выбрать без учета порядка пару мальчиков
4)15 ∙ 66=990(способ)-выбрать без учета порядка 1девочку и 2 мальчиков
Ответ: 990 способа
Слайд 18№499 г)
В списке учеников 6 класса 15 девочек и 13 мальчиков.
г) в группе 2 девочки и 1 мальчик;
1)15∙14=210(способов)-выбрать с повторением пару девочек
2)2∙1=2(способа)-расположения девочек по порядку в каждой паре
3)210:2=105(способов)-выбрать без учета порядка пару девочек
4)105 ∙ 12=1260(способа)-выбрать без учета порядка 2девочек и 1 мальчика
Ответ: 1260 способов
Слайд 19При решении этой задачи надо учесть, что 1 мальчик из класса
Слайд 20№500а,б
В списке учеников 6 класса 15 девочек и 13 мальчиков. Нужно
а) все члены группы девочки;
(14∙13 ∙ 12):6=364(способа)-выбрать без учета порядка тройку девочек
б) все члены группы- мальчики;
(13∙12 ∙ 11):6=286(способа)-выбрать без учета порядка тройку девочек
Слайд 21№500в)г)
В списке учеников 6 класса 15 девочек и 13 мальчиков. Нужно
в) в группе 1 девочка и 2 мальчика;
(13∙12):2 ∙ 14= 1092(способа)-выбрать без учета порядка 1 девочку и 2 мальчиков
г) в группе 2 девочки и 1 мальчик;
(14∙13 ):2 ∙ 13=1183(способа)-выбрать без учета порядка 2девочки и 1 мальчикадевочек
Слайд 22№501
а) Сколько двузначных чисел можно составить из
цифр 1,2,3,4,5
б) Сколько
из цифр 1,2,3,4,5 при условии, что цифры не
должны повторяться?
5∙5= 25 двузначных чисел можно составить с повторением цифр
5∙4 = 20 двузначных можно составить без повторения цифр
Слайд 23№502
а) Сколько трехзначных чисел можно составить
из цифр 2,4,5?
3
повторением цифр
б) Сколько трехзначных чисел можно составить
из цифр 2,4,5, при условии, что цифры не
должны повторяться?
3 ∙ 2 ∙ 1=6 трехзначных чисел можно составить без повторения цифр
Слайд 24 Ответ б)
Ответ а)
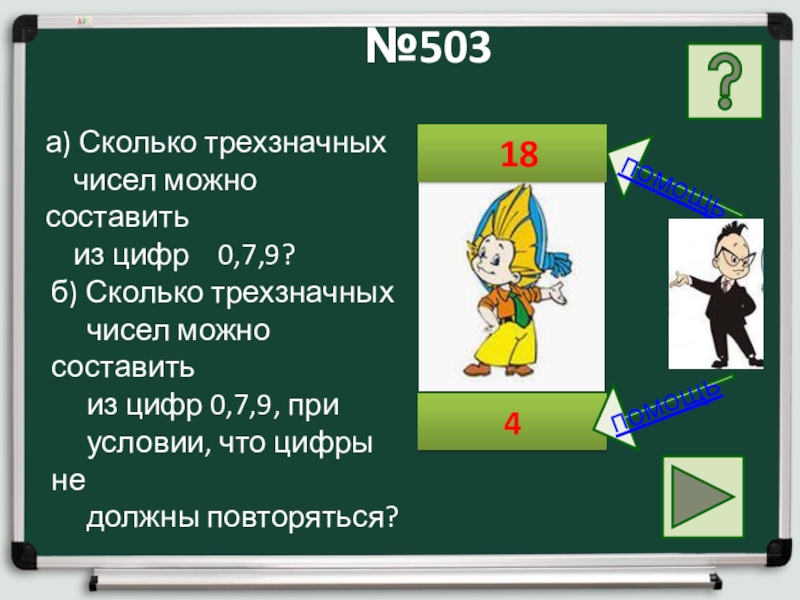
№503
а) Сколько трехзначных
чисел
из цифр 0,7,9?
б) Сколько трехзначных
чисел можно составить
из цифр 0,7,9, при
условии, что цифры не
должны повторяться?
помощь
4
помощь
Слайд 28№506
В 6 а классе в четверг 5 уроков: математика, информатика, русский
Сколько имеется вариантов расписания при условии, что физкультура- последний урок?
Сколько имеется вариантов расписания при условии, что физкультура- последний урок, а математика -первый?
5 ∙4∙3∙2∙1 = 120
4 ∙3∙2∙1∙1 = 24
1 ∙3∙2∙1∙1 = 6
Слайд 29№508
В чемпионате России по футболу в высшей лиге участвуют 16 команд.
интернет-вопрос читателей, задав им два вопроса:
1) Какие три команды станут призерами чемпионата, т.е. займут первое, второе и третье места?
2)Какие две команды займут два последних места?
а) Сколько вариантов состава призеров чемпионата?
б) Сколько вариантов состава неудачников чемпионата?
16 ∙15∙14 = 3360
16 ∙15 = 240
Слайд 30№509а
В двух урнах имеется по семь шаров, в каждой - семи
а) Сколько существует комбинаций, при которых
вынутые шары одного цвета?
1
2
7
1
Итого
7∙1=7
Слайд 31№509б
В двух урнах имеется по семь шаров, в каждой - семи
б ) Сколько существует комбинаций, при которых
вынутые шары разных цветов?
1)7∙6=42 (способа)-выбрать с повторением пару шаров
2) 2∙1=2(способа)-расположения шаров по порядку
в каждой паре
42:2 =21(способ)-выбрать без учета порядка два шара разного цвета
Слайд 32№509в
В двух урнах имеется по семь шаров, в каждой - семи
в) Сколько существует различных комбинаций вынутых шаров(комбинации типа"белый-красный"и "красный -белый" считаются одинаковыми)?
(7∙6):2 =21(способ)-выбрать без учета порядка два шара разного цвета
7∙1=7(способов) –выбрать пару одинакового цвета
Итого: 21+7 =28(способов)–различных пар шаров
Слайд 33Самостоятельная работа
1. Сколько двузначных чисел можно составить из цифр 1,2,6 при
а) цифры могут повторяться;
б) цифры не должны повторяться?
1. Сколько двузначных чисел можно составить из цифр 2,5,4,7 при условии, что:
а) цифры могут повторяться;
б) цифры не должны повторяться?
Вариант 1
Вариант 2
Слайд 34Самостоятельная работа
Вариант 1
Вариант 2
2. Сколько трехзначных чисел можно составить из цифр
а) цифры могут повторяться;
б) цифры не должны повторяться?
2. Сколько трехзначных чисел можно составить из цифр 0,5,4,8,6 при условии, что:
а) цифры могут повторяться;
б) цифры не должны повторяться?
Слайд 35Самостоятельная работа
Вариант 1
Вариант 2
3. В списке баскетбольной команды 20 человек. Из
а) Сколькими способами из этих игроков можно составить тройку нападающих?
б) Сколькими способами из этих игроков можно составить пару защитников?
3. В списке футбольной команды 22 человека. Из них 9 играют в нападении, а 7 - в защите
а) Сколькими способами из этих игроков можно составить четверку нападающих?
б) Сколькими способами из этих игроков можно составить пару защитников?
Разбор задач
Взаимопроверка
Слайд 36Разберем решение задач:
1. Сколько двузначных чисел можно составить из цифр 1,2,6
1. Сколько двузначных чисел можно составить из цифр 2,5,4,7 при условии, что:
а) цифры могут повторяться
а) цифры могут повторяться
б) цифры не повторяются?
3∙3=9
3∙2=6
4∙4=16
б) цифры не повторяются?
4∙3=12
Вариант 1
Вариант 2
Слайд 37Решение
2. Сколько трехзначных чисел можно составить из цифр 0,1,2,6 при условии,
Вариант 1
Вариант 2
2. Сколько трехзначных чисел можно составить из цифр 0,5,4,8,6 при условии, что:
а) цифры могут повторяться
а) цифры могут повторяться
3∙4∙4=48
4∙5∙5 =100
б) цифры не повторяются?
б) цифры не повторяются?
3∙3∙2 =18
4∙4∙3 =48
Слайд 38Решение
Вариант 1
Вариант 2
3.В списке баскетбольной команды 20 человек. Из них 12
3. В списке футбольной команды 22 человека. Из них 9 играют в нападении, а 7 - в защите
а) Сколькими способами из этих игроков можно составить тройку нападающих?
б) Сколькими способами из этих игроков можно составить пару защитников?
а) Сколькими способами из этих игроков можно составить четверку нападающих?
б) Сколькими способами из этих игроков можно составить пару защитников?
(12∙11∙10):6=48
(8∙7):2=28
(9∙8∙7∙6):24 =945
(7∙6):2=21
Слайд 39Ответы
1
2
3
а)3∙3=9
б)3∙2=6
а)3∙4∙4=48
б)3∙3∙2 =18
а)(12∙11∙10):6=48
б)(8∙7):2=28
а)4∙4 =16
б)4∙3 =12
а)4∙5∙5 = 100
б)4∙4∙3 =48
а)(9∙8∙7 ∙6):24 =
а)(7∙6):2 = 21
Слайд 41Используемые ресурсы:
1. Портрет Лейбница http://ru.wikipedia.org/wiki/
2.Слайд 6,13 http://school-collection.edu.ru
https://www.google.ru/
http://images.yandex.ru/
4. Книга
3. Незнайка,
5. Источник шаблона презентации:
Татарников Виталий Викторович
учитель физики МОУ СОШ №20
п. Баранчинский, г. Кушва, Свердловской обл.
Рисунок для фона http://17986.globalmarket.com.ua/data/530378_3.jpg
http://pedsovet.su/
6.И.И. Зубарева, А.Г. Мордкович. Математика. 6 класс. Учебник