Учитель математики
ГБОУ СОШ № 390
Лаврентьева И. А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Геометрические тела и их применение
Содержание
- 1. Геометрические тела и их применение
- 2. планиметрия – это раздел геометрии, изучающий геометрические фигуры на плоскости
- 3. АКСИОМА – УТВЕРЖДЕНИЕ, ПРИНИМАЮЩЕЕСЯ КАК ИСТИННОЕ, БЕЗ ДОКАЗАТЕЛЬСТВ.АКСИОМЫ ПЛАНИМЕТРИИ – ЭТО ОСНОВНЫЕ СВОЙСТВА ПРОСТЕЙШИХ ГЕОМЕТРИЧЕСКИХ ФИГУР
- 4. НЕОПРЕДЕЛЯЕМЫЕ ИЛИ ОСНОВНЫЕ ПОНЯТИЯ В ПЛАНИМЕТРИИ-ТОЧКА,ПРЯМАЯОСНОВНЫЕ ФИГУРЫ
- 5. ВИДЫ АКСИОМ ПЛАНИМЕТРИИ
- 6. АКСИОМЫ ПРИНАДЛЕЖНОСТИ1. Какова бы ни была прямая,
- 7. А АКСИОМЫ РАСПОЛОЖЕНИЯксиомы расположения.1.
- 8. АКСИОМЫ ИЗМЕРЕНИЯКаждый отрезок имеет определённую длину,
- 9. АКСИОМЫ ОТКЛАДЫВАНИЯ1. На любой полупрямой от её
- 10. АКСИОМЫ ОТКЛАДЫВАНИЯКаков бы ни был треугольник, существует
- 11. АКСИОМА ПАРАЛЛЕЛЬНОСТИ Через точку, не лежащую
планиметрия – это раздел геометрии, изучающий геометрические фигуры на плоскости
Слайд 3АКСИОМА – УТВЕРЖДЕНИЕ, ПРИНИМАЮЩЕЕСЯ КАК ИСТИННОЕ,
БЕЗ ДОКАЗАТЕЛЬСТВ.
АКСИОМЫ ПЛАНИМЕТРИИ – ЭТО
ОСНОВНЫЕ СВОЙСТВА ПРОСТЕЙШИХ ГЕОМЕТРИЧЕСКИХ ФИГУР
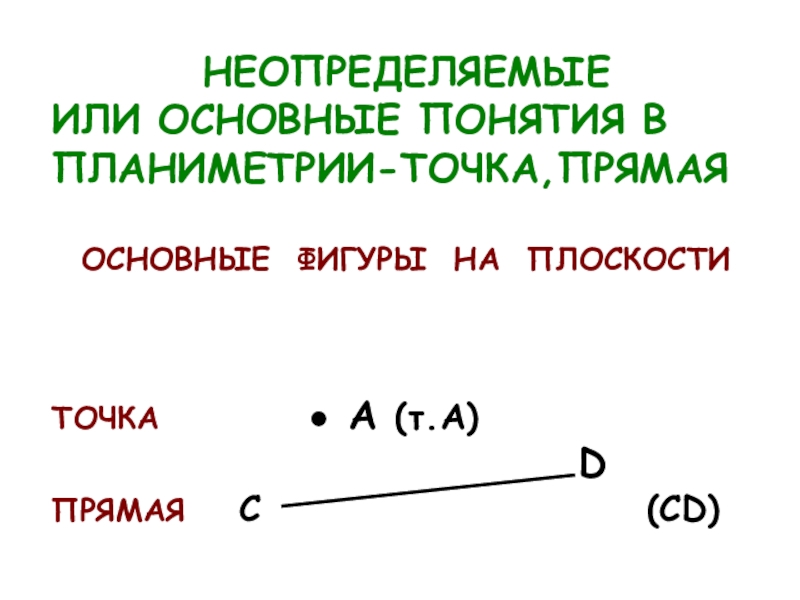
Слайд 4НЕОПРЕДЕЛЯЕМЫЕ
ИЛИ ОСНОВНЫЕ ПОНЯТИЯ В ПЛАНИМЕТРИИ-ТОЧКА,ПРЯМАЯ
ОСНОВНЫЕ ФИГУРЫ НА ПЛОСКОСТИ
ТОЧКА
А (т.А)
D
ПРЯМАЯ C (CD)
D
ПРЯМАЯ C (CD)
Слайд 5ВИДЫ
АКСИОМ ПЛАНИМЕТРИИ
Аксиомы откладывания
Аксиома параллельности
Аксиомы принадлежности
Аксиомы расположения
Аксиомы измерения
Аксиома параллельности
Аксиомы принадлежности
Аксиомы расположения
Аксиомы измерения
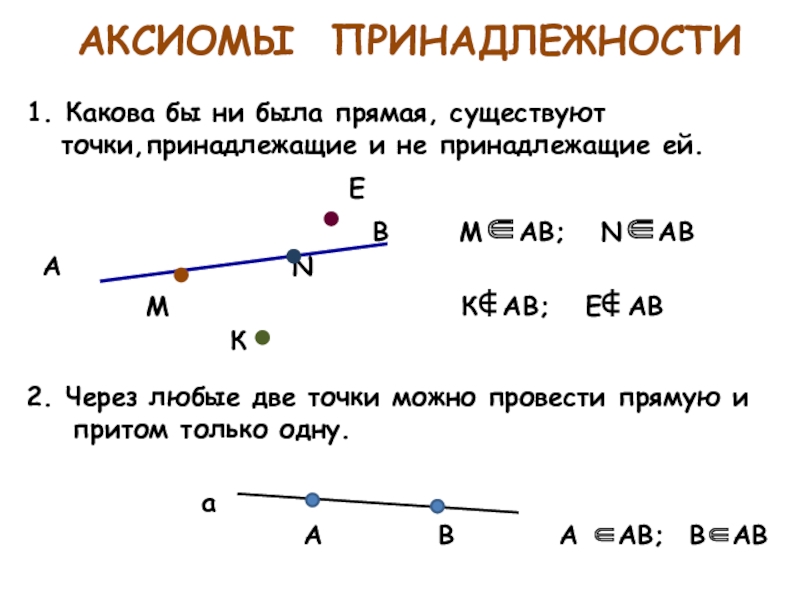
Слайд 6АКСИОМЫ ПРИНАДЛЕЖНОСТИ
1. Какова бы ни была прямая, существуют
точки,принадлежащие и не принадлежащие ей.
E
В МАВ; NАВ
А N
М К АВ; E АВ
К
2. Через любые две точки можно провести прямую и притом только одну.
а
А В А АВ; BАВ
E
В МАВ; NАВ
А N
М К АВ; E АВ
К
2. Через любые две точки можно провести прямую и притом только одну.
а
А В А АВ; BАВ
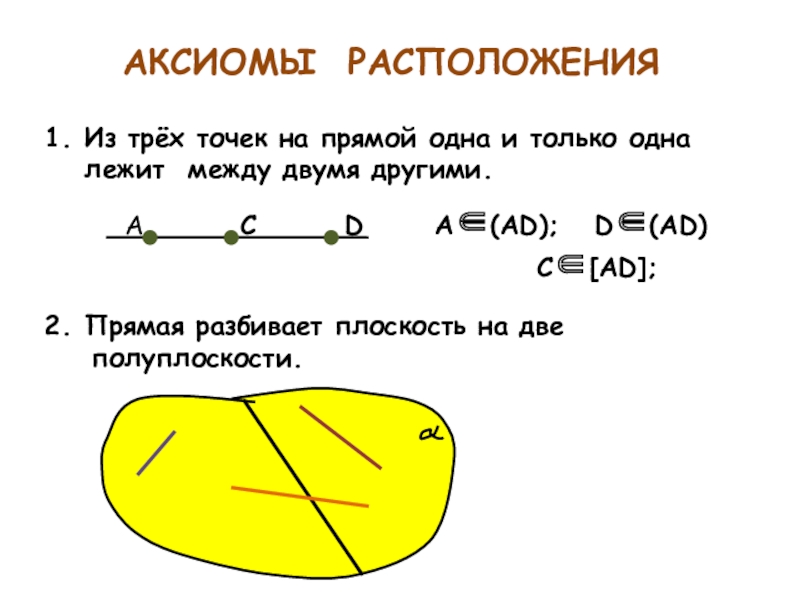
Слайд 7А АКСИОМЫ РАСПОЛОЖЕНИЯ
ксиомы расположения.
1. Из трёх точек на
прямой одна и только одна лежит между двумя другими.
А С D A(АD); D(АD)
CАD;
2. Прямая разбивает плоскость на две полуплоскости.
А С D A(АD); D(АD)
CАD;
2. Прямая разбивает плоскость на две полуплоскости.
Слайд 8АКСИОМЫ ИЗМЕРЕНИЯ
Каждый отрезок имеет определённую длину,
большую нуля. Длина отрезка равна
сумме длин
частей, на которые он разбивается любой его
точкой.
BАC
A B C АC=AB+BC
2. Каждый угол имеет опредённую градусную меру,
Большую нуля. Развёрнутый угол равен 180о. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящем между его сторонами.
M
A B C D E F
ABC=180 DEF= DEM + MEF
BАC
A B C АC=AB+BC
2. Каждый угол имеет опредённую градусную меру,
Большую нуля. Развёрнутый угол равен 180о. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящем между его сторонами.
M
A B C D E F
ABC=180 DEF= DEM + MEF
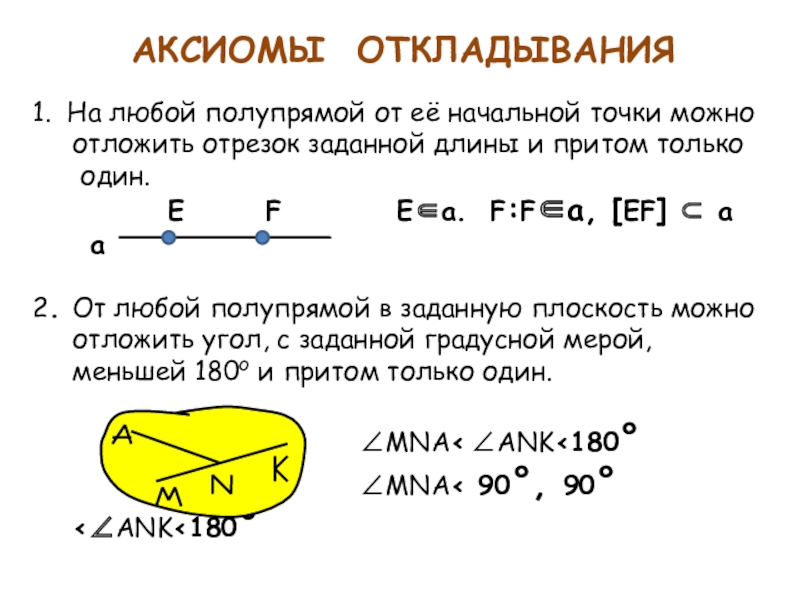
Слайд 9АКСИОМЫ ОТКЛАДЫВАНИЯ
1. На любой полупрямой от её начальной точки можно
отложить отрезок заданной длины и притом только
один.
Е F Ea. F:Fa, EF a
a
2. От любой полупрямой в заданную плоскость можно отложить угол, с заданной градусной мерой, меньшей 180о и притом только один.
MNA ANK180
MNA 90, 90ANK180
Е F Ea. F:Fa, EF a
a
2. От любой полупрямой в заданную плоскость можно отложить угол, с заданной градусной мерой, меньшей 180о и притом только один.
MNA ANK180
MNA 90, 90ANK180
Слайд 10АКСИОМЫ ОТКЛАДЫВАНИЯ
Каков бы ни был треугольник, существует
треугольник, равный ему, в
заданном расположении
относительно данной полупрямой.
AMN = AMN
AMN = AMN
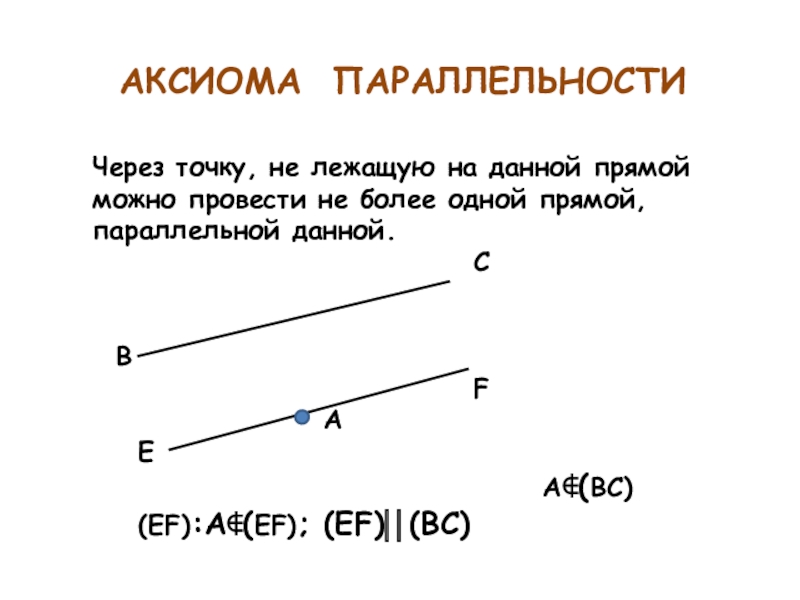
Слайд 11АКСИОМА ПАРАЛЛЕЛЬНОСТИ
Через точку, не лежащую на данной прямой
можно провести не более одной прямой,
параллельной данной.
C
B
F
A
E
A(ВC)
(EF):A(EF); (EF)(BC)
C
B
F
A
E
A(ВC)
(EF):A(EF); (EF)(BC)