Выполнил: Карпачев Дмитрий,
ученик 7 Д класса.
Руководитель: Долженко Т.К.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему ФИГУРНЫЕ ЧИСЛА В ЖИЗНИ ЧЕЛОВЕКА
Содержание
- 1. ФИГУРНЫЕ ЧИСЛА В ЖИЗНИ ЧЕЛОВЕКА
- 2. «Знания лишь тем открываются, кто с разными числами знается!»Пифагор
- 3. Рассмотреть историю возникновения фигурных чисел.
- 4. Из истории фигурных чисел Впервые фигурные числа
- 5. В таком виде, пользуясь камешками, древние
- 6. Изучением фигурных чисел увлеклись Блез Паскаль и Пьер ФермаБлез ПаскальПьер Ферма
- 7. Виды фигурных чиселЛинейныеПлоскиеТреугольныеКвадратныеПятиугольныеТелесные числаШестиугольныеТетраэдрическиеЦентрированные восьмиугольныеКвадратные пирамидальные
- 8. Линейные числаПростые числа, которые нельзя разложить на
- 9. Плоские числаМожно представить в виде произведения двух
- 10. Треугольные числаЭто число кружков, которые могут быть расставлены в форме правильного треугольника.(n(n+1))/2n - порядковое число
- 11. Квадратные числаКвадратное число - это число, которое представляет собой квадрат любого числа:2*2, 3*3, 4*4 и т.д.
- 12. Пятиугольные числа1, 5, 12, 22, 35, 51,
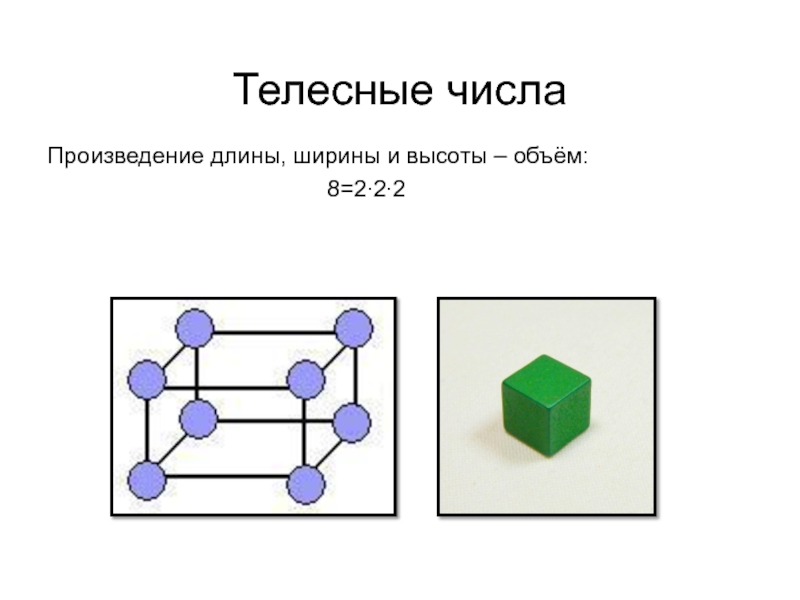
- 13. Телесные числаПроизведение длины, ширины и высоты – объём:8=2∙2∙2
- 14. Шестиугольные числа Шестиугольное число
- 15. Тетраэдрические числаПредставляют пирамиду, в основании которой лежит
- 16. Центрированные восьмиугольные числа Восьмиугольник с точкой в
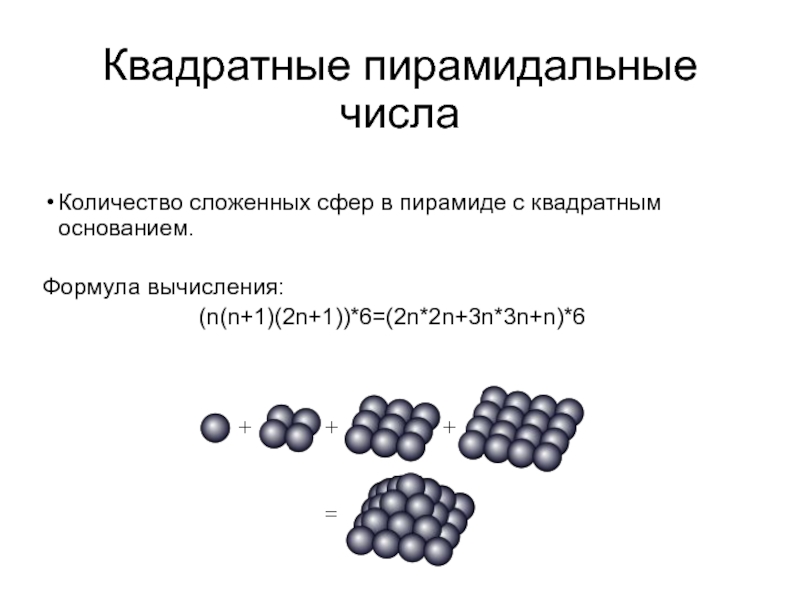
- 17. Квадратные пирамидальные числаКоличество сложенных сфер в пирамиде с квадратным основанием. Формула вычисления:(n(n+1)(2n+1))*6=(2n*2n+3n*3n+n)*6
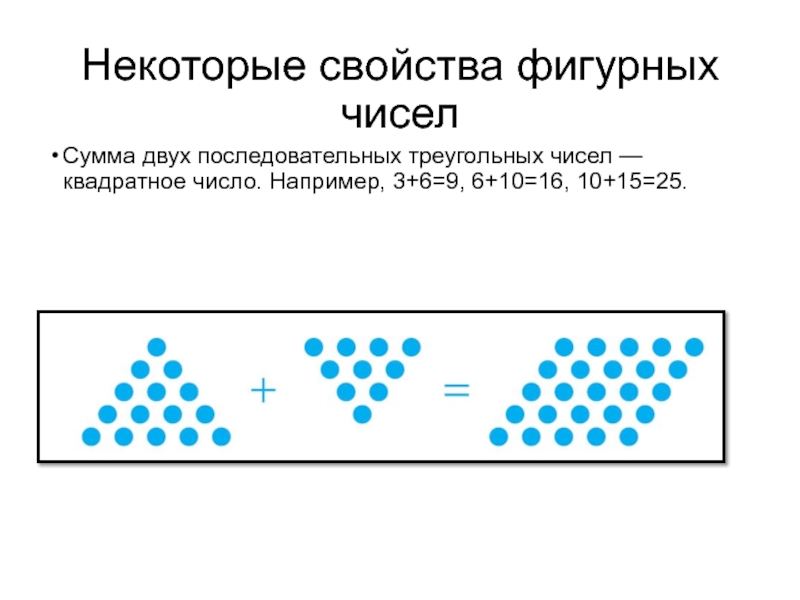
- 18. Некоторые свойства фигурных чиселСумма двух последовательных треугольных чисел — квадратное число. Например, 3+6=9, 6+10=16, 10+15=25.
- 19. Кто занимается фигурными числами сейчасФигурными числами занимается
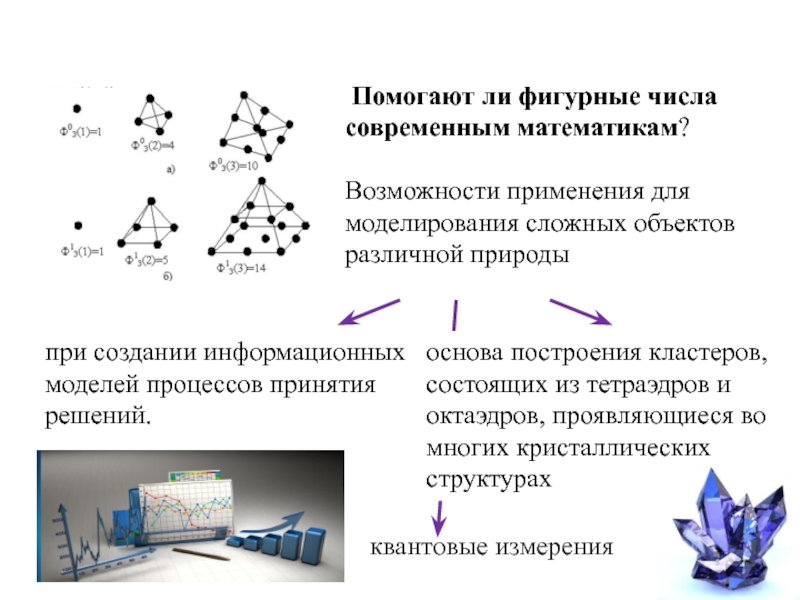
- 20. Помогают ли фигурные числа современным математикам?Возможности
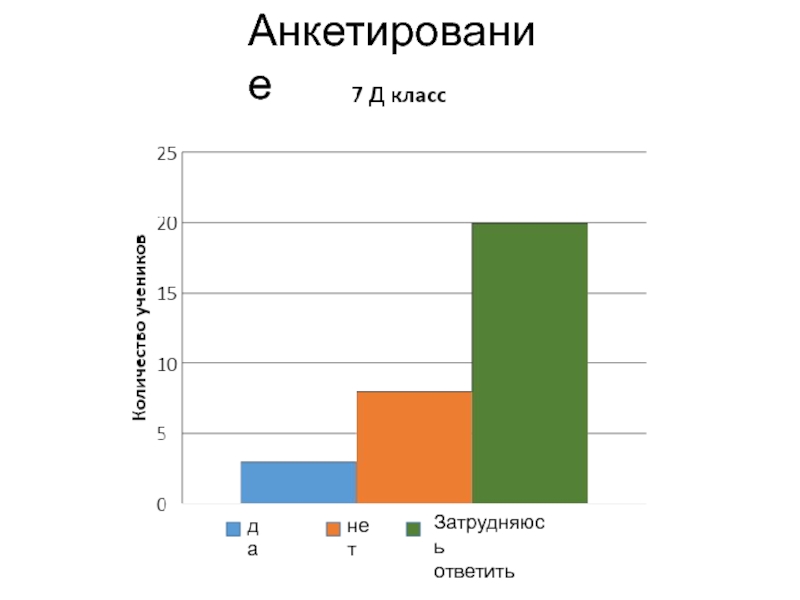
- 21. Анкетирование
- 22. Применение фигурных чисел в нашей жизни
- 23. Применение фигурных чисел в нашей жизни
- 24. Применение фигурных чисел в нашей жизни
- 25. Применение фигурных чисел в нашей жизниНеокуб
- 26. Компактное хранение и простой подсчет
- 27. Фигурные числа на детской площадке
- 28. Слайд 28
- 29. Заключение «Часто говорят, что цифры управляют миром;
- 30. Спасибо за внимание!
«Знания лишь тем открываются, кто с разными числами знается!»Пифагор
Слайд 1 МАОУ СОШ № 8 имени генерал-лейтенанта В.Г. Асапова. Фигурные числа в жизни
человека
Слайд 3 Рассмотреть историю возникновения фигурных чисел.
Рассмотреть виды фигурных
чисел
Рассмотреть возможности применения фигурных чисел в повседневной жизни (в живописи, архитектуре, дизайне)
Методы исследования:
обработка и анализ научных источников
анализ научной литературы и пособий по исследуемой проблеме.
Рассмотреть возможности применения фигурных чисел в повседневной жизни (в живописи, архитектуре, дизайне)
Методы исследования:
обработка и анализ научных источников
анализ научной литературы и пособий по исследуемой проблеме.
Целью работы является более глубоко изучить и исследовать одно из понятий математики – фигурное число.
Выявить его роль в нашей жизни.
В соответствии с поставленной целью решались следующие задачи:
Слайд 4Из истории фигурных чисел
Впервые фигурные числа были определены пифагорейцами в IV-VI
веке до н. э.
Первый упоминание в книге «Начала» Евклида.
Многие теоремы о многоугольных числах доказывали Ферма (ХVII в.), Эйлер и Лагранж.
Первый упоминание в книге «Начала» Евклида.
Многие теоремы о многоугольных числах доказывали Ферма (ХVII в.), Эйлер и Лагранж.
Слайд 5
В таком виде, пользуясь камешками, древние греки и египтяне использовали
числа.
Числа были в виде геометрических фигур. Так возник термин «фигурные числа».
Числа были в виде геометрических фигур. Так возник термин «фигурные числа».
Слайд 7Виды фигурных чисел
Линейные
Плоские
Треугольные
Квадратные
Пятиугольные
Телесные числа
Шестиугольные
Тетраэдрические
Центрированные восьмиугольные
Квадратные пирамидальные
Слайд 8Линейные числа
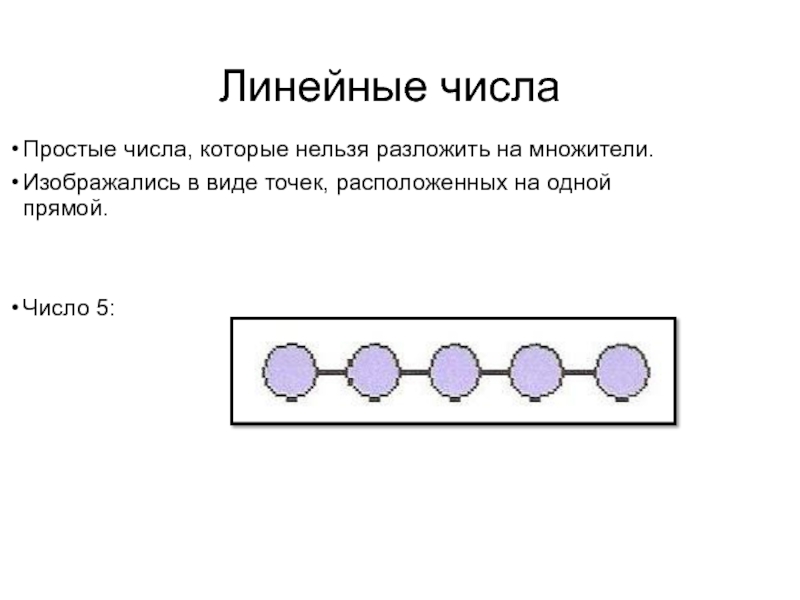
Простые числа, которые нельзя разложить на множители.
Изображались в виде
точек, расположенных на одной прямой.
Число 5:
Число 5:
Слайд 9Плоские числа
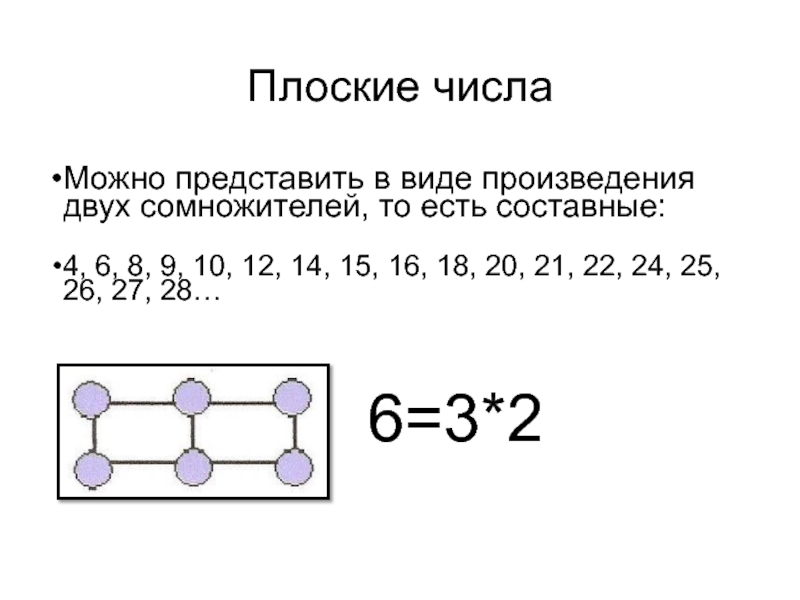
Можно представить в виде произведения двух сомножителей, то есть составные:
4, 6,
8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28…
6=3*2
Слайд 10Треугольные числа
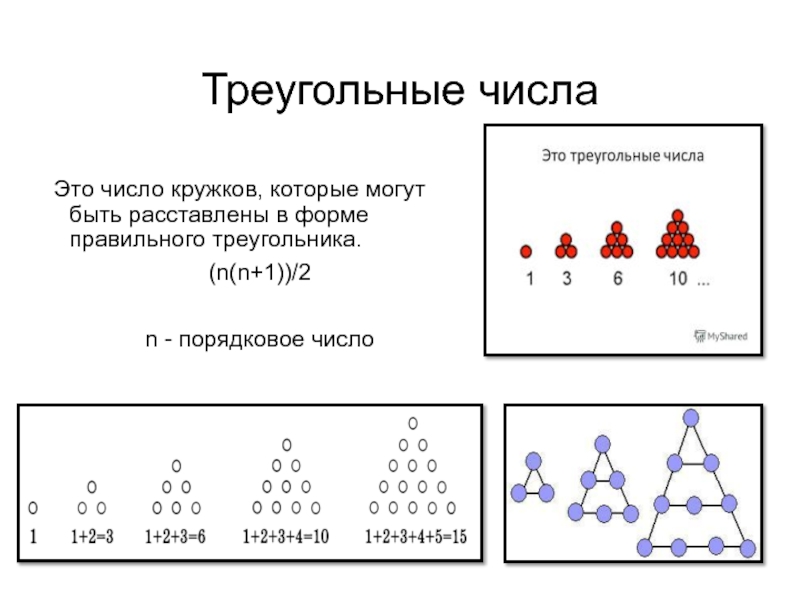
Это число кружков, которые могут быть расставлены в форме правильного
треугольника.
(n(n+1))/2
n - порядковое число
(n(n+1))/2
n - порядковое число
Слайд 11Квадратные числа
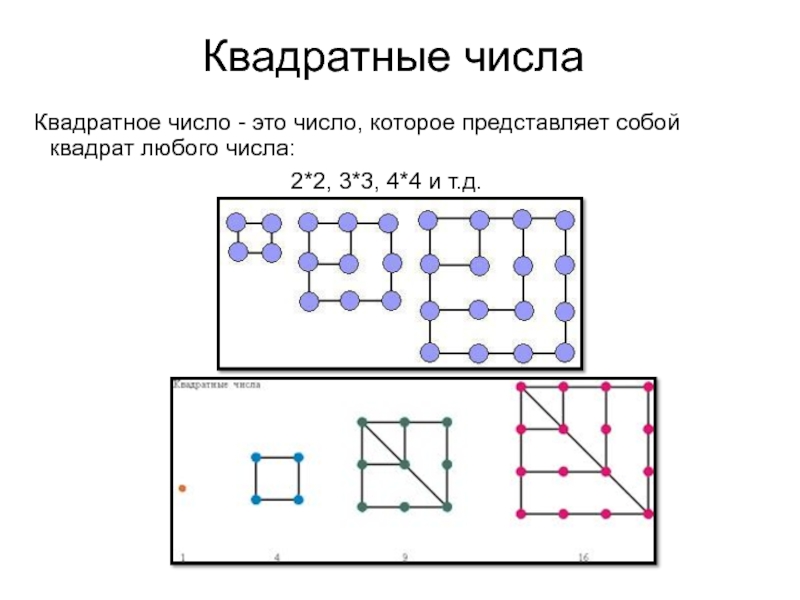
Квадратное число - это число, которое представляет собой квадрат любого
числа:
2*2, 3*3, 4*4 и т.д.
2*2, 3*3, 4*4 и т.д.
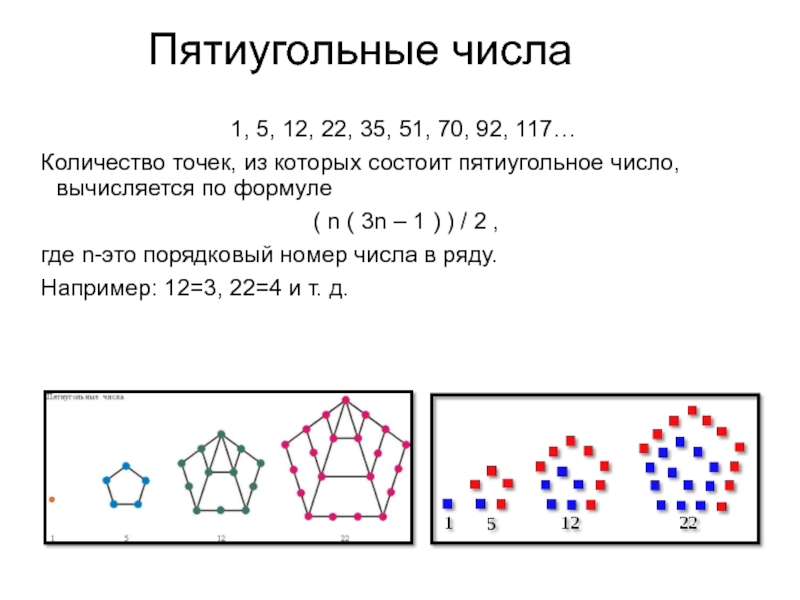
Слайд 12Пятиугольные числа
1, 5, 12, 22, 35, 51, 70, 92, 117…
Количество
точек, из которых состоит пятиугольное число, вычисляется по формуле
( n ( 3n – 1 ) ) / 2 ,
где n-это порядковый номер числа в ряду.
Например: 12=3, 22=4 и т. д.
( n ( 3n – 1 ) ) / 2 ,
где n-это порядковый номер числа в ряду.
Например: 12=3, 22=4 и т. д.
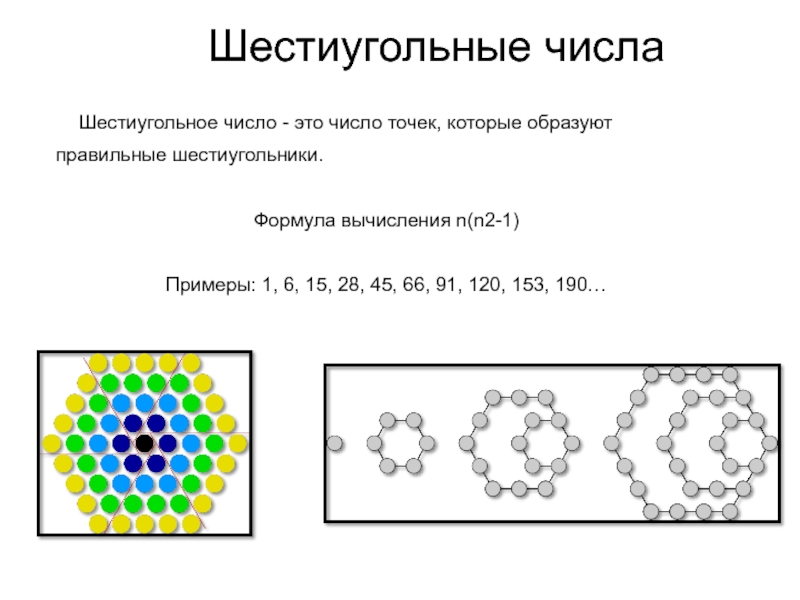
Слайд 14Шестиугольные числа
Шестиугольное число - это число точек,
которые образуют правильные шестиугольники.
Формула вычисления n(n2-1)
Примеры: 1, 6, 15, 28, 45, 66, 91, 120, 153, 190…
Формула вычисления n(n2-1)
Примеры: 1, 6, 15, 28, 45, 66, 91, 120, 153, 190…
Слайд 15Тетраэдрические числа
Представляют пирамиду, в основании которой лежит треугольник:
Формула вычисления
(n(n+1)(2n+1))/6
Пример:
1, 4, 10, 20, 35, 56, 84, 120
(n(n+1)(2n+1))/6
Пример:
1, 4, 10, 20, 35, 56, 84, 120
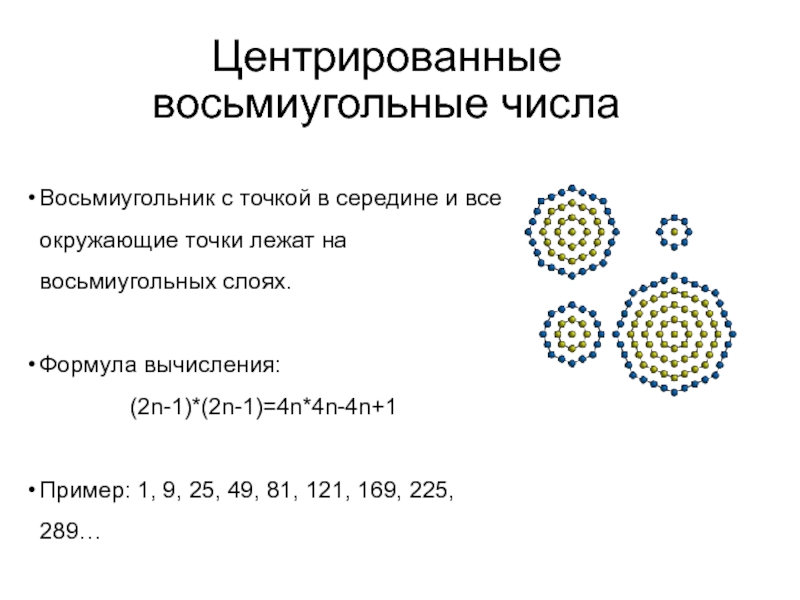
Слайд 16Центрированные восьмиугольные числа
Восьмиугольник с точкой в середине и все окружающие точки
лежат на восьмиугольных слоях.
Формула вычисления:
(2n-1)*(2n-1)=4n*4n-4n+1
Пример: 1, 9, 25, 49, 81, 121, 169, 225, 289…
Формула вычисления:
(2n-1)*(2n-1)=4n*4n-4n+1
Пример: 1, 9, 25, 49, 81, 121, 169, 225, 289…
Слайд 17Квадратные пирамидальные числа
Количество сложенных сфер в пирамиде с квадратным основанием.
Формула вычисления:
(n(n+1)(2n+1))*6=(2n*2n+3n*3n+n)*6
Слайд 18Некоторые свойства фигурных чисел
Сумма двух последовательных треугольных чисел — квадратное число.
Например, 3+6=9, 6+10=16, 10+15=25.
Слайд 19Кто занимается фигурными числами сейчас
Фигурными числами занимается Елена Ивановна Деза -
доктор педагогических наук, соавтор книги «Фигурные числа»
Слайд 20 Помогают ли фигурные числа современным математикам?
Возможности применения для моделирования сложных
объектов различной природы
при создании информационных моделей процессов принятия решений.
основа построения кластеров, состоящих из тетраэдров и октаэдров, проявляющиеся во многих кристаллических структурах
квантовые измерения
Слайд 29Заключение
«Часто говорят, что цифры управляют миром; по крайней мере нет
сомнения в том, что цифры показывают, как он управляется.» (И. Гете)
Вычислять в «уме»
Понять законы умножения
Границы применения в науке расширяются
Займут достойное место в дизайне
Они завораживающе красивы
