- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Дискретные случайные величины
Содержание
- 1. Дискретные случайные величины
- 2. Цель занятия:Познакомиться с понятием дискретной случайной величины,
- 3. Случайное событие, связанное с некоторым опытом, является
- 4. Определение 1. Случайной называется величина, которая в
- 5. Пример 1. Игрок бросает монету – при
- 6. Пример 3. Эксперимент – n-кратное повторение опыта
- 7. Пример 5. Эксперимент – случайный выбор точки
- 8. Определение 2. Случайная величина называется дискретной, если
- 9. Определение 3. Соответствие между возможными значениями х1,
- 10. События Х = х1, Х = х2,
- 11. Пример. Бросаются две правильные однородные монеты. Сколько из них выпадет гербом кверху?
- 12. Над случайными величинами устанавливаются операции сложения и
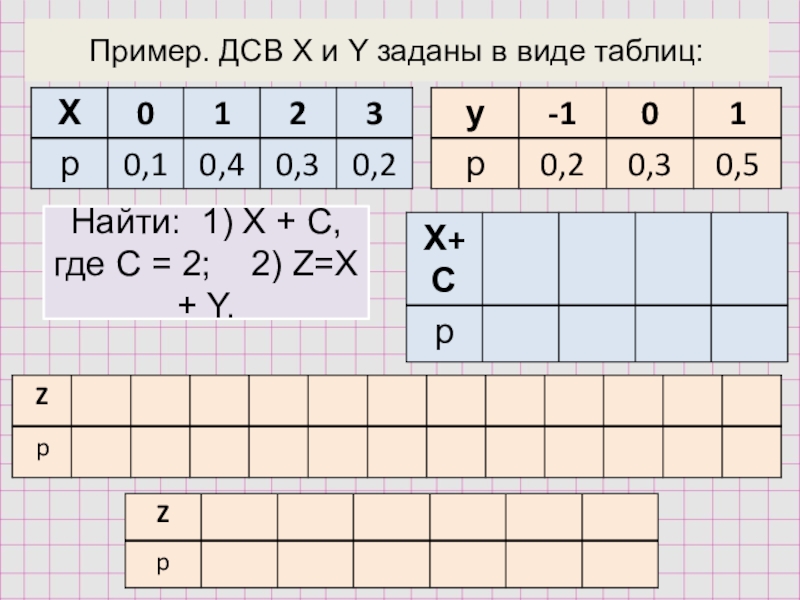
- 13. Пример. ДСВ X и Y заданы в
- 14. Биномиальное распределениеПусть случайная величина Х – число
- 15. Определение. Биномиальным распределением называется закон распределения случайной
- 16. Пример. Монета бросается 5 раз, представим закон
- 17. Пример. Составить закон распределения числа попаданий в
- 18. Упражнения.1. Составить закон распределения числа попаданий в
- 19. Числовые характеристикираспределения дискретных случайных величин
- 20. На практике нет необходимости характеризовать случайную величину
- 21. Определение. Математическим ожиданием М(Х) дискретной случайной величины
- 22. Свойства математического ожидания1. Постоянный множитель можно выносить
- 23. 4. Математическое ожидание любой линейной комбинации случайных
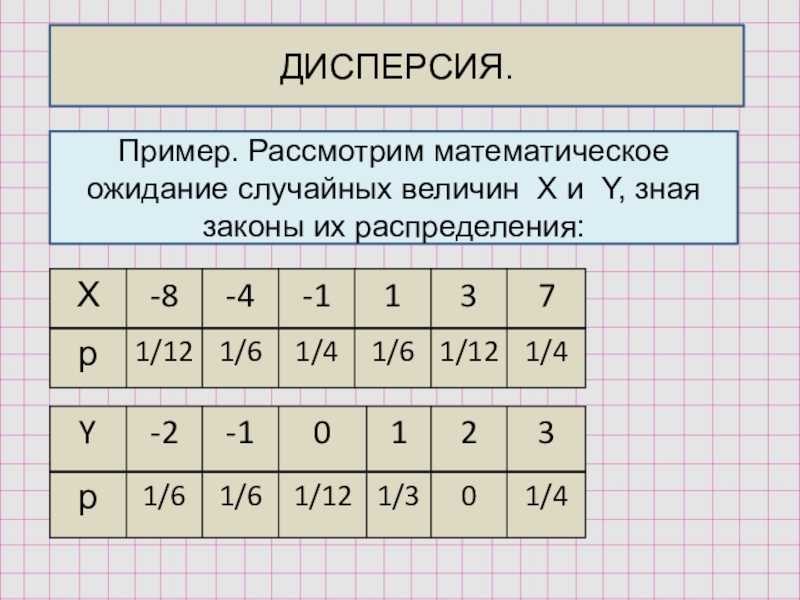
- 24. ДИСПЕРСИЯ.Пример. Рассмотрим математическое ожидание случайных величин X и Y, зная законы их распределения:
- 25. Основной числовой характеристикой степени рассеяния значений случайной
- 26. Свойства дисперсииДисперсия постоянной величины равна нулю: D
- 27. Для вычисления дисперсий более удобной является формула:D (X) = М (Х2) – (М (Х))2
- 28. Пример.Дискретная случайная величина распределена по закону:Найти D(X).
- 29. 1. Найти математическое ожидание случайной величины Х,
- 30. 3. Найти дисперсию случайной величины Х, если
- 31. Контрольные вопросыДать определение случайной величины.Какая случайная величина
Слайд 2Цель занятия:
Познакомиться с понятием дискретной случайной величины, научиться составлять её закон
Слайд 3Случайное событие, связанное с некоторым опытом, является качественной характеристикой опыта.
Количественной
Слайд 4Определение 1. Случайной называется величина, которая в результате опыта принимает с
Обозначения случайных величин:
X, Y, Z,.., а их значений соответственно: x, y, z, …
Слайд 5Пример 1. Игрок бросает монету – при выпадении герба он выигрывает
Пример 2. Эксперимент – одновременное бросание двух игральных кубиков, случайная величина – сумма выпавших очков, может принимать все целые значения от 2 до 12 в зависимости от выпавшей комбинации.
Слайд 6Пример 3. Эксперимент – n-кратное повторение опыта с бросанием монеты, случайная
Пример 4. Эксперимент – извлечение шара из урны, содержащей равное количество белых и черных шаров, с возвращением шара в урну после каждого извлечения. Случайная величина – количество извлечений до первого появления белого шара.
Эта случайная величина может принимать …
все целые положительные значения: 1, 2, 3, …, n, …
Слайд 7Пример 5. Эксперимент – случайный выбор точки из отрезка [0; 1].
любые значения от 0 до 1.
Пример 6. Эксперимент – наблюдение за временем безотказной работы некоторого устройства: от момента включения до первого выхода из строя. Случайная величина – время безотказной работы – может принимать …
все действительные числа от 0 до +∞.
Слайд 8Определение 2. Случайная величина называется дискретной, если множество ее значений конечно
х1, х2, …, хn или бесконечную последовательность х1, х2, …, хn, …
Вероятность того, что случайная величина Х примет значение х, обозначают
Р(х) = Р(Х = х).
Слайд 9Определение 3. Соответствие между возможными значениями х1, х2, …, хn случайной
Закон распределения случайной величины может быть представлен в виде таблицы
Слайд 10
События Х = х1, Х = х2, …, Х = хn
р1 + р2 + … + рn = 1.
х1
х1
Слайд 12Над случайными величинами устанавливаются операции сложения и умножения
1. Суммой двух случайных
2. Произведением двух случайных величин X и Y называется случайная величина, которая получается в результате перемножения всех значений случайной величины Х и всех значений случайной величины Y, соответствующие вероятности перемножаются.
Слайд 14Биномиальное распределение
Пусть случайная величина Х – число появлений события А в
Слайд 15Определение. Биномиальным распределением называется закон распределения случайной величины Х, имеющий вид:
Пример.
Слайд 16Пример. Монета бросается 5 раз, представим закон распределения ДСВ Х –
Слайд 17Пример. Составить закон распределения числа попаданий в цель при четырех выстрелах,
Слайд 18Упражнения.
1. Составить закон распределения числа попаданий в цель при шести выстрелах,
2. Вероятность того, что студент найдет в библиотеке нужную ему книгу, равна 0,3. Составить закон распределения числа библиотек, которые он посетит, если в городе четыре библиотеки.
Слайд 20На практике нет необходимости характеризовать случайную величину полностью. Обычно достаточно указать
Слайд 21Определение. Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений
М(Х) = х1р1 + х2р2 + … + хnрn= хiрi
Пример. Найти математическое ожидание случайной величины Х, зная ее закон распределения:
Слайд 22Свойства математического ожидания
1. Постоянный множитель можно выносить за знак математического ожидания:
2. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
М(X + Y) = M (X) + M (Y).
3. Математическое ожидание постоянной величины С равно самой этой величине: М (С) = С.
Слайд 234. Математическое ожидание любой линейной комбинации случайных величин равно линейной комбинации
М ( Сk Хk) = (Сk M (Хk)).
5. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
M (XY) = M (X) M(Y).
Слайд 24ДИСПЕРСИЯ.
Пример. Рассмотрим математическое ожидание случайных величин X и Y, зная законы
Слайд 25Основной числовой характеристикой степени рассеяния значений случайной величины Х относительно ее
Определение. Отклонением называется разность между случайной величиной Х и ее математическим ожиданием М (Х), т.е. Х – М (Х).
Определение. Дисперсией дискретной случайной величины Х называется математическое ожидание квадрата ее отклонения: D (X) = М (Х – М (Х))2.
Слайд 26Свойства дисперсии
Дисперсия постоянной величины равна нулю:
D (X) = 0.
2. Если
D (X + С) = D (X).
3. Если Х и Y– независимые случайные величины, то D (X + Y) = D (X) + D (Y).
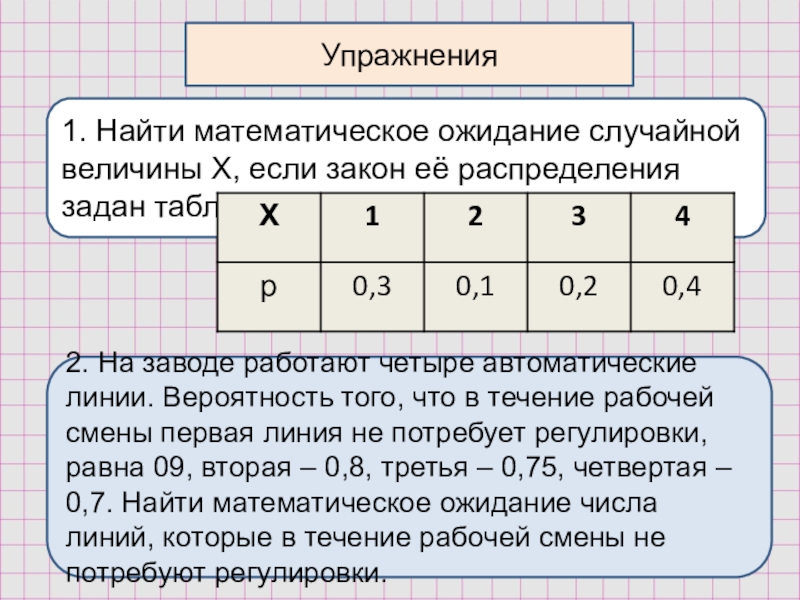
Слайд 291. Найти математическое ожидание случайной величины Х, если закон её распределения
Упражнения
2. На заводе работают четыре автоматические линии. Вероятность того, что в течение рабочей смены первая линия не потребует регулировки, равна 09, вторая – 0,8, третья – 0,75, четвертая – 0,7. Найти математическое ожидание числа линий, которые в течение рабочей смены не потребуют регулировки.
Слайд 303. Найти дисперсию случайной величины Х, если закон её распределения задан
4. Охотник стреляет по дичи до первого попадания, но успевает делать не более четырех выстрелов. Найти дисперсию числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7.
Слайд 31Контрольные вопросы
Дать определение случайной величины.
Какая случайная величина называется дискретной?
Какое соответствие называется
Какая случайная величина называется суммой двух случайных величин X и Y?
Какая случайная величина называется произведением двух случайных величин X и Y?
С какими числовыми характеристиками распределения дискретных случайных величин вы познакомились?
Что называется математическим ожиданием М(Х) дискретной случайной величины Х?
Перечислите свойства математического ожидания дискретной случайной величины Х.
Что называется дисперсией дискретной случайной величины Х?
Перечислите свойства дисперсии дискретной случайной величины Х.






![Дискретные случайные величины Пример 5. Эксперимент – случайный выбор точки из отрезка [0; 1]. Пример 5. Эксперимент – случайный выбор точки из отрезка [0; 1]. Случайная величина – координата точки. Эта](/img/thumbs/4eed9a462b2b4ae8bbd62b7bd83e0402-800x.jpg)