чисел из изображаемых их символов.
Примеры: двоичная (0,1), десятичная (0,1,2,3,4,5,6,7,8,9), римская (I,V,X,L,C,D,M).
Позиционная система счисления- значение цифры зависит от ее положения среди других цифр(римская).
Непозиционная система счисления – значение цифры не зависит от ее положения среди других.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Системы счисления для 9 класса
Содержание
- 1. Презентация Системы счисления для 9 класса
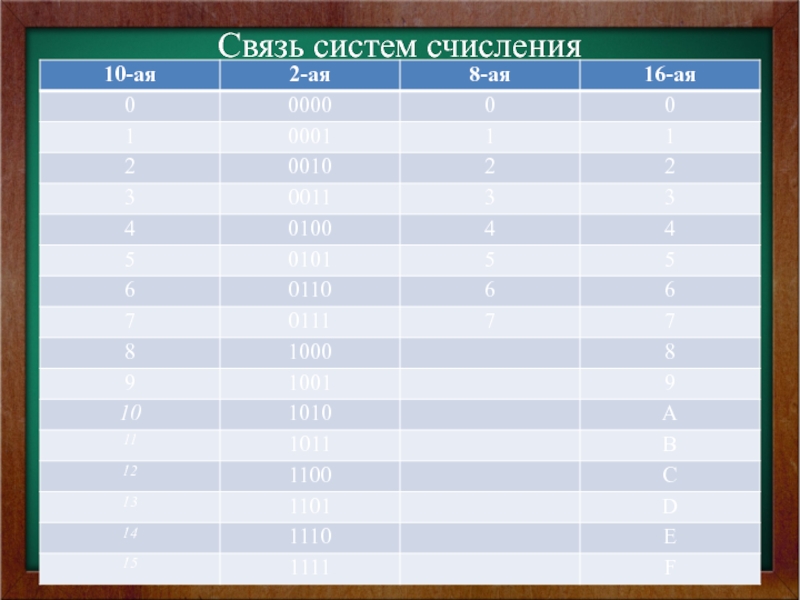
- 2. Связь систем счисления
- 3. Переход из любой системы счисления в десятичную:
- 4. Пример 1.1. 101101102 = =(1·27)+(0·26)+(1·25)+(1·24)+(0·23)++(1·22)+(1·21)+(0·20) =
- 5. Переход из десятичной системы счисления в любую
- 6. Пример 2.1.2710=110112
- 7. Пример 2.2. Остаток от деления записываем в
- 8. Пример 2.3. Остаток от деления записываем в
- 9. Переход из 2-ой в 16-ую делается условным разбиением числа на четверки. Пример 2.4. 1000.1111.1011.11112=8FBF16Пример 2.5. 0001.1000.1111.00102=18F216
Связь систем счисления
Слайд 3Переход из любой системы счисления в десятичную:
Для перевода в десятичную систему
счисления необходимо найти сумму произведений основания данной системы счисления на соответствующую степень разряда.
А - данное число, p-основание системы счисления числа А, a- цифры из числа А, m-разряды в целой части числа А, n-разряды в дробной части числа А.
А - данное число, p-основание системы счисления числа А, a- цифры из числа А, m-разряды в целой части числа А, n-разряды в дробной части числа А.
Слайд 4Пример 1.1. 101101102 = =(1·27)+(0·26)+(1·25)+(1·24)+(0·23)+
+(1·22)+(1·21)+(0·20) = 128+32+16+4+2 = 18210
Пример 1.2.
1637 = 1*72 + 6*71 + 3*70 = =49+42+3=9410
Пример 1.3. 234,68 = 2*82 +3*81 + 4*80 +6*8-1= 2*64+3*8+4+6*0,125= 128+24+4+0,75 =156,7510
Пример 1.4. 4E7F.3F116= 4*163 + 14*162 + 7*161 + 15*160 + 3*16-1 + 15*16-2 + 1*16-3= =16384 + 3584 + 112 + 15 + 0.1875 + 0.05859375 + 0.000244140625 = 20095.24633789062510
Пример 1.3. 234,68 = 2*82 +3*81 + 4*80 +6*8-1= 2*64+3*8+4+6*0,125= 128+24+4+0,75 =156,7510
Пример 1.4. 4E7F.3F116= 4*163 + 14*162 + 7*161 + 15*160 + 3*16-1 + 15*16-2 + 1*16-3= =16384 + 3584 + 112 + 15 + 0.1875 + 0.05859375 + 0.000244140625 = 20095.24633789062510
Слайд 5Переход из десятичной системы счисления в любую другую:
разделить число на основание
переводимой системы счисления;
найти остаток от деления целой части числа;
записать все остатки от деления в обратном порядке;
найти остаток от деления целой части числа;
записать все остатки от деления в обратном порядке;
Слайд 7Пример 2.2.
Остаток от деления записываем в обратном порядке. Получаем число
в 2-ой системе счисления: 1101010
106 = 11010102
Слайд 8Пример 2.3.
Остаток от деления записываем в обратном порядке. Получаем число
в 8-ой системе счисления: 0207
135 = 2078
Слайд 9Переход из 2-ой в 16-ую делается условным разбиением числа на четверки.
Пример
2.4. 1000.1111.1011.11112=8FBF16
Пример 2.5. 0001.1000.1111.00102=18F216
Пример 2.5. 0001.1000.1111.00102=18F216