- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Решение задач ЕГЭ №18
Содержание
- 1. Презентация по информатике Решение задач ЕГЭ №18
- 2. Выдержка из кодификатора элементов содержанияЗнания о:формах мышления
- 3. Формулы логики A. Свойства 0, 1 и отрицанияСвойства 0 и 1Свойства отрицания
- 4. Формулы логики Б. Дизъюнкция и конъюнкцияСочетательный законПереместительный законЗакон повторенияРаспределительный законПравила де Моргана
- 5. Формулы логикиВ. Импликация и эквивалентностьОпределение импликацииСвойства импликацииЭквивалентность
- 6. Вопросы методики подготовки обучающихся к выполнению задания 18 КИМ ГИА-11 по информатике и ИКТ
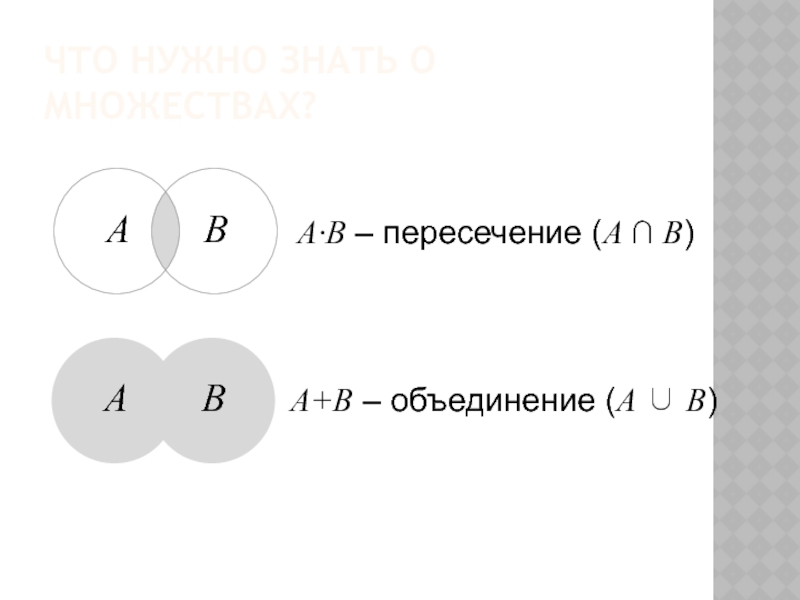
- 7. Что нужно знать о множествах?A(все натуральные)U –
- 8. Что нужно знать о множествах?A·B – пересечение (A B)A+B – объединение (A B)
- 9. Множества и логические функцииМножество задаётся логической функцией
- 10. Основные типы заданий №18
- 11. Решение заданий №18 с использованием таблиц истинности
- 12. Рекомендуемая схема №1 выполнения задания №18 КИМ ГИА-11
- 13. Решение заданий №18 с использованием битовых цепочек
- 14. 2. Построим битовую цепочку для данного выражения.
- 15. Обозначим через ДЕЛ(n, m) утверждение «натуральное число
- 16. Обозначим через ДЕЛ(n, m) утверждение «натуральное число
- 17. Обозначим через ДЕЛ(n, m) утверждение «натуральное число
- 18. Обозначим через ДЕЛ(n, m) утверждение «натуральное число
- 19. 6. А минимальное = 3Обозначим через ДЕЛ(n,
- 20. Решение заданий №18 с неравенствами
- 21. Рекомендуемая схема №2 выполнения задания №18
- 22. 1. Определим предельные значения X и Y
- 23. 2. Подставим найденные значения X и Y
- 24. 1. Определим предельные значения X и Y
- 25. 2. Подставим найденные значения X и Y
- 26. 1. Определим предельные значения X и Y
- 27. 3. Определим количество целых значений А, при
Слайд 2Выдержка из кодификатора элементов содержания
Знания о:
формах мышления (понятии, суждении, умозаключении);
основных логических
законах логики;
методах решения логических уравнений и систем логических уравнений;
базовых логических элементов компьютера (Сумматоре, триггере).
Умения
построить диаграммы Эйлера-Венна.
построить таблицы истинности для сложных высказываний.
строить и преобразовывать логические выражения.
анализировать схемы, построенные с использованием базовых логических элементов компьютера и строить для них таблицы истинности.
Слайд 4Формулы логики
Б. Дизъюнкция и конъюнкция
Сочетательный закон
Переместительный закон
Закон повторения
Распределительный закон
Правила де
Слайд 5Формулы логики
В. Импликация и эквивалентность
Определение импликации
Свойства импликации
Эквивалентность
Слайд 6Вопросы методики подготовки обучающихся к выполнению задания 18 КИМ ГИА-11 по
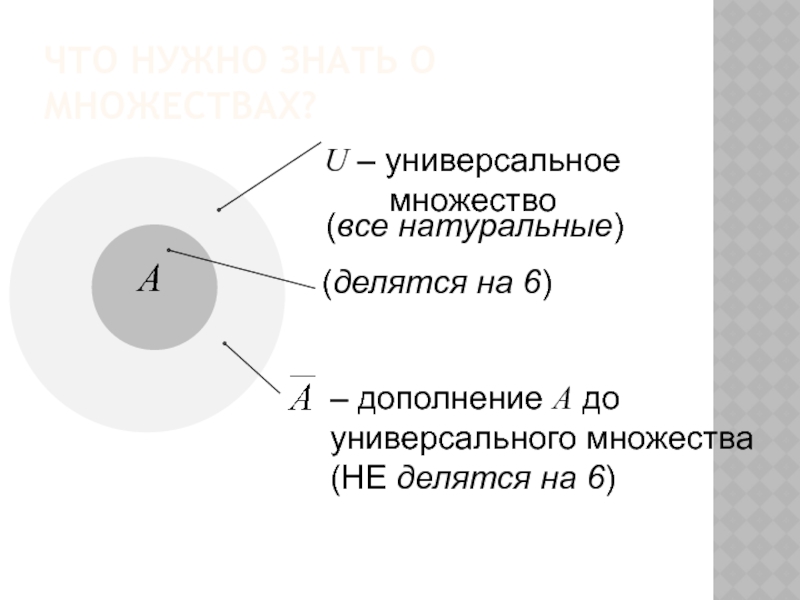
Слайд 7Что нужно знать о множествах?
A
(все натуральные)
U – универсальное
– дополнение A до универсального множества
(НЕ делятся на 6)
Слайд 9Множества и логические функции
Множество задаётся логической функцией
x A
x A+B
A(x) = 1
Слайд 142. Построим битовую цепочку для данного выражения. Нас интересуют ситуации, когда
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула
¬ДЕЛ(x, А) (ДЕЛ(x, 6) ¬ДЕЛ(x, 4))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Слайд 15Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка
¬ДЕЛ(x, А) (ДЕЛ(x, 6) ¬ДЕЛ(x, 4))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
6. А максимальное = 2 х 2 х 3 =12
Слайд 16Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка
¬ДЕЛ(x, А) (¬ДЕЛ(x, 21) ¬ ДЕЛ(x, 35))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
2. Построим битовую цепочку для данного выражения. Нас интересуют ситуации, когда достигается 0.
Слайд 17Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка
¬ДЕЛ(x, А) (¬ДЕЛ(x, 21) ¬ ДЕЛ(x, 35))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
6. А максимальное = 7
Слайд 18Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка
(ДЕЛ(x, 15) ¬ДЕЛ(x, 21)) (¬ДЕЛ(x, A) ¬ДЕЛ(x, 15))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
2. Построим битовую цепочку для данного выражения. Нас интересует ситуация, когда достигается 0.
Слайд 196. А минимальное = 3
Обозначим через ДЕЛ(n, m) утверждение «натуральное число
(ДЕЛ(x, 15) ¬ДЕЛ(x, 21)) (¬ДЕЛ(x, A) ¬ДЕЛ(x, 15))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Слайд 21Рекомендуемая схема №2
выполнения задания №18 КИМ ГИА-11
Основная идея: находим значения
«ненужные» значения. Затем подбираем значение А, при котором общее высказывание
становится правильным
Слайд 221. Определим предельные значения X и Y при которых выражение обращается
Укажите наименьшее целое значение А, при котором выражение
(x 7) ∨ (2x < y) ∨ (xy < A)
истинно для любых целых положительных значений x и y.
Слайд 23
2. Подставим найденные значения X и Y в высказывание, содержащее неизвестный
Высказывание (х y < A) должно быть истинным, поэтому А=73.
Укажите наименьшее целое значение А, при котором выражение
(x 7) ∨ (2x < y) ∨ (xy < A)
истинно для любых целых положительных значений x и y.
Слайд 241. Определим предельные значения X и Y при которых выражение обращается
Укажите наименьшее целое значение А, при котором выражение
(y + 3x < A) ∨ (2y +x > 50) ∨ (4y – x < 40)
истинно для любых целых положительных значений x и y.
x=50-30
x=20
Слайд 252. Подставим найденные значения X и Y в высказывание, содержащее неизвестный
Укажите наименьшее целое значение А, при котором выражение
(y + 3x < A) ∨ (2y +x > 50) ∨ (4y – x < 40)
истинно для любых целых положительных значений x и y.
Высказывание ( y+3x < A) должно быть истинным, поэтому А=76
Слайд 261. Определим предельные значения X и Y при которых выражение обращается
Сколько существует целых значений А, при которых формула
( (x > 6) ∧ (x⋅x ≤ A)) ∨ ((y⋅y ≥ A) ∧ (y < 5))
тождественно ложна (то есть принимает значение 0 при любых целых неотрицательных значениях переменных x и y)?
2. Подставим найденные значения X и Y в высказывание, содержащее неизвестный параметр А и определим наибольшее значение, при котором выражение ложно.
Слайд 273. Определим количество целых значений А, при которых выражение ложно:
Сколько
( (x > 6) ∧ (x⋅x ≤ A)) ∨ ((y⋅y ≥ A) ∧ (y < 5))
тождественно ложна (то есть принимает значение 0 при любых целых неотрицательных значениях переменных x и y)?
Количество значений