- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике по теме Определение количества информации
Содержание
- 1. Презентация по информатике по теме Определение количества информации
- 2. ИНФОРМАЦИЯ Понятие «информация» является общенаучным, используется в информатике, физике, кибернетике, биологии и др. науках
- 3. ИЗМЕРЕНИЕ ИНФОРМАЦИИ Вероятностный подходАлфавитный подход ИНФОРМАЦИЯ Подходы
- 4. ИЗМЕРЕНИЕ ИНФОРМАЦИИ: вероятностный подход Информация для человека
- 5. ИЗМЕРЕНИЕ ИНФОРМАЦИИИнформация, которую получает человек, приводит к
- 6. ИЗМЕРЕНИЕ ИНФОРМАЦИИ Сколько равновероятных событий может произойти
- 7. ИЗМЕРЕНИЕ ИНФОРМАЦИИЕдиницей количества информации является 1 бит
- 8. ИЗМЕРЕНИЕ ИНФОРМАЦИИ 1 байт = 23 бит
- 9. ИЗМЕРЕНИЕ ИНФОРМАЦИИКакова связь между количеством возможных событий
- 10. ИЗМЕРЕНИЕ ИНФОРМАЦИИ: содержательный (вероятностный) подходДля равновероятных событий:N
- 11. РЕШЕНИЕ ЗАДАЧКакое количество информации несет в себе
- 12. РЕШЕНИЕ ЗАДАЧКакое количество информации получит второй игрок
- 13. РЕШЕНИЕ ЗАДАЧСообщение о том, что ваш друг
- 14. Пример:После экзамена по информатике, который сдавали ваши
- 15. РешениеДля учащегося A все четыре оценки (события)
- 16. ЗадачаВ непрозрачном мешочке хранятся 10 белых, 20
- 17. РешениеТак как количество шариков различных цветов неодинаково,
- 18. ЗадачаКакое количество вопросов достаточно задать вашему собеседнику, чтобы наверняка определить месяц, в котором он родился?
- 19. РешениеБудем рассматривать 12 месяцев как 12 возможных
- 20. РешениеПравильно задавать «двоичные» вопросы, т.е. вопросы, на
- 21. РешениеПо формуле получаем: I = log212
- 22. Пример1 Сколько бит информации несет сообщение о том, из колоды в 32 карты достали даму пик?
- 23. Решение N = 2i N=32 — число
- 24. Пример 2Сколько информации несет сообщение о том,
- 25. Пример 3Сколько информации несет сообщение о том,
- 26. Пример4Проводится две лотереи: «4 из 32» и
- 27. РешениеВыбор 1-го шара производится из 32 шаров
- 28. РЕШЕНИЕ ЗАДАЧ1. В рулетке общее количество лунок
- 29. РЕШЕНИЕ ЗАДАЧ5. При угадывании целого числа в
- 30. РЕШЕНИЕ ЗАДАЧКакое количество информации о цвете вынутого
- 31. РЕШЕНИЕ ЗАДАЧ7. Какое количество информации о цвете
- 32. Позволяет определить количество информации в тексте, отвлекаясь
- 33. Количество информации несет в тексте каждый символ
- 34. Для русского алфавита (без буквы ё):Мощность алфавита
- 35. ИЗМЕРЕНИЕ ИНФОРМАЦИИ: алфавитный подходАлфавит из 256 символов
- 36. ЗадачаКакова минимальная мощность алфавита, с помощью которого
- 37. РешениеПредположим, что используемый алфавит состоит всего из
- 38. Полученный выводможно проиллюстрировать следующим образным примером. Представьте
- 39. Минимальная мощность алфавитаМинимальная мощность алфавита, пригодного для
- 40. ЗадачаДва текста содержат одинаковое количество символов Первый
- 41. РешениеВ равновероятном приближении информационный объем текста равен
- 42. ЗадачаОбъем сообщения, содержащего 1024 символов, составил 1/512
- 43. РешениеПереведем информационный объем сообщения из мегабайтов в
- 44. ЗадачаКакова мощность алфавита, с помощью которого записано
- 45. Решение1. Переведём информационный объем сообщения в биты:
- 46. 1. Книга, набранная с помощью компьютера, содержит
- 47. РЕШЕНИЕ ЗАДАЧ5. Объем сообщения, содержащего 2048 символов,
- 48. 9. Для записи сообщения использовался 64-х символьный
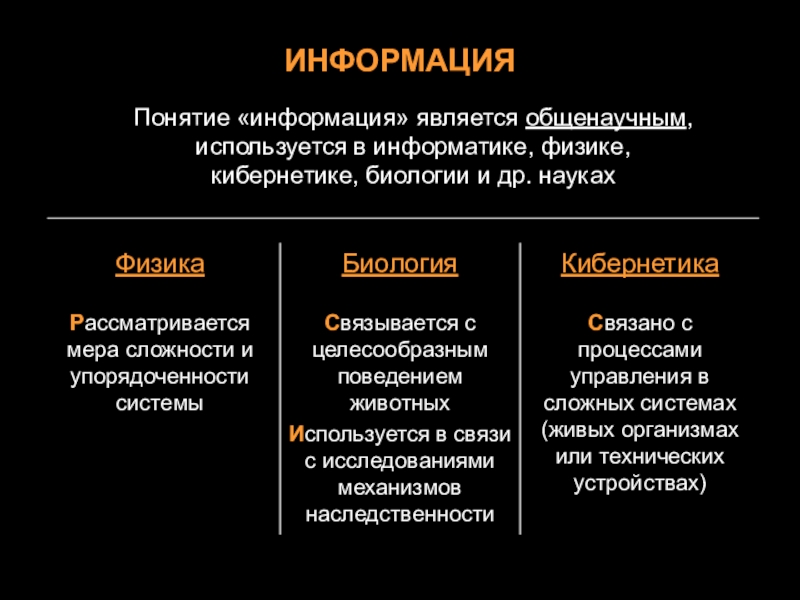
Слайд 2ИНФОРМАЦИЯ
Понятие «информация» является общенаучным, используется в информатике, физике,
кибернетике, биологии
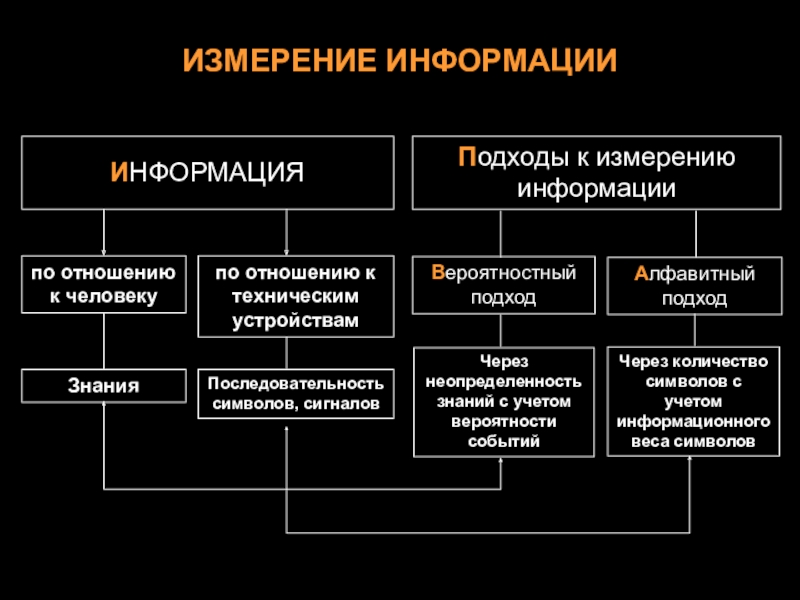
Слайд 3ИЗМЕРЕНИЕ ИНФОРМАЦИИ
Вероятностный подход
Алфавитный подход
ИНФОРМАЦИЯ
Подходы к измерению информации
по отношению к человеку
по
Знания
Последовательность символов, сигналов
Через неопределенность знаний с учетом вероятности событий
Через количество символов с учетом информационного веса символов
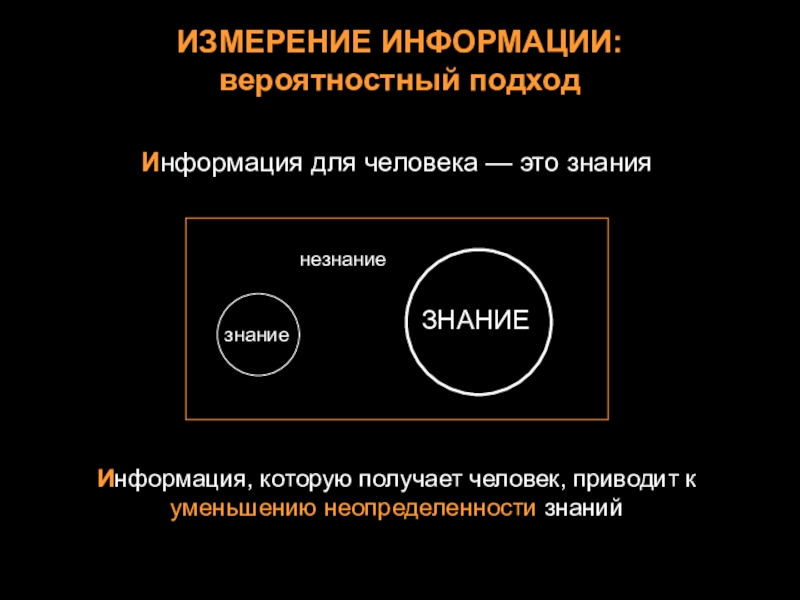
Слайд 4ИЗМЕРЕНИЕ ИНФОРМАЦИИ:
вероятностный подход
Информация для человека — это знания
знание
ЗНАНИЕ
Информация, которую получает
незнание
Слайд 5ИЗМЕРЕНИЕ ИНФОРМАЦИИ
Информация, которую получает человек, приводит к уменьшению неопределенности знаний
Сообщение о
Возможные события.
Они равновероятны
Произошедшее событие
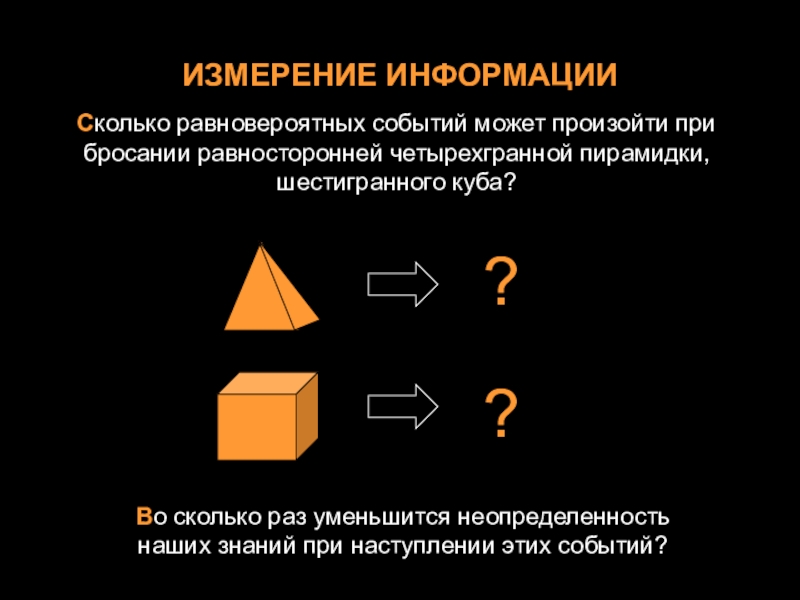
Слайд 6ИЗМЕРЕНИЕ ИНФОРМАЦИИ
Сколько равновероятных событий может произойти при бросании равносторонней четырехгранной
?
?
Во сколько раз уменьшится неопределенность
наших знаний при наступлении этих событий?
Слайд 7ИЗМЕРЕНИЕ ИНФОРМАЦИИ
Единицей количества информации является 1 бит – величина, уменьшающая неопределенность
Какое количество информации получено
при наступлении события?
Слайд 8ИЗМЕРЕНИЕ ИНФОРМАЦИИ
1 байт = 23 бит = 8 бит
1 Кбайт =
1 Тбайт=210 Гбайт = 1024 Гбайт
1 PB (петабайт) = 210 Tбайт
1 EB (эксабайт) = 210 Пбайт
1 ZB (зеттабайт) = 210 Эбайт
1 YB (йоттабайт) = 210 Збайт
Слайд 9ИЗМЕРЕНИЕ ИНФОРМАЦИИ
Какова связь между количеством возможных событий и количеством полученной информации?
1
Слайд 10ИЗМЕРЕНИЕ ИНФОРМАЦИИ:
содержательный (вероятностный) подход
Для равновероятных событий:
N = 2I
где N – количество
Для событий с различными вероятностями (формула Шеннона):
где N – количество возможных событий,
I – количество информации,
pi – вероятность i-го события
Слайд 11РЕШЕНИЕ ЗАДАЧ
Какое количество информации несет в себе сообщение
о том, что нужная
N = 2I
8 = 2I
Ответ: 3 бита
Слайд 12РЕШЕНИЕ ЗАДАЧ
Какое количество информации получит второй игрок при игре в крестики-нолики
N = 2I
64 = 2I
Ответ: 6 бит
Слайд 13РЕШЕНИЕ ЗАДАЧ
Сообщение о том, что ваш друг живет на десятом этаже
N = 2I
N = 24
Ответ: 16
Слайд 14Пример:
После экзамена по информатике, который сдавали ваши друзья, объявляются оценки («2»,
Какое количество информации будет нести сообщение об оценке учащегося A, который выучил лишь половину билетов,
и сообщение об оценке учащегося B, который выучил все билеты.
Слайд 15Решение
Для учащегося A все четыре оценки (события) равновероятны тогда количество информации,
I = log24 = 2 бит
Для учащегося B наиболее вероятной оценкой является «5» (p1 = 1/2), вероятность оценки «4» в два раза меньше (p2 = 1/4), а вероятности оценок «2» и «3» еще в два раза меньше (p3 = p4 = 1/8).
Так как события неравновероятны, воспользуемся для подсчета количества информации в сообщении формулой:
I = -(1/2∙log21/2 + 1/4∙log21/4 + 1/8∙log21/8 + 1/8∙log21/8) бит = 1,75 бит
Вычисления показали, что при равновероятных событиях мы получаем большее количество информации, чем при неравновероятных событиях.
Слайд 16Задача
В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и
Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика.
Слайд 17Решение
Так как количество шариков различных цветов неодинаково, то зрительные сообщения о
Рб = 0,1; Рк = 0,2; Рс = 0,3; Рз = 0,4
События неравновероятны, поэтому для определения количества информации, содержащимся в сообщении о цвете шарика, воспользуемся формулой:
I = -(0,1∙log2 0,1+ 0,2∙log2 0,2 + 0,3∙log2 0,3 + 0,4∙log2 0,4) бит = 1,85 бит
Слайд 18Задача
Какое количество вопросов достаточно задать вашему собеседнику, чтобы наверняка определить месяц,
Слайд 19Решение
Будем рассматривать 12 месяцев как 12 возможных событий. Если спрашивать о
Слайд 20Решение
Правильно задавать «двоичные» вопросы, т.е. вопросы, на которые можно ответить только
Правильная стратегия состоит в том, что вопросы нужно задавать так, чтобы количество возможных вариантов каждый раз уменьшалось вдвое. Тогда количество возможных событий в каждом из полученных подмножеств будет одинаково и их отгадывание равновероятно. В этом случае на каждом шаге ответ («Да» или «Нет») будет нести максимальное количество информации (1 бит).
Слайд 21Решение
По формуле получаем:
I = log212 ≈ 3,6 бит
Количество
Округляем до большего целого числа и получаем ответ: при правильной стратегии необходимо задать не более 4 вопросов.
Слайд 22Пример1
Сколько бит информации несет сообщение о том, из колоды в 32
Слайд 23Решение
N = 2i
N=32 — число карт в колоде.
i — количество информации
2i=25, т.к. 32=25, то, i = 5бит.
Слайд 24Пример 2
Сколько информации несет сообщение о том, что из колоды карт
Решение.
N = 2i
N = 2
2=2i I =1
Ответ: (1 бит, так как красных и черных карт одинаковое количество).
Слайд 25Пример 3
Сколько информации несет сообщение о том, что из колоды карт
Решение.
N = 2i
N = 4
22=2i I =2
Ответ: (2 бита, так как всего в колоде 4 масти и количество карт в них равные).
Слайд 26Пример4
Проводится две лотереи: «4 из 32» и «5 из 64». Сообщение
Слайд 27Решение
Выбор 1-го шара производится из 32 шаров в барабане. 2i =
2-й шар будет выбираться уже из 31 номера, 2i = 31, i = 4,95420 бит.
3-й — из 30 номеров, 2i = 30; i = 4,90689 бит
4-й — из 29, 2i = 29; i = 4,85798 бит.
Cумма S=5 + 4,95420 + 4,90689 + 4,85798 = 19,71907 бит.
Ответ: второе сообщение несет больше информации, чем первое
Слайд 28РЕШЕНИЕ ЗАДАЧ
1. В рулетке общее количество лунок равно 128. Какое количество
2. Происходит выбор одной карты из колоды в 32 карты.
Какое количество информации мы получим при выборе одной карты?
3. Сообщение о том, что Пети живет во втором подъезде, несет 3 бита информации. Сколько подъездов в доме?
4. В школьной библиотеке 16 стеллажей с книгами. На каждом стеллаже 8 полок. Библиотекарь сообщил Пете, что нужная ему книга находится на пятом стеллаже на третьей сверху полке. Какое количество информации передал библиотекарь Пете?
Слайд 29РЕШЕНИЕ ЗАДАЧ
5. При угадывании целого числа в диапазоне от 1 до
6. При угадывании целого числа в некотором диапазоне было получено 6 бит информации. Сколько чисел содержит этот диапазон?
7. Какое количество информации о цвете вынутого шарика будет получено, если в непрозрачном пакете хранятся:
25 белых, 25 красных, 25 синих и 25 зеленых шариков?
8. Какое количество вопросов достаточно задать вашему собеседнику, чтобы точно определить день и месяц его рождения?
Слайд 30РЕШЕНИЕ ЗАДАЧ
Какое количество информации о цвете вынутого шарика будет получено, если
Pбел. = 10/100 = 0,1
Pкрасн. = 20/100 = 0,2
Pсин. = 30/100 = 0,3
Pзел. = 40/100 = 0,4
I = – (0,1∙log20,1 + 0,2∙log20,2 + 0,3∙log20,3 + 0,4∙log20,4) ≈ 1,85 бита
Ответ: 1,85 бита
Слайд 31РЕШЕНИЕ ЗАДАЧ
7. Какое количество информации о цвете вынутого шарика будет получено,
8. Заполните пропуски числами:
5 Кбайт = __ байт = __ бит
__ Кбайт = __ байт = 12288 бит
__ Кбайт = __ байт = 213 бит
__ Гбайт = 1536 Мбайт = __ Кбайт
512 Кбайт = 2? байт = 2? бит
Слайд 32Позволяет определить количество информации в тексте, отвлекаясь от содержания информации, воспринимая
Алфавит – множество символов, используемых для записи текста. Мощность алфавита – полное количество символов в алфавите.
ИЗМЕРЕНИЕ ИНФОРМАЦИИ:
алфавитный подход
Слайд 33Количество информации несет в тексте каждый символ (i), вычисляется из уравнения
2i = N,
где N — мощность алфавита.
i -информационный вес символа.
Отсюда следует, что:
Количество информации во всем тексте (I), состоящем из K символов, равно произведению информационного веса символа на К: I = i x К. Эту величину можно назвать информационным объемом текста.
Слайд 34Для русского алфавита (без буквы ё):
Мощность алфавита (количество равновероятных событий N)
тогда количество информации I, которое несет каждый символ, вычисляется по формуле:
ИЗМЕРЕНИЕ ИНФОРМАЦИИ:
алфавитный подход
32 = 2I
и равно 5 бит.
Какое количество информации несет один символ алфавита мощностью 2, 4, 8, 16, 256 символов?
Слайд 35ИЗМЕРЕНИЕ ИНФОРМАЦИИ:
алфавитный подход
Алфавит из 256 символов используется
для представления текстов в
Пусть К – количество символов в тексте,
i – информационный «вес» одного символа.
Тогда при алфавитном подходе размер информации, содержащейся в тексте I, вычисляется по формуле:
I = К · i
Слайд 36Задача
Какова минимальная мощность алфавита, с помощью которого можно записывать (кодировать) информацию?
«Докажите, что исходя из алфавитного подхода, сообщение любой длины, использующее односимвольный алфавит, содержит нулевую информацию».
Слайд 37Решение
Предположим, что используемый алфавит состоит всего из одного символа, например «1».
Информационный вес символа в таком алфавите находим из уравнения:
2i =1, 1 = 2°, то 2i = 2°, i=0 бит.
Слайд 38Полученный вывод
можно проиллюстрировать следующим образным примером. Представьте себе толстую книгу в
Слайд 39Минимальная мощность алфавита
Минимальная мощность алфавита, пригодного для передачи информации, равна 2.
Байт вводится как информационный вес символа из алфавита мощностью 256.
Слайд 40Задача
Два текста содержат одинаковое количество символов Первый текст составлен в алфавите
Слайд 41Решение
В равновероятном приближении информационный объем текста равен произведению числа символов на
1= K·i.
Поскольку оба текста имеют одинаковое число символов (К), то различие информационных объемов определяется только разницей в информативности символов алфавита (i). Найдем i1, для первого алфавита и i2 для второго алфавита: 2^i1 = 32, отсюда i1, = 5 бит;
: 2^i2 = 64, отсюда i2= 6 бит. Следовательно, информационные объемы первого и второго текстов будут равны:
I1= К·5 бит, I2=К·6 бит.
Отсюда следует, что количество информации во втором тексте , больше, чем в первом в 6/5, или в 1,2 раза.
Слайд 42Задача
Объем сообщения, содержащего 1024 символов, составил 1/512 часть Мбайта. Каков размер
Слайд 43Решение
Переведем информационный объем сообщения из мегабайтов в биты. Для этого данную
I=(1/512)· 1024· 1024·8 = 16 384 бит.
-Поскольку такой объем информации несут 1024 символа (К), на один символ приходится:
i= I/К = 16384/1024 = 16 бит.
Отсюда следует, что размер (мощность) использованного алфавита равен 2^16 = 65 536 символов.
Слайд 44Задача
Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов,
Слайд 45Решение
1. Переведём информационный объем сообщения в биты:
I = 10
2. Определить количество бит, приходящееся на один символ:
10 240 бит : 2 048 = 5 бит
3. По формуле определим количество символов в алфавите:
N = 2I = 25 = 32
Слайд 461. Книга, набранная с помощью компьютера, содержит 150 страниц. На каждой
2. Алфавит племени Мульти состоит из 8 букв. Какое количество информации несет одна буква этого алфавита?
3. Сообщение, записанное буквами из 64-х символьного алфавита, содержит 20 символов. Какой объем информации оно несет?
4. Информационное сообщение объемом 1,5 Кбайта содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого записано это сообщение?
РЕШЕНИЕ ЗАДАЧ
Слайд 47РЕШЕНИЕ ЗАДАЧ
5. Объем сообщения, содержащего 2048 символов, составил 1/512 часть Мбайта.
6. Сколько символов составляет сообщение, записанное с помощью 16-ти символьного алфавита, если объем его составил 1/16 часть Мбайта?
7. Сколько килобайтов составит сообщение из 384 символов 16-ти символьного алфавита?
8. Сообщение занимает 3 страницы по 25 строк. В каждой строке записано по 60 символов. Сколько символов в этом алфавите, если все сообщение содержит 1125 байт?
Слайд 489. Для записи сообщения использовался 64-х символьный алфавит. Каждая страница содержит
10. Сообщение занимает 2 страницы и содержит 1/16 Кбайт информации. На каждой странице записано 256 символов. Какова мощность алфавита?
11. Пользователь компьютера, хорошо владеющий навыками ввода информации с клавиатуры, может вводить в минуту 100 знаков. Мощность алфавита, используемого в компьютере, равна 256. Какое количество информации в байтах может ввести пользователь за 1 минуту.
12. Скорость чтения ученика 10 класса составляет приблизительно 250 символов в минуту. Приняв мощность используемого алфавита за 64, определите, какой объем информации в килобайтах получит ученик, если он будет непрерывно читать в течение 40 минут.