Информатика.
8 класс
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Основы логики (8 класс)
Содержание
- 1. Презентация по информатике Основы логики (8 класс)
- 2. Логика в информатикеЛогика – наука о формах
- 3. Высказывание по форме является повествовательным предложением. Высказывание
- 4. Высказывания. Задачиа) «сумма внутренних углов треугольника равна
- 5. ВысказыванияИз простых высказываний строятся составные высказывания. Например, «2*2=4 и 2
- 6. ВысказыванияА=«Два умножить на два равно четыре»В=«Два умножить
- 7. Базовые логические операцииЛогическое отрицание (Инверсия)Логическое умножение (Конъюнкция)Логическое сложение (Дизъюнкция)
- 8. Логические операции. ИнверсияЛогическое отрицание (инверсия) делает истинное
- 9. Логические операции. ДизъюнкцияСоставное высказывание, образованное в результате
- 10. Логические операции. КонъюнкцияСоставное высказывание, образованное в результате
- 11. Логические выраженияКаждое составное высказывание можно выразить в
- 12. Логические выраженияОпределен следующий порядок выполнения логических операций:
- 13. Таблицы истинностиДля каждого составного высказывания (логического выражения)
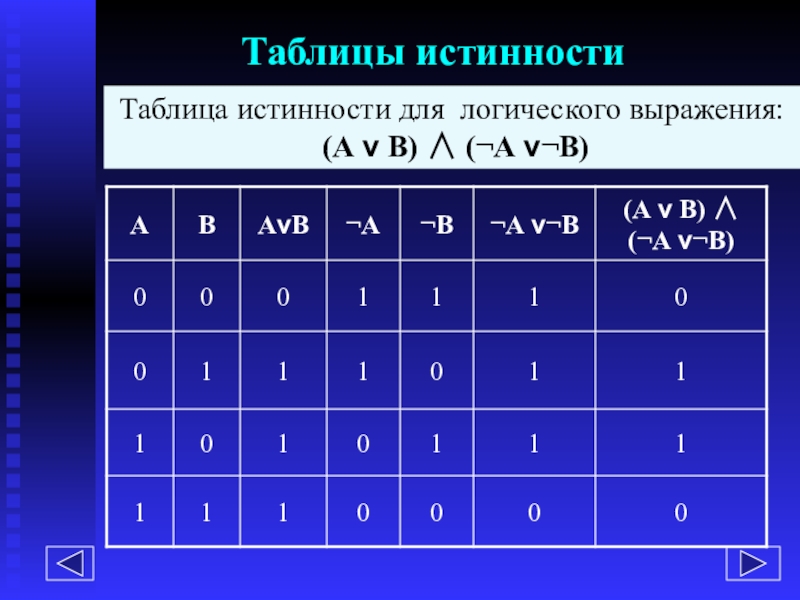
- 14. Таблицы истинностиТаблица истинности для логического выражения: (А v В) ∧ (¬А v¬В)
- 15. Логические законы и тождестваЛогического сложенияА v 0
- 16. Логические законы и тождестваЗаконы 1) А=А (Закон
- 17. 7. (АvB)vC=Av(BvC) (Ассоциативность сложения) 8. (A∧B)∧C=A∧(B∧C) (Ассоциативность
Логика в информатикеЛогика – наука о формах и способах мышления. Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть истинно или ложно.«2*2=4», «Москва
Слайд 1Презентация по теме «ОСНОВЫ ЛОГИКИ»
Рогачёва Ирина Викторовна,
учитель информатики
МБОУ «Гимназия № 5»
г. Рязань
Слайд 2Логика в информатике
Логика – наука о формах и способах мышления.
Высказывание
– это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть истинно или ложно.
«2*2=4», «Москва – столица России», «Луна – спутник Земли» являются истинными,
«Киев – столица Белоруссии», «Юпитер – спутник Марса» - ложными.
Слайд 3Высказывание по форме является повествовательным предложением.
Высказывание не может быть выражено
повелительным или вопросительным предложением, так как оценка их истинности или ложности невозможна.
Логика в информатике. Высказывания
Слайд 4Высказывания. Задачи
а) «сумма внутренних углов треугольника равна
двум прямым углам»
б) «верно ли, что π=3,1415926…?»
в) «44>88»
г) «математическое доказательство»
д) «Х+5=45»
е) «Любой ромб является параллелограммом»
ж) «Квадрат любого четного числа делится на 4»
б) «верно ли, что π=3,1415926…?»
в) «44>88»
г) «математическое доказательство»
д) «Х+5=45»
е) «Любой ромб является параллелограммом»
ж) «Квадрат любого четного числа делится на 4»
Какие из перечисленных ниже предложений являются высказываниями и каково их значение?
Слайд 5Высказывания
Из простых высказываний строятся составные высказывания.
Например, «2*2=4 и 2
составное высказывание, которое состоит из двух простых, соединенных логической операцией «и».
Слайд 6Высказывания
А=«Два умножить на два равно четыре»
В=«Два умножить на два равно семь»
Истинному
высказыванию ставят в соответствие 1, ложному – значение 0.
А=1 В=0
А=1 В=0
Поскольку для применения логических операций имеет значение лишь истинность или ложность высказываний, а не их содержание, то можно использовать алгебраический подход, заменив высказывания логическими переменными, обычно обозначаемыми латинскими буквами.
Слайд 7Базовые логические операции
Логическое отрицание (Инверсия)
Логическое умножение (Конъюнкция)
Логическое сложение (Дизъюнкция)
Слайд 8Логические операции. Инверсия
Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот,
ложное – истинным.
Таблица истинности операции логического отрицания:
Обозначение:
Ā, ¬А, НЕ А, NOT А.
А=«Мы любим математику»
¬А =Мы не любим математику»
Для каждого логического выражения можно построить таблицу, в которой для каждого набора значений простых логических переменных приведены значения этого выражения. Такая таблица называется таблицей истинности логического выражения.
Слайд 9Логические операции. Дизъюнкция
Составное высказывание, образованное в результате логического сложения (дизъюнкции) истинно
тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
Таблица истинности операции логического сложения
Обозначение:
АvВ, А+В, А|В, А or В, А ИЛИ В
А=«Я люблю математику»
В=«Я люблю физику»
«Я люблю математику ИЛИ физику»
Слайд 10Логические операции. Конъюнкция
Составное высказывание, образованное в результате логического умножения (конъюнкции) истинно
тогда и только тогда, когда истинны все входящие в него простые высказывания.
Таблица истинности операции логического умножения:
Обозначение:
А∧В, А&В, А⋅В, А И В,
А AND В.
А=«Я люблю математику»
В=«Я люблю физику»
«Я люблю математику И физику»
Слайд 11Логические выражения
Каждое составное высказывание можно выразить в виде формулы (логического выражения),
в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Запишем в форме логического выражения составное высказывание:
«(2*2=5 или 2*2=4)и(2*2≠5 или 2*2 ≠4)»
Оно содержит два простых высказывания:
А=«2*2=5» - ложь (А=0) и В=«2*2=4» - истина (В=1)
Тогда составное высказывание можно записать в виде:
«(А или В) и (¬А или ¬В)»
Что необходимо знать для выполнения логических операций?
Слайд 12Логические выражения
Определен следующий порядок выполнения логических операций:
1. Операции в скобках
2. Инверсия
3.
Конъюнкция
4. Дизъюнкция
Определим истинность логического выражения:
«(2*2=5 или 2*2=4)и(2*2≠5 или 2*2 ≠4)»
(А v В) ∧ (¬А v¬В)
(А v В) ∧ (¬А v¬В)=(0 v 1) ∧ (1 v 0)=1 ∧ 1=1
Слайд 13Таблицы истинности
Для каждого составного высказывания (логического выражения) можно построить таблицу истинности,
которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний (логических переменных).
Правила построения таблиц истинности:
1. Количество строк в таблице должно быть равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение.
Если количество переменных n, то количество строк – 2n
2. Количество столбцов равно количеству логических переменных плюс количество логических операций.
Построим таблицу истинности для логического выражения: (А v В) ∧ (¬А v ¬В)
Слайд 15Логические законы и тождества
Логического сложения
А v 0 = А
А v
1 = 1
А v А = А
А v¬А = 1
А v А = А
А v¬А = 1
Тождества
Логического умножения
А ∧ 0 = 0
2) А ∧ 1 = А
3) А ∧ А = А
4) А ∧¬А = 0
Слайд 16Логические законы и тождества
Законы
1) А=А (Закон тождества)
2) ¬(¬А)=А (Закон
двойного отрицания)
3) А∧( A∨B)=А (Закон поглощения)
4) А∨(A∧B)=А (Закон поглощения)
5) АvВ=BvA (Закон коммутативности сложения) 6) A∧B=B∧A (Закон коммутативности умножения)
3) А∧( A∨B)=А (Закон поглощения)
4) А∨(A∧B)=А (Закон поглощения)
5) АvВ=BvA (Закон коммутативности сложения) 6) A∧B=B∧A (Закон коммутативности умножения)
Слайд 177. (АvB)vC=Av(BvC) (Ассоциативность сложения) 8. (A∧B)∧C=A∧(B∧C) (Ассоциативность умножения) 9. A∧(BvC)=(A∧B)v(A∧C) (Дистрибутивность умножения относительно
сложения)
10. Av(B∧C)=(AvB)∧(AvC) (Дистрибутивность сложения относительно умножения)
11. ¬(AvB)= ¬A∧¬B
¬(A∧B)= ¬Av¬B
Законы
Законы де Моргана
Логические законы и тождества
