- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Сжатие двоичного кода (10 класс, профильный уровень)
Содержание
- 1. Презентация по информатике на тему Сжатие двоичного кода (10 класс, профильный уровень)
- 2. Любая информация в компьютере представляется в форме
- 3. Для сокращения объема данных выполняется их сжатие.Сжатие
- 4. При упаковке данных в файловые архивы производится
- 5. Например:Если сжатию подвергается текст, то после распаковки
- 6. Сжатие с частичной потерей информацииПроизводится при сжатии кода изображения (графики, видео) и звука.
- 7. Сжатие кода графики.Объем кода можно сократить за
- 8. Сжатие кода видео.Быстро меняющиеся фрагменты фильма можно кодировать менее подробно, чем статические кадры.
- 9. Сжатие кода звука.Поддается труднее всего.При хорошем качестве
- 10. Сжатие без потери информацииПервый подход: использование неравномерного кода.Второй подход: выявление повторяющихся фрагментов кода.
- 11. Использование неравномерного кода.Символы с меньшим информационным весом,
- 12. Одним из простейших, но весьма эффективных способов построения двоичного неравномерно кода, является алгоритм Дэвида Хаффмана
- 13. Алгоритм Хаффмана -Адаптивный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью.
- 14. Таблица ХаффманаВ этой таблице буквы расположены в
- 15. Префиксные кодыЧтобы понять, как строятся префиксные коды,
- 16. Префиксные кодыПостроим граф этого кода.Из начальной вершины
- 17. Префиксные кодыЕсли при этом какая-то последовательность оказывается
- 18. Слайд 18
- 19. Коэффициентом сжатия называют отношение длины кода в
- 20. Графическое изображение дерева Хаффмана, соответствующего табл. 1.8
- 21. Слайд 21
- 22. Пример: Предположим, что необходимо выполнить сжатие текстового
- 23. 1. Составляем таблицу частот, то есть, подсчитываем
- 24. 2. Сортируем значения в таблице по весам, в порядке спадания:
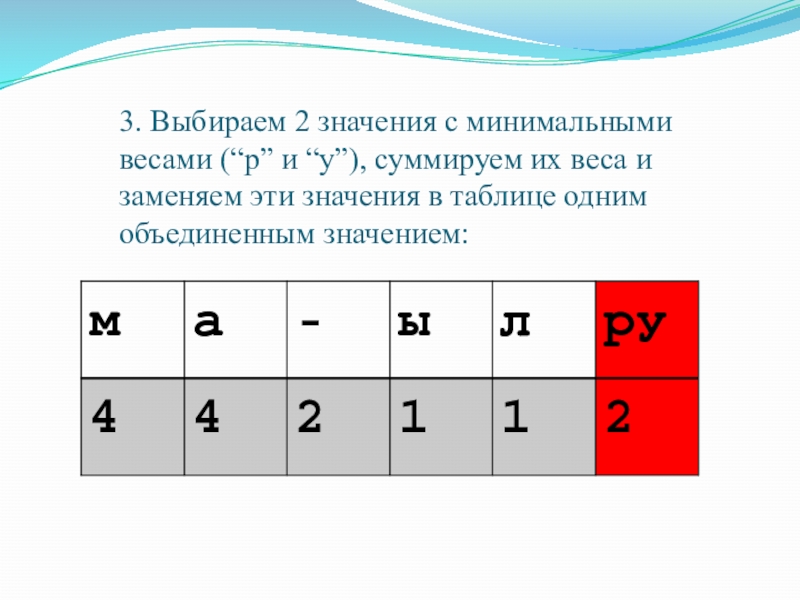
- 25. 3. Выбираем 2 значения с минимальными весами
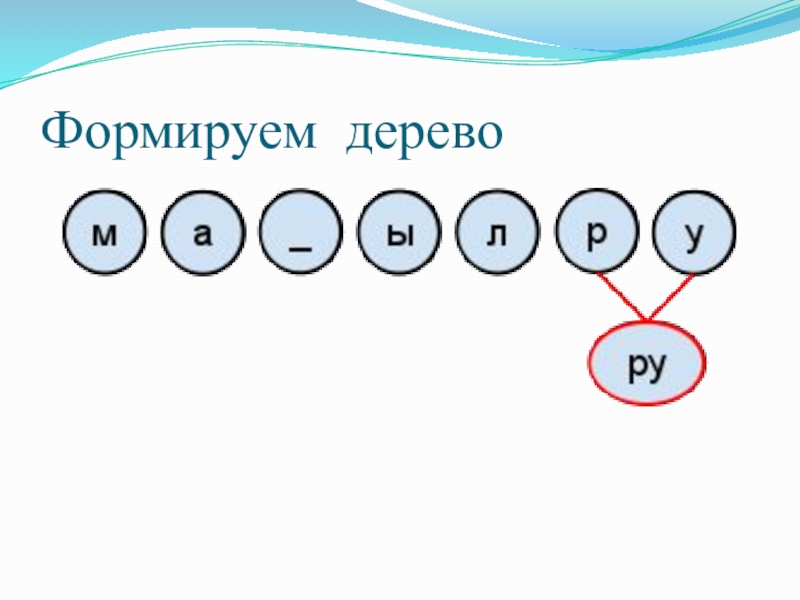
- 26. Формируем дерево
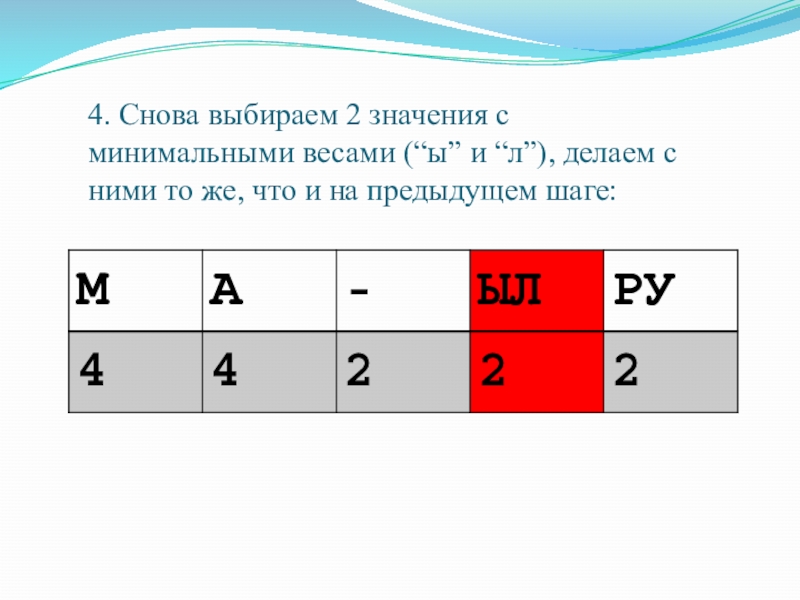
- 27. 4. Снова выбираем 2 значения с минимальными
- 28. Дерево стало таким:
- 29. 5. Снова выбираем 2 значения с минимальными
- 30. Дерево стало таким:
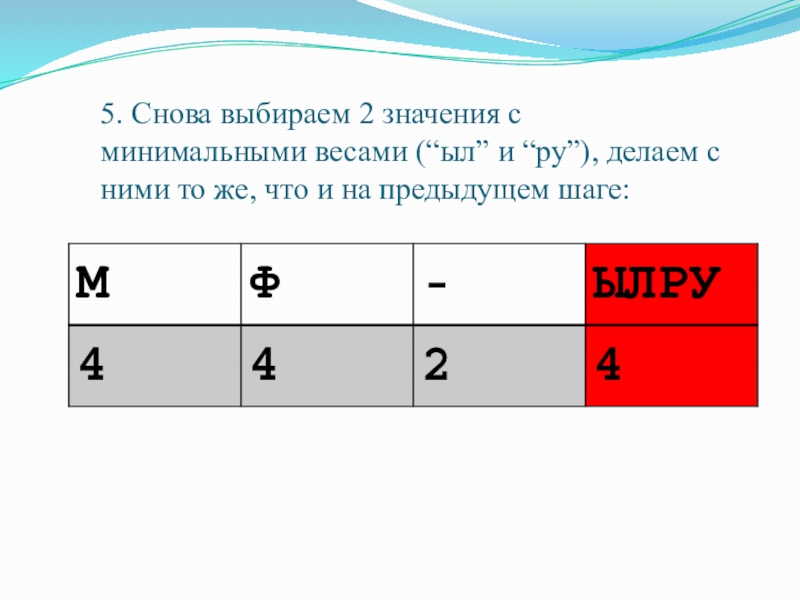
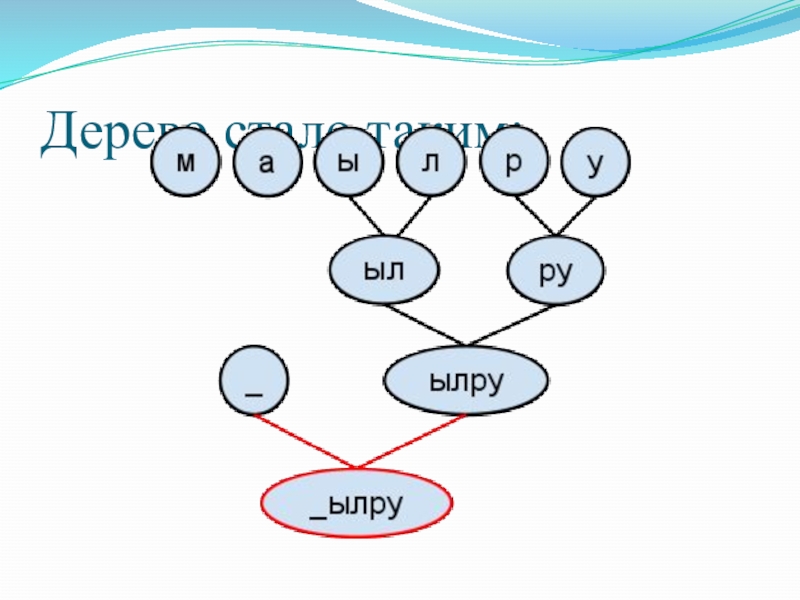
- 31. 6. Снова выбираем 2 значения с минимальными
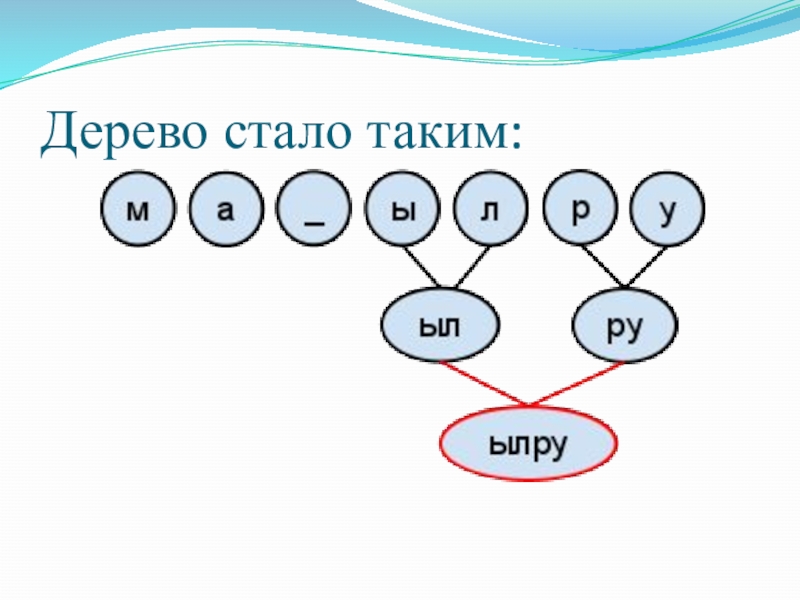
- 32. Дерево стало таким:
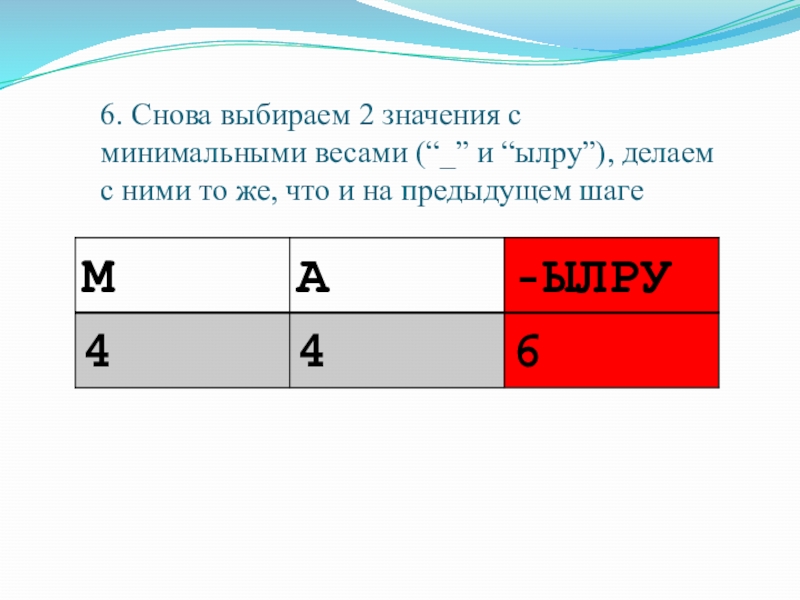
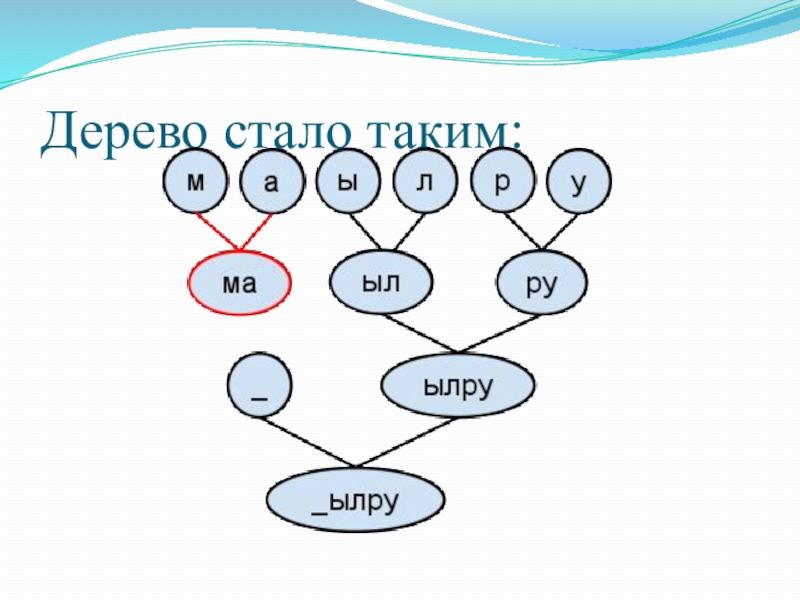
- 33. 7. Снова выбираем 2 значения с минимальными
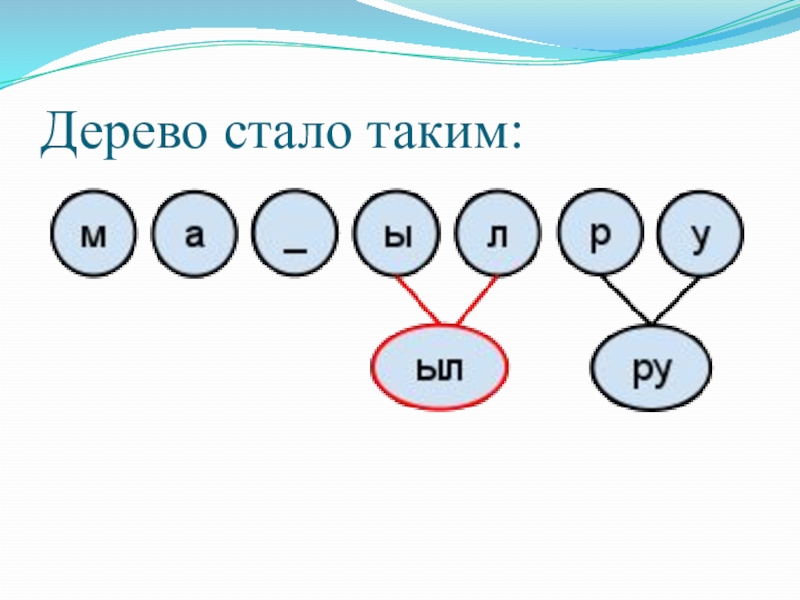
- 34. Дерево стало таким:
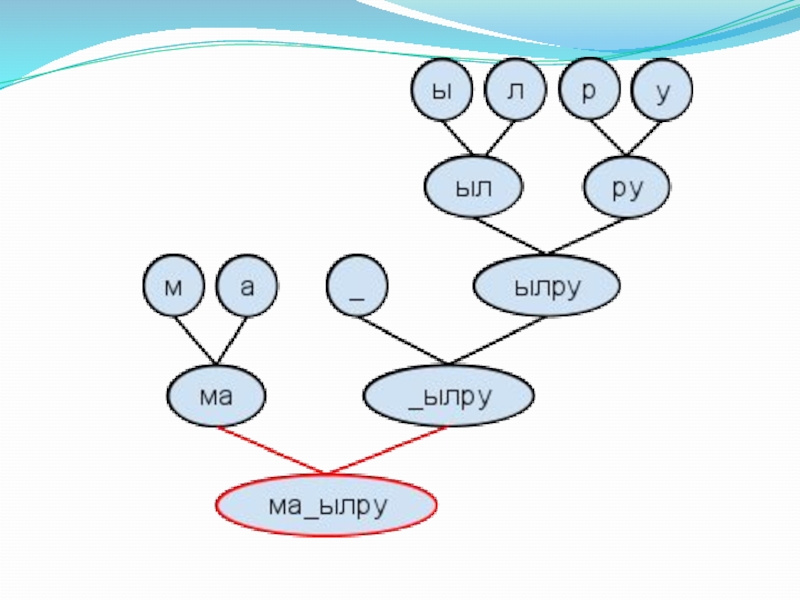
- 35. Последний шаг:
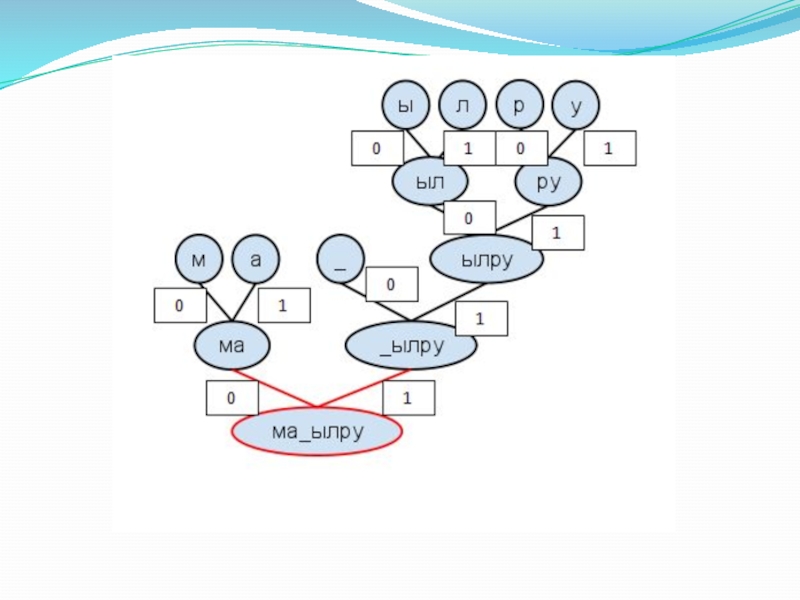
- 36. Слайд 36
- 37. Слайд 37
- 38. РЕЗУЛЬТАТКОЭФФИЦИЕНТ СЖАТИЯ: 112/40=2,8
- 39. Решить самостоятельно:Постройте код Хаффмана для фраз и
- 40. Решить самостоятельно:2. Закодируйте с помощью кода Хаффмана
- 41. Для кодирования сообщения, состоящего из букв А,
- 42. Задача А9. Решение.Построим двоичное дерево, в котором
- 43. Задача А9. Решение.По дереву определим, что для
- 44. Для передачи по каналу связи сообщения, состоящего
- 45. Для 5 букв латинского алфавита заданы их
- 46. Для передачи по каналу связи сообщения, состоящего
- 47. Д/ЗПостройте код Хаффмана для фраз и определить коэффициент сжатия.ОТ_ТОПОТА_КОПЫТ_ПЫЛЬ_ПО_ПОЛЮ_ЛЕТИТШЛА_САША_ПО_ШОССЕ_И СОСАЛА_СУШКУ
Любая информация в компьютере представляется в форме двоичного кода. Чем больше длина этого кода, тем больше места в памяти компьютера он занимает, тем больше времени требуется для его передачи по каналам связи. Все это складывается на
Слайд 2Любая информация в компьютере представляется в форме двоичного кода. Чем больше
длина этого кода, тем больше места в памяти компьютера он занимает, тем больше времени требуется для его передачи по каналам связи.
Все это складывается на производительности компьютера, на эффективности использования компьютерных сетей.
Все это складывается на производительности компьютера, на эффективности использования компьютерных сетей.
Слайд 3Для сокращения объема данных выполняется их сжатие.
Сжатие данных – это процесс,
обеспечивающий уменьшение объема данных за счет изменения способа их организации.
Возможны две ситуации при сжатии:
Потеря информации в результате сжатия недопустимы;
Допустима частичная потеря информации в результате сжатия.
Возможны две ситуации при сжатии:
Потеря информации в результате сжатия недопустимы;
Допустима частичная потеря информации в результате сжатия.
Слайд 4При упаковке данных в файловые архивы производится их сжатие без потери
информации.
Файловые архивы создаются для временного хранения на носителях или передачи по каналам связи. Для работы с этими данными требуется их распаковка (разархивирование), т.е. приведение к первоначальному виду. При этом ни один бит не должен быть потерян.
Файловые архивы создаются для временного хранения на носителях или передачи по каналам связи. Для работы с этими данными требуется их распаковка (разархивирование), т.е. приведение к первоначальному виду. При этом ни один бит не должен быть потерян.
Слайд 5Например:
Если сжатию подвергается текст, то после распаковки в нем не должен
быть искажен ни один символ.
Сжатая программа также должна полностью восстанавливаться, поскольку малейшее искажение приведет ее в неработоспособное состояние.
Сжатая программа также должна полностью восстанавливаться, поскольку малейшее искажение приведет ее в неработоспособное состояние.
Слайд 6Сжатие с частичной потерей информации
Производится при сжатии кода изображения (графики, видео)
и звука.
Слайд 7Сжатие кода графики.
Объем кода можно сократить за счет того, что коды
цвета хранить не для каждого пикселя, а через один, два и т.д. пикселей растра.
Чем больше такие пропуски, тем больше сжимаются данные, но при этом ухудшается качество изображения
Чем больше такие пропуски, тем больше сжимаются данные, но при этом ухудшается качество изображения
Слайд 8Сжатие кода видео.
Быстро меняющиеся фрагменты фильма можно кодировать менее подробно, чем
статические кадры.
Слайд 9Сжатие кода звука.
Поддается труднее всего.
При хорошем качестве записи его объем в
несжатом виде очень большой, а избыточность относительно мала.
Используется психофизиологические особенности человеческого слуха. Учитывается, к каким гармоникам естественного звука наш слух более восприимчив, а к каким – менее. Слабо воспринимаемые гармоники отфильтровываются путем математической обработки. Сжатию также способствует учет нелинейной зависимости между амплитудой звуковых колебаний и восприятием нашим ухом громкости звучания.
Используется психофизиологические особенности человеческого слуха. Учитывается, к каким гармоникам естественного звука наш слух более восприимчив, а к каким – менее. Слабо воспринимаемые гармоники отфильтровываются путем математической обработки. Сжатию также способствует учет нелинейной зависимости между амплитудой звуковых колебаний и восприятием нашим ухом громкости звучания.
Слайд 10Сжатие без потери информации
Первый подход: использование неравномерного кода.
Второй подход: выявление повторяющихся
фрагментов кода.
Слайд 11Использование неравномерного кода.
Символы с меньшим информационным весом, т.е.часто встречающиеся, кодировать более
коротким кодом по сравнению с реже встречающимися символами.
При таком подходе можно существенно сократить объем общего кода текста и, соответственно, места, занимаемого им в памяти компьютера.
При таком подходе можно существенно сократить объем общего кода текста и, соответственно, места, занимаемого им в памяти компьютера.
Слайд 12Одним из простейших, но весьма эффективных способов построения двоичного неравномерно кода,
является алгоритм Дэвида Хаффмана
Слайд 13Алгоритм Хаффмана -
Адаптивный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью.
Был разработан 1952 году аспирантом Массачусетского технологического
института Дэвидом Хаффманом при написании им курсовой работы. В настоящее время используется во многих программах сжатия данных.
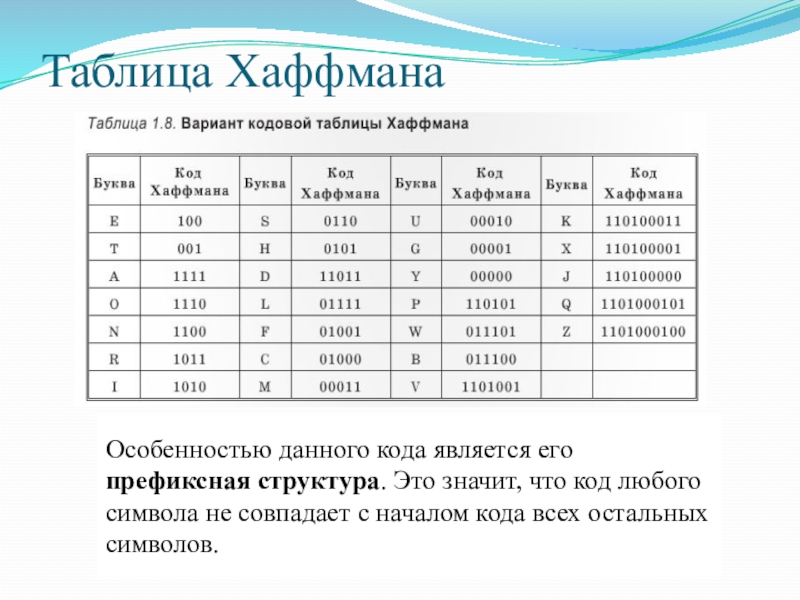
Слайд 14Таблица Хаффмана
В этой таблице буквы расположены в порядке убывания частоты повторяемости
в тексте. Самые часто используемые в текстах буквы «Е» и «Т» имеют коды размером 3 бита, а самые редкие буквы «Q» и «Z» – 10 битов.
Особенностью данного кода является его префиксная структура. Это значит, что код любого символа не совпадает с началом кода всех остальных символов.
Слайд 15Префиксные коды
Чтобы понять, как строятся префиксные коды, рассмотрим, как построить ориентированный
граф, определяющий этот код.
Например, кодовые слова 00, 01, 10, 011, 100, 101, 1001, 1010, 1111, кодируют соответственно буквы: a, b, c, d, e, f, g, h, i.
Например, кодовые слова 00, 01, 10, 011, 100, 101, 1001, 1010, 1111, кодируют соответственно буквы: a, b, c, d, e, f, g, h, i.
Слайд 16Префиксные коды
Построим граф этого кода.
Из начальной вершины выходят две дуги, помеченные
0 и 1. Затем из конца каждой такой дуги входят новые дуги, помеченные 0 и 1 так, чтобы, идя по этим дугам от корня, читалось начало какого-либо кодового слова.
Слайд 17Префиксные коды
Если при этом какая-то последовательность оказывается прочитанной полностью, то у
конца последней дуги пишется кодируемый символ.
Из получившихся вершин снова проводятся дуги — и так далее, до тех пор, пока не будут исчерпаны все коды.
Слайд 19Коэффициентом сжатия называют отношение длины кода в байтах после сжатия к
его длине до сжатия.
В данном примере: коэффициент сжатия = 16/29 0,55
Раскодирование (распаковка) текста производится с помощью двоичного дерева кодирования Хаффмана.
Деревом называется графическое представление (граф) структуры связей между элементами некоторой системы.
Двоичным деревом называется дерево, в котором любая вершина, имеет не более двух потомков.
Корнем дерева называется единственная вершина, не имеющая родительской вершины.
Листьями дерева называются вершины, не имеющие потомков.
В данном примере: коэффициент сжатия = 16/29 0,55
Раскодирование (распаковка) текста производится с помощью двоичного дерева кодирования Хаффмана.
Деревом называется графическое представление (граф) структуры связей между элементами некоторой системы.
Двоичным деревом называется дерево, в котором любая вершина, имеет не более двух потомков.
Корнем дерева называется единственная вершина, не имеющая родительской вершины.
Листьями дерева называются вершины, не имеющие потомков.
Слайд 22Пример: Предположим, что необходимо выполнить сжатие текстового документа с фразой “мама_мыла_раму”. Наш
исходный текст “весит” 112 бит, так как каждый символ занимает 8 бит в кодовой таблице, а таких символов у нас 14 штук.
Слайд 231. Составляем таблицу частот, то есть, подсчитываем количество вхождений каждой буквы
во фразу, в результате чего получим вес каждой буквы:
Слайд 253. Выбираем 2 значения с минимальными весами (“р” и “у”), суммируем
их веса и заменяем эти значения в таблице одним объединенным значением:
Слайд 274. Снова выбираем 2 значения с минимальными весами (“ы” и “л”),
делаем с ними то же, что и на предыдущем шаге:
Слайд 295. Снова выбираем 2 значения с минимальными весами (“ыл” и “ру”),
делаем с ними то же, что и на предыдущем шаге:
Слайд 316. Снова выбираем 2 значения с минимальными весами (“_” и “ылру”),
делаем с ними то же, что и на предыдущем шаге
Слайд 337. Снова выбираем 2 значения с минимальными весами (“м” и “а”),
делаем с ними то же, что и на предыдущем шаге:
Слайд 39Решить самостоятельно:
Постройте код Хаффмана для фраз и определить коэффициент сжатия.
Карл_ у_клары_украл_
кораллы, а_клара_У_карла_украла_кларнет
НА_ ДВОРЕ_ ТРАВА,_ НА_ ТРАВЕ_ ДРОВА
НА_ ДВОРЕ_ ТРАВА,_ НА_ ТРАВЕ_ ДРОВА
Слайд 40Решить самостоятельно:
2. Закодируйте с помощью кода Хаффмана следующий текст:
HAPPYNEWYEAR
3. Расшифруйте с
помощью двоичного дерева Хаффмана следующий код:
11110111 10111100 00011100 00101100
10010011 01110100 11001111 11101101
001100
11110111 10111100 00011100 00101100
10010011 01110100 11001111 11101101
001100
Слайд 41Для кодирования сообщения, состоящего из букв А, Б, В, Г и
Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность.
А–00, Б–010, В–011, Г–101, Д–111.
Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно?
Выберите правильный вариант ответа.
1) для буквы Б – 01 2) это невозможно
3) для буквы В – 01 4) для буквы Г – 01
А–00, Б–010, В–011, Г–101, Д–111.
Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно?
Выберите правильный вариант ответа.
1) для буквы Б – 01 2) это невозможно
3) для буквы В – 01 4) для буквы Г – 01
Задача А9
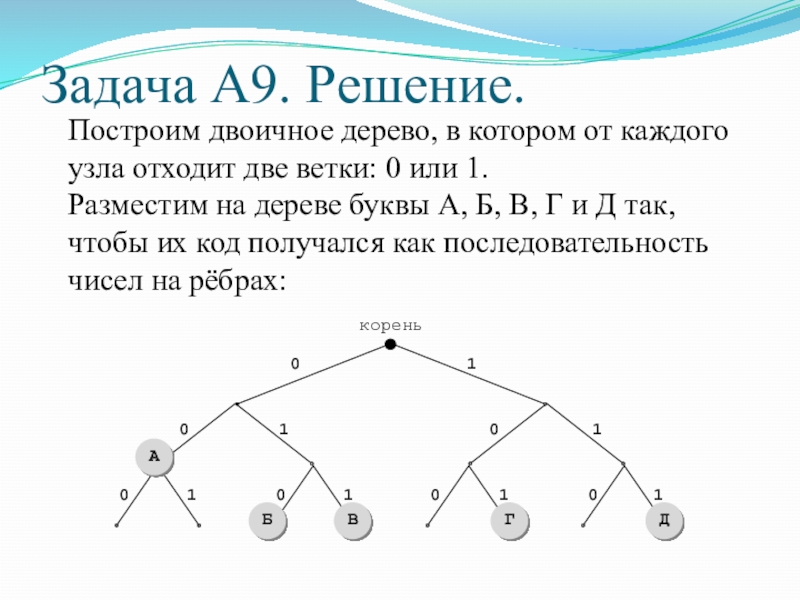
Слайд 42Задача А9. Решение.
Построим двоичное дерево, в котором от каждого узла отходит
две ветки: 0 или 1.
Разместим на дереве буквы А, Б, В, Г и Д так, чтобы их код получался как последовательность чисел на рёбрах:
Разместим на дереве буквы А, Б, В, Г и Д так, чтобы их код получался как последовательность чисел на рёбрах:
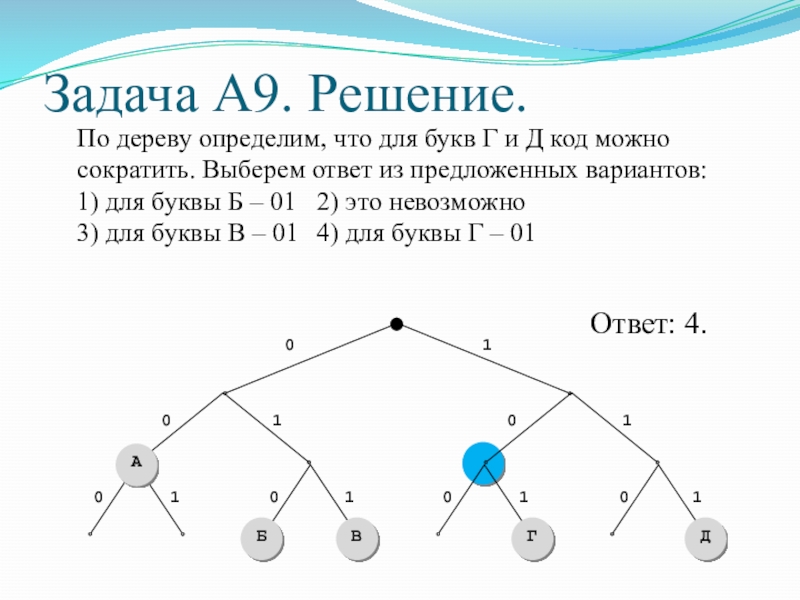
Слайд 43Задача А9. Решение.
По дереву определим, что для букв Г и Д
код можно сократить. Выберем ответ из предложенных вариантов:
1) для буквы Б – 01 2) это невозможно
3) для буквы В – 01 4) для буквы Г – 01
1) для буквы Б – 01 2) это невозможно
3) для буквы В – 01 4) для буквы Г – 01
Ответ: 4.
Слайд 44Для передачи по каналу связи сообщения, состоящего только из букв А,
Б, В, Г, решили использовать неравномерный по длине код:
A=0, Б=10, В=110.
Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?
1) 1 2) 1110 3) 111 4) 11
A=0, Б=10, В=110.
Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?
1) 1 2) 1110 3) 111 4) 11
Для самостоятельной работы
Слайд 45Для 5 букв латинского алфавита заданы их двоичные коды.
Эти коды
представлены в таблице:
Задача А9
Определить, какой набор букв закодирован двоичной строкой 0110100011000
Слайд 46Для передачи по каналу связи сообщения, состоящего только из букв А,
Б, В, Г, решили использовать неравномерный по длине код:
A=0, Б=10, В=110.
Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?
A=0, Б=10, В=110.
Как нужно закодировать букву Г, чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?
Задача А9
Слайд 47Д/З
Постройте код Хаффмана для фраз и определить коэффициент сжатия.
ОТ_ТОПОТА_КОПЫТ_ПЫЛЬ_ПО_ПОЛЮ_ЛЕТИТ
ШЛА_САША_ПО_ШОССЕ_И СОСАЛА_СУШКУ
