- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Системы счисления
Содержание
- 1. Презентация по информатике на тему Системы счисления
- 2. Системой счисления или нумерацией называется определенный способ
- 3. Основные понятия позиционных систем счисленияЦифра –
- 4. Основная формулаВ позиционной системе счисления с основанием
- 5. Традиционная система счисления - системы счисления, в
- 6. Двоичная система счисления.Перевод целых чиселДвоичная система:
- 7. Общее правило перевода чисел в систему с
- 8. Арифметические операциисложениевычитание0+0=0 0+1=11+0=1 1+1=1021 + 1 +
- 9. умножениеделение 1 0 1 0 12×
- 10. Плюсы и минусы двоичной системынужны технические устройства
- 11. Восьмеричная система10 → 88 → 10100100 =
- 12. Перевод в двоичную систему и обратно8102трудоемко2 действия8
- 13. Перевод из двоичной системы в восьмеричнуюШаг 1.
- 14. Арифметические операции в восьмеричной системе счислениясложение1 5
- 15. Арифметические операции в восьмеричной системе счислениявычитание4 5
- 16. Шестнадцатеричная системаОснование (количество цифр): 16Алфавит: 0, 1,
- 17. Перевод в двоичную систему и обратно16102трудоемко2 действия16
- 18. Перевод из двоичной системы в шестнадцатеричную10010111011112Шаг 1.
- 19. Перевод в восьмеричную систему и обратнотрудоемко3DEA16 =
- 20. Арифметические операции в шестнадцатеричной системе счислениясложениеA 5
- 21. Арифметические операции в шестнадцатеричной системе счислениявычитаниеС 5
- 22. ВыводыПеревод чисел из десятичной системы счисления в
- 23. Закрепление материала1. Перевести из десятичной в 2-ую,
Слайд 1СИСТЕМЫ СЧИСЛЕНИЯ
Бюджетное профессиональное образовательное учреждение Вологодской области
«Череповецкий многопрофильный колледж»
Разработчик:
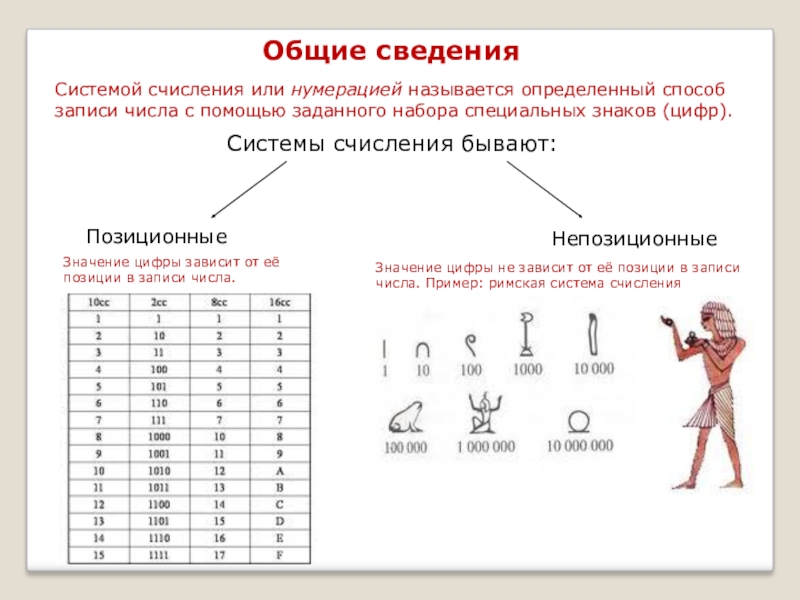
Слайд 2Системой счисления или нумерацией называется определенный способ записи числа с помощью
Системы счисления бывают:
Позиционные
Непозиционные
Общие сведения
Значение цифры не зависит от её позиции в записи числа. Пример: римская система счисления
Значение цифры зависит от её позиции в записи числа.
Слайд 3Основные понятия позиционных
систем счисления
Цифра – символ, используемый для записи числа.
Алфавит
Размерность алфавита (основание) – количество цифр в алфавите.
Разряд числа – каждая позиция в записи числа
разряды : 3 2 1 0 -1 -2 -3 6248,547
Развернутая форма записи числа
2348310 = 2 · 104 + 3 · 103 + 4 · 102 + 8 · 101 + 3 · 100.
10001102 = 1 · 26 + 0 · 25 + 0 · 24 + 0 · 23 + 1 · 22 + 1 · 21 + 0 · 20;
7А0С16 = 7 · 163 + 10 · 162 + 0 · 161 + 12 · 160.
Базис системы счисления - последовательность чисел, каждое
из которых задает “вес” соответствующих разрядов.
…105,104,103,102,101,100,10-1,10-2,10-3,10-4,10-5 …
Таким образом «разложить число по базису системы счисления» - это представить число в развернутой форме.
Слайд 4Основная формула
В позиционной системе счисления с основанием q любое число может
Aq =±(an–1×qn–1+ an–2 × qn–2+…+ a0 × q0+ a–1×q–1+…+ a–m× q–m)
Здесь:
А — число;
q — основание системы счисления;
ai — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
qi — «вес» i-го разряда.
Такая запись числа называется развёрнутой формой записи.
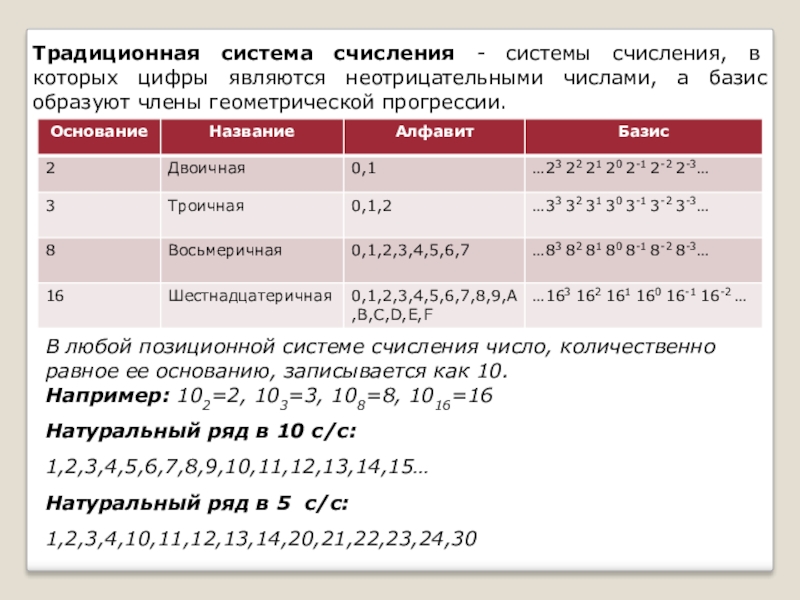
Слайд 5Традиционная система счисления - системы счисления, в которых цифры являются неотрицательными
В любой позиционной системе счисления число, количественно
равное ее основанию, записывается как 10.
Например: 102=2, 103=3, 108=8, 1016=16
Натуральный ряд в 10 с/с:
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15…
Натуральный ряд в 5 с/с:
1,2,3,4,10,11,12,13,14,20,21,22,23,24,30
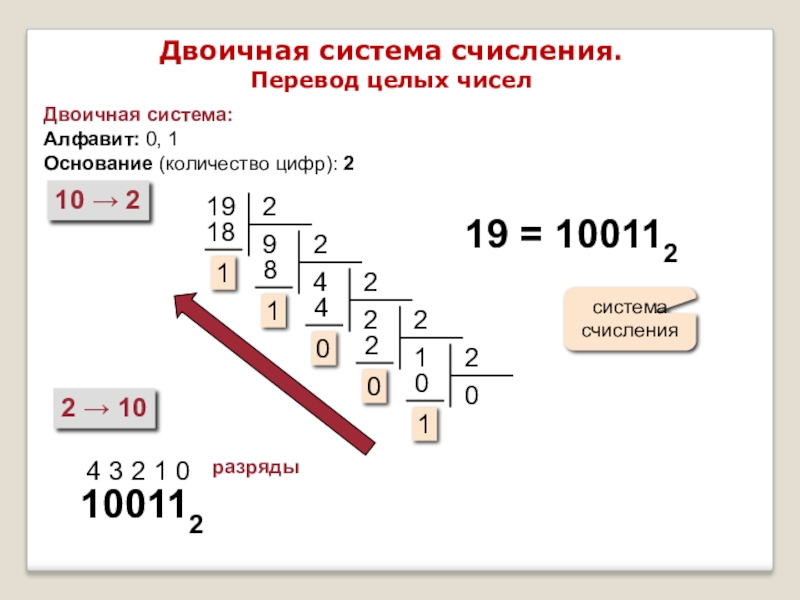
Слайд 6Двоичная система счисления.
Перевод целых чисел
Двоичная система:
Алфавит: 0, 1
Основание (количество цифр):
10 → 2
2 → 10
19
19 = 100112
система счисления
100112
4 3 2 1 0
разряды
Слайд 7Общее правило перевода чисел в систему
с основанием q
1) последовательно выполнять
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.
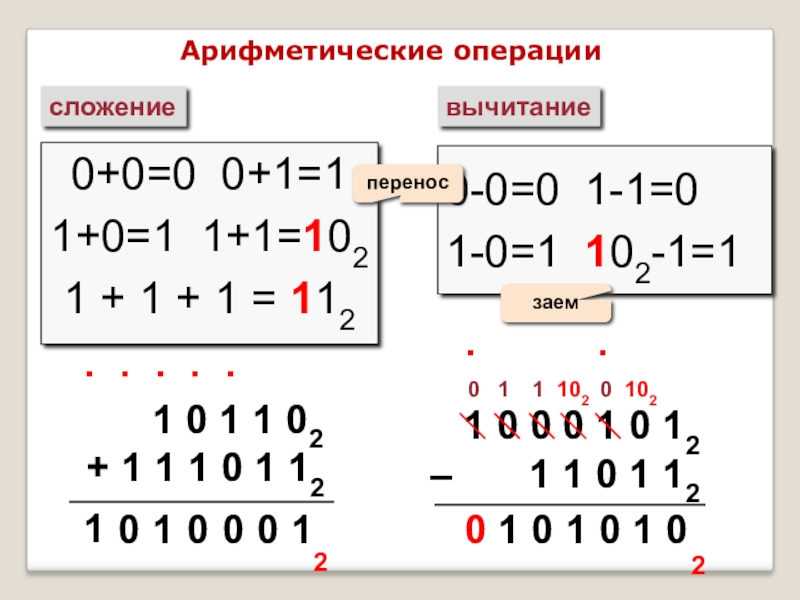
Слайд 8Арифметические операции
сложение
вычитание
0+0=0 0+1=1
1+0=1 1+1=102
1 + 1 + 1 = 112
0-0=0 1-1=0
1-0=1
перенос
заем
1 0 1 1 02
+ 1 1 1 0 1 12
1
∙
0
0
∙
0
1
1
0
2
1 0 0 0 1 0 12
– 1 1 0 1 12
1
∙
∙
0 102
1
0
0 1 1 102
0
1
0
∙
∙
∙
Слайд 9
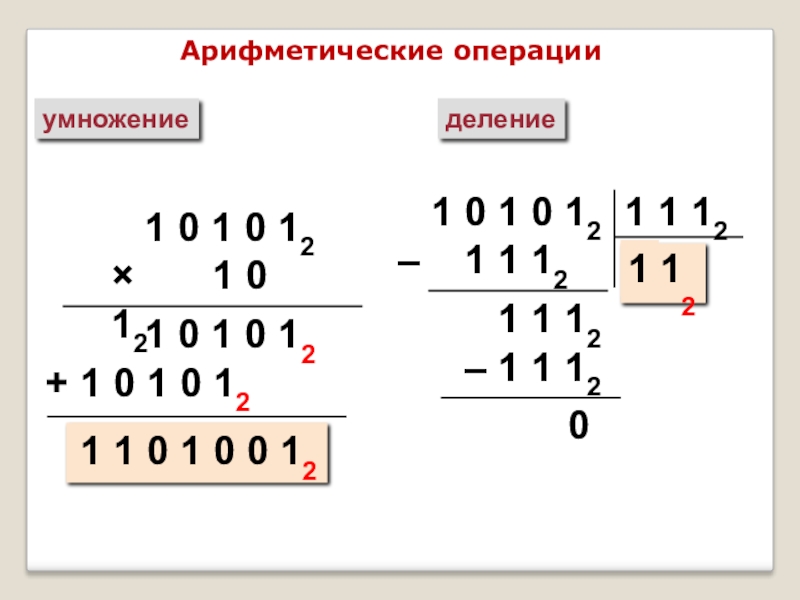
умножение
деление
1 0 1 0 12
× 1
1 0 1 0 12
+ 1 0 1 0 12
1 1 0 1 0 0 12
1 0 1 0 12
– 1 1 12
1 1 12
1
1 1 12
– 1 1 12
0
Арифметические операции
Слайд 10Плюсы и минусы двоичной системы
нужны технические устройства только с двумя устойчивыми
надежность и помехоустойчивость двоичных кодов;
выполнение операций с двоичными числами для компьютера намного проще, чем с десятичными.
простые десятичные числа записываются в виде бесконечных двоичных дробей;
двоичные числа имеют много разрядов;
запись числа в двоичной системе однородна,
то есть содержит только нули и единицы; поэтому человеку сложно ее воспринимать.
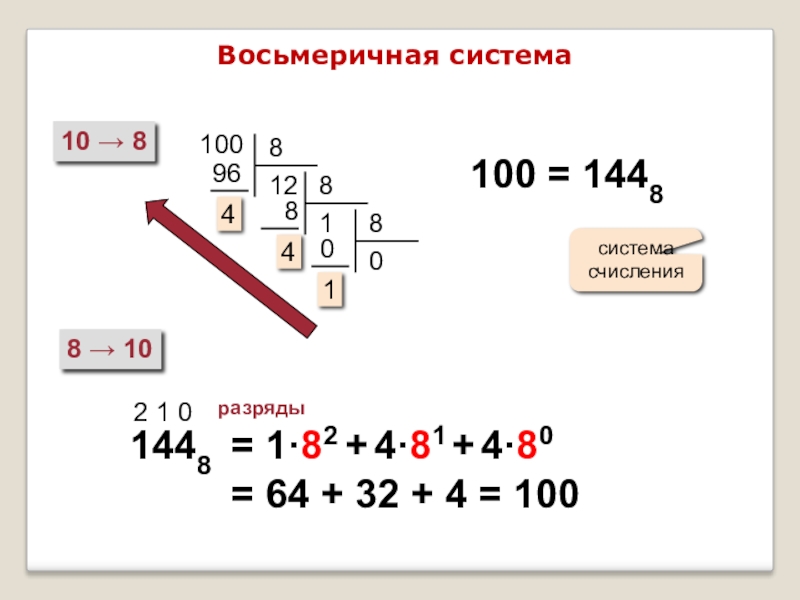
Слайд 11Восьмеричная система
10 → 8
8 → 10
100
100 = 1448
система счисления
1448
2
разряды
= 1·82 + 4·81 + 4·80
= 64 + 32 + 4 = 100
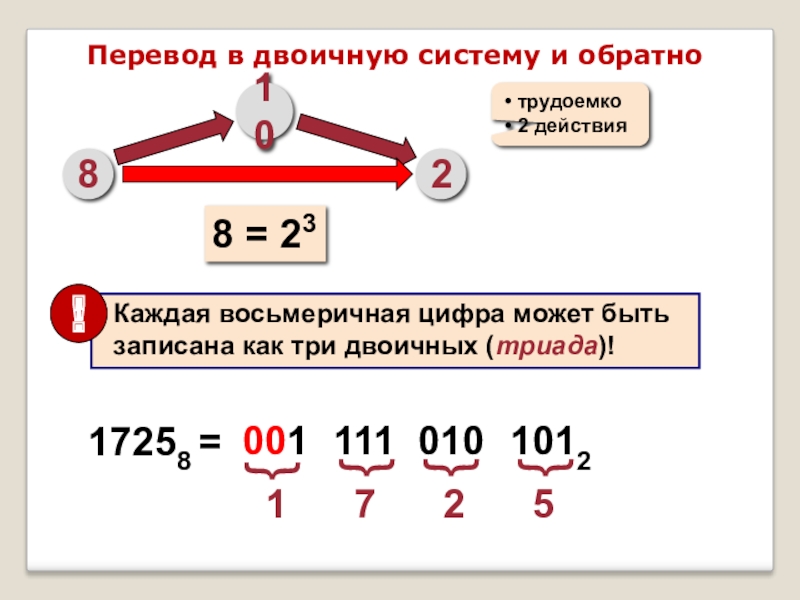
Слайд 12Перевод в двоичную систему и обратно
8
10
2
трудоемко
2 действия
8 = 23
17258 =
1
001
111
010
1012
{
{
{
{
Слайд 13Перевод из двоичной системы
в восьмеричную
Шаг 1. Разбить на триады, начиная
001 001 011 101 1112
Шаг 2. Каждую триаду записать одной
восьмеричной цифрой:
1
3
5
7
Ответ: 10010111011112 = 113578
001 001 011 101 1112
1
Дописать необходимое число нулей
Слайд 14Арифметические операции в восьмеричной
системе счисления
сложение
1 5 68
+ 6
∙
1
6 + 2 = 8 = 8 + 0
5 + 6 + 1 = 12 = 8 + 4
1 + 6 + 1 = 8 = 8 + 0
∙
1 в перенос
∙
08
0
4
1 в перенос
Слайд 15Арифметические операции в восьмеричной
системе счисления
вычитание
4 5 68
– 2
∙
(6 + 8) – 7 = 7
(5 – 1 + 8) – 7 = 5
(4 – 1) – 2 = 1
∙
заем
78
1
5
заем
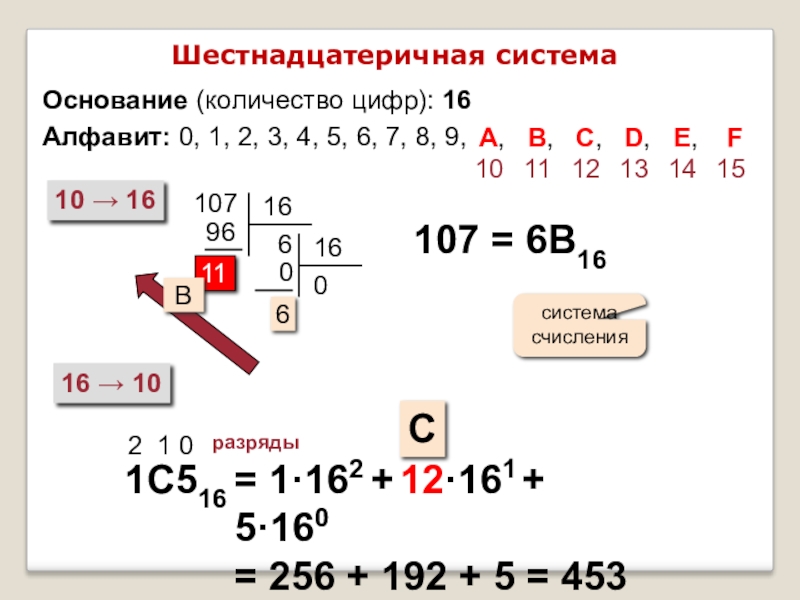
Слайд 16Шестнадцатеричная система
Основание (количество цифр): 16
Алфавит: 0, 1, 2, 3, 4, 5,
10 → 16
16 → 10
107
107 = 6B16
система счисления
1C516
2 1 0
разряды
= 1·162 + 12·161 + 5·160
= 256 + 192 + 5 = 453
A,
10
B,
11
C,
12
D,
13
E,
14
F
15
B
C
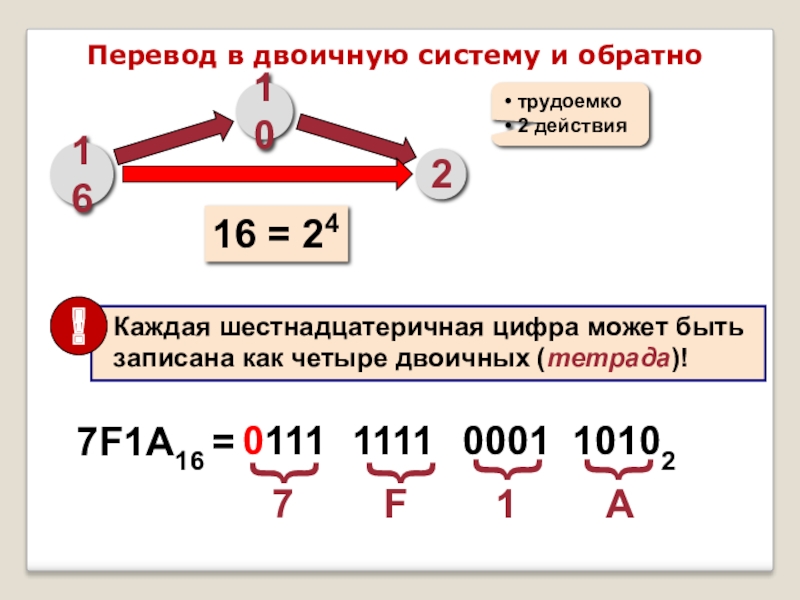
Слайд 17Перевод в двоичную систему и обратно
16
10
2
трудоемко
2 действия
16 = 24
7F1A16 =
7
0111
{
{
1111
0001
10102
{
{
Слайд 18Перевод из двоичной системы
в шестнадцатеричную
10010111011112
Шаг 1. Разбить на тетрады, начиная
0001 0010 1110 11112
Шаг 2. Каждую тетраду записать одной
шестнадцатеричной цифрой:
0001 0010 1110 11112
1
2
E
F
Ответ: 10010111011112 = 12EF16
Дописать необходимое число нулей
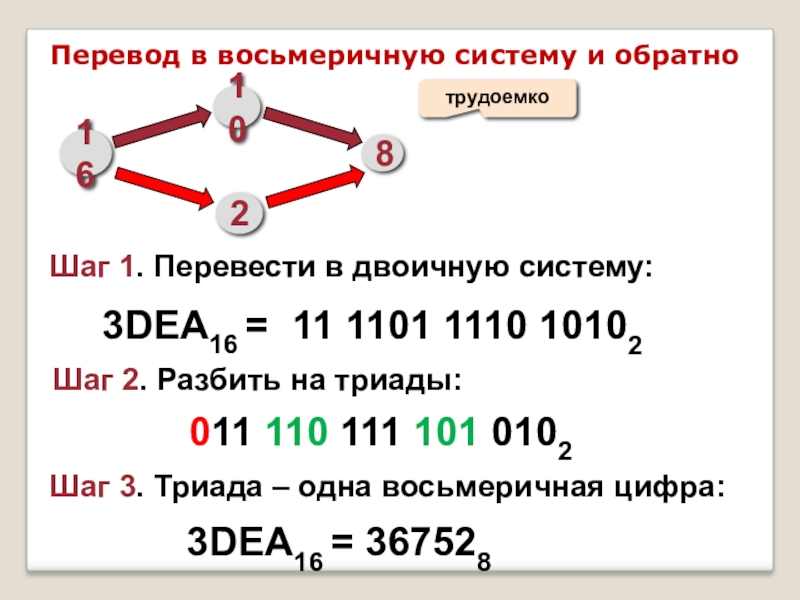
Слайд 19Перевод в восьмеричную систему и обратно
трудоемко
3DEA16 =
11 1101 1110 10102
16
10
8
2
Шаг
Шаг 2. Разбить на триады:
Шаг 3. Триада – одна восьмеричная цифра:
011 110 111 101 0102
3DEA16 = 367528
Слайд 20Арифметические операции в
шестнадцатеричной системе счисления
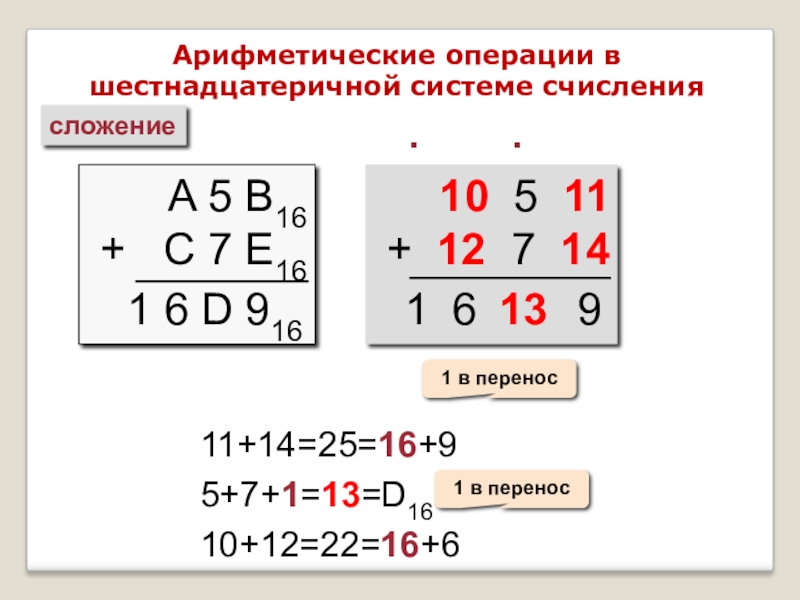
сложение
A 5 B16
+ C 7
∙
1 6 D 916
10 5 11
+ 12 7 14
11+14=25=16+9
5+7+1=13=D16
10+12=22=16+6
∙
1 в перенос
1 в перенос
13
9
6
1
Слайд 21Арифметические операции в
шестнадцатеричной системе счисления
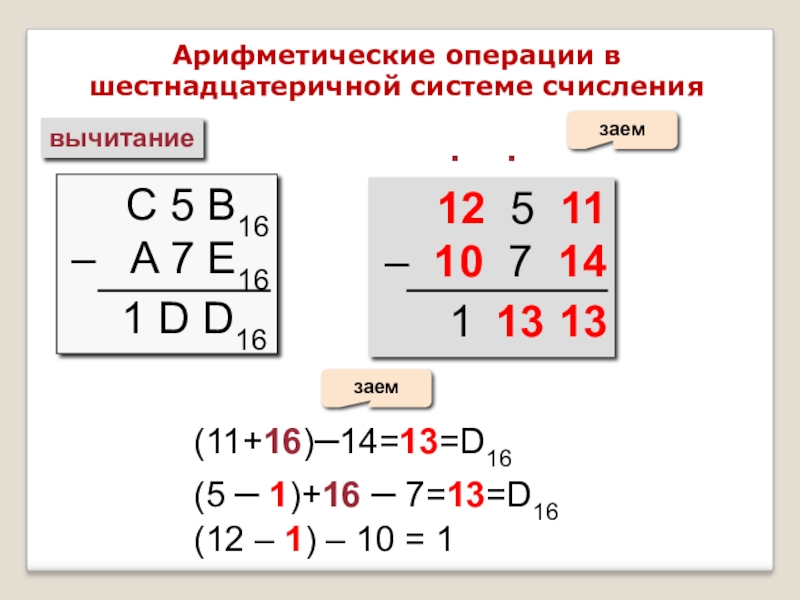
вычитание
С 5 B16
– A 7
заем
∙
1 D D16
12 5 11
– 10 7 14
∙
(11+16)–14=13=D16
(5 – 1)+16 – 7=13=D16
(12 – 1) – 10 = 1
заем
13
1
13
Слайд 22Выводы
Перевод чисел из десятичной системы счисления в другую производится путем деления
Перевод чисел из двоичной системы счисления в восьмеричную или щестнадцатеричную системы производится путем разбития числа на триады и тетрады, используя таблицы восьмеричных и шестнадцатеричных чисел.
Слайд 23Закрепление материала
1. Перевести из десятичной в 2-ую, 8-ую и 16-ую систему
2. Перевести из двоичной в 10-ую, 8-ую и 16-ую систему счисления: 100011111110102; 1101010012; 1011111101000012.
3. Расставьте в порядке возрастания: 558 ; 5516 ; 1012 ; a116 .
4. Выполните сложение и вычитание между следующими парами чисел:
101100100112 и 111011012;
2538 и 178;
1а16 и 1716