- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Логические основы компьютеров
Содержание
- 1. Презентация по информатике на тему Логические основы компьютеров
- 2. Булева алгебраДвоичное кодирование – все виды информации
- 3. Логические высказыванияЛогическое высказывание – это повествовательное предложение,
- 4. Обозначение высказыванийA – Сейчас идет дождь.B –
- 5. Таблица истинности логического выражения Х – это
- 6. Операция НЕ (инверсия)Если высказывание A истинно, то
- 7. Операция И (логическое умножение, конъюнкция)10также: A·B, A
- 8. Операция ИЛИ (логическое сложение, дизъюнкция)10также: A+B, A
- 9. Импликация ("если …, то …")Высказывание "A →
- 10. Эквиваленция ("тогда и только тогда, …")Высказывание "A
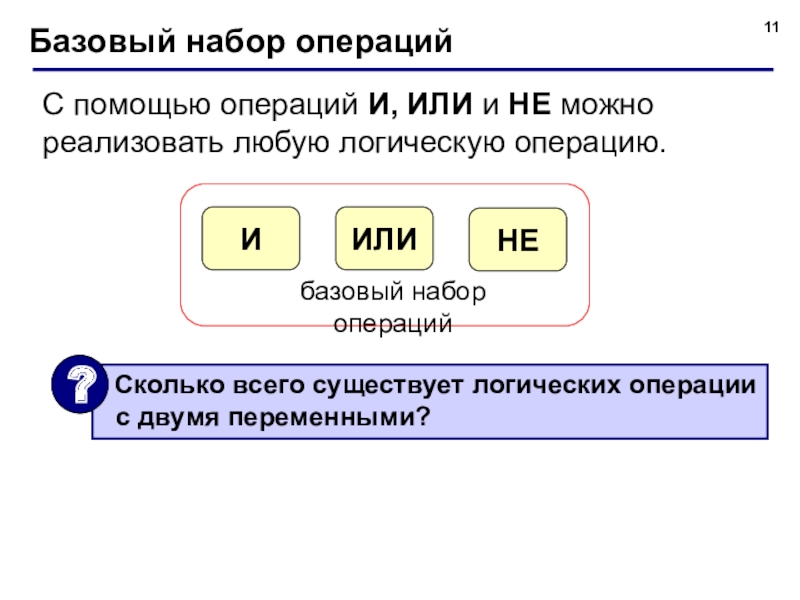
- 11. Базовый набор операцийС помощью операций И, ИЛИ и НЕ можно реализовать любую логическую операцию.
- 12. Логические формулыСистема имеет три датчика и может
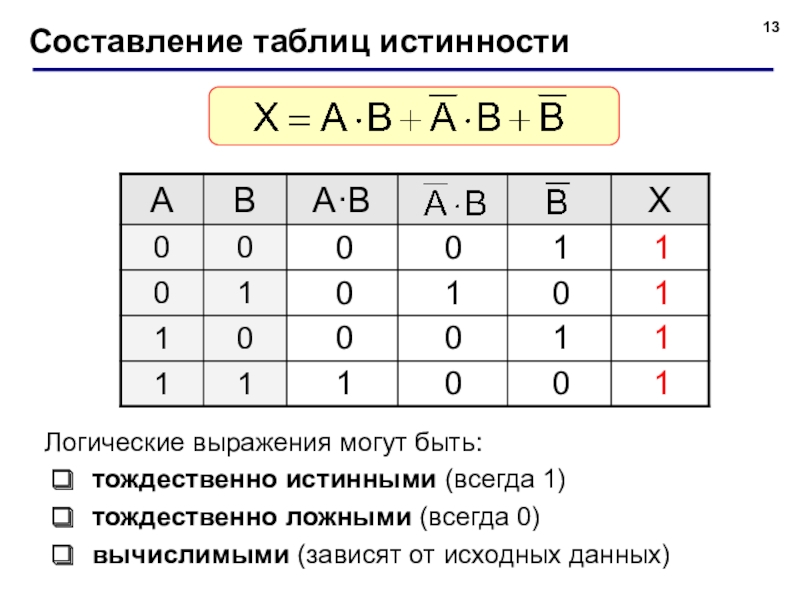
- 13. Составление таблиц истинностиЛогические выражения могут быть:тождественно истинными (всегда 1)тождественно ложными (всегда 0)вычислимыми (зависят от исходных данных)
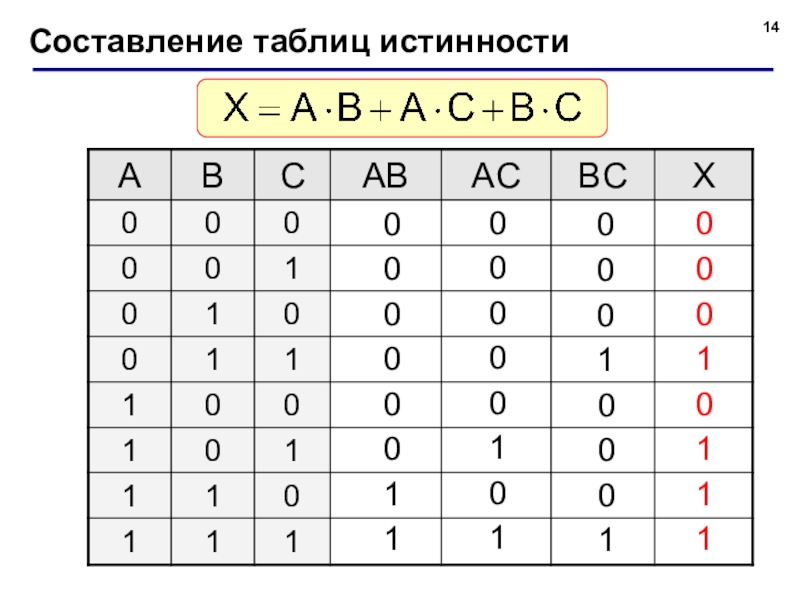
- 14. Составление таблиц истинности
- 15. Домашнее задание:Составить таблицу истинности для логической формулы:
- 16. Графическое отображение логических высказываний
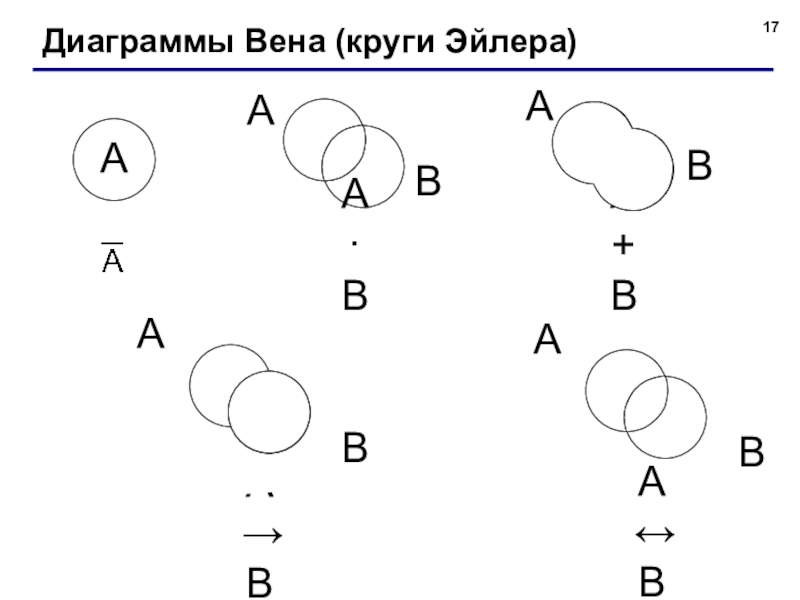
- 17. Диаграммы Вена (круги Эйлера)A·BA+BA→BA↔B
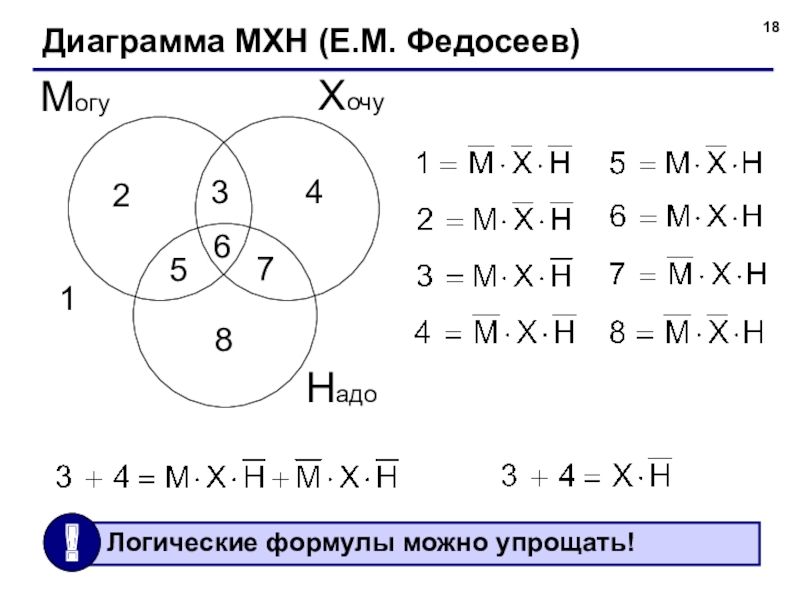
- 18. Диаграмма МХН (Е.М. Федосеев)ХочуМогуНадо12345678
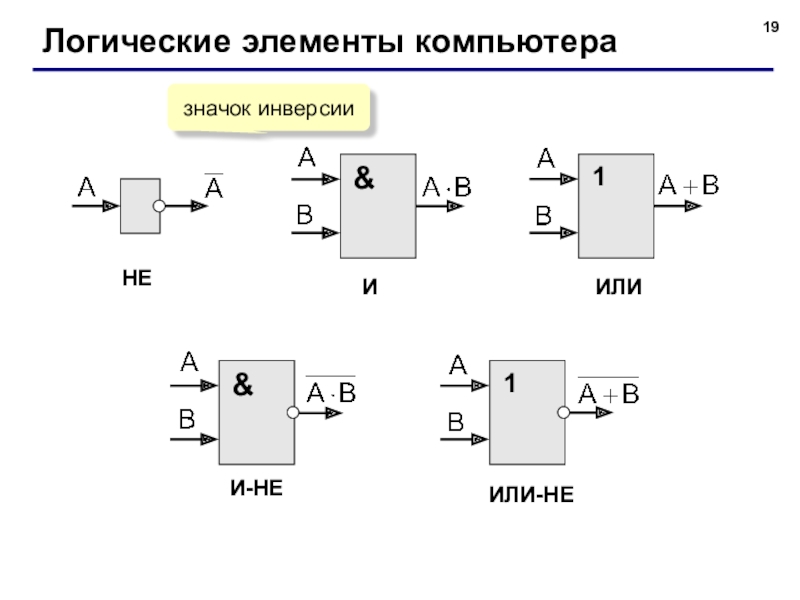
- 19. Логические элементы компьютераНЕИИЛИИЛИ-НЕИ-НЕзначок инверсии
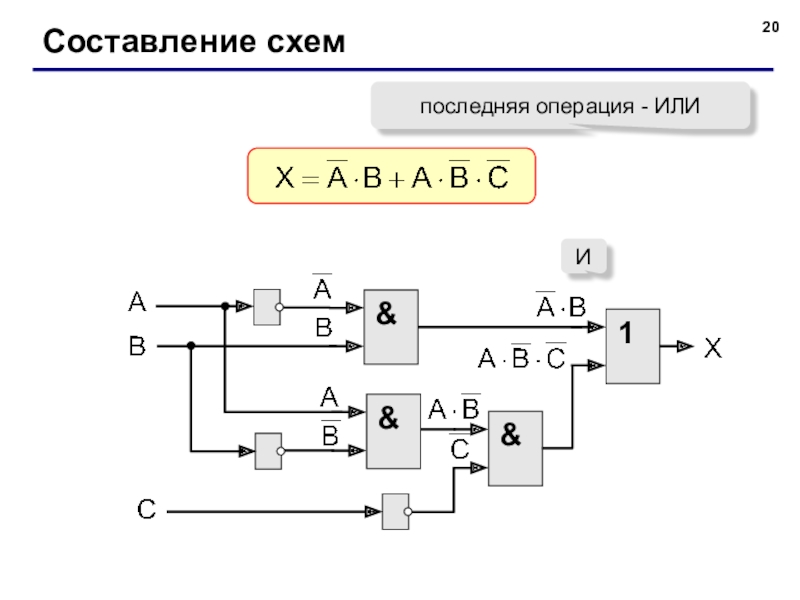
- 20. Составление схемпоследняя операция - ИЛИ&И
- 21. Триггер (англ. trigger – защёлка)Триггер – это
- 22. ПолусумматорПолусумматор – это логическая схема, способная складывать
- 23. СумматорСумматор – это логическая схема, способная складывать два одноразрядных двоичных числа с переносом из предыдущего разряда.Σсуммапереносперенос
- 24. Табличный методЗадача 2. Дочерей Василия Лоханкина зовут
Слайд 2Булева алгебра
Двоичное кодирование – все виды информации кодируются с помощью 0
Задача – разработать оптимальные правила обработки таких данных.
Джордж Буль разработал основы алгебры, в которой используются только 0 и 1 (алгебра логики, булева алгебра).
Почему "логика"? Результат выполнения операции можно представить как истинность (1) или ложность (0) некоторого высказывания.
Слайд 3Логические высказывания
Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно
Высказывание или нет?
Мы изучаем информатику.
Жирафы летят на север.
История – интересный предмет.
У квадрата – 10 сторон и все разные.
Красиво!
В городе N живут 2 миллиона человек.
Который час?
Слайд 4Обозначение высказываний
A – Сейчас идет дождь.
B – Форточка открыта.
простые высказывания (элементарные)
Составные
A и B
A или не B
если A, то B
не A и B
A тогда и только
тогда, когда B
Сейчас идет дождь и открыта форточка.
Сейчас идет дождь или форточка закрыта.
Если сейчас идет дождь, то форточка открыта.
Сейчас нет дождя и форточка открыта.
Дождь идет тогда и только тогда, когда открыта форточка.
Слайд 5Таблица истинности логического выражения Х – это таблица, где в левой
Таблицы истинности
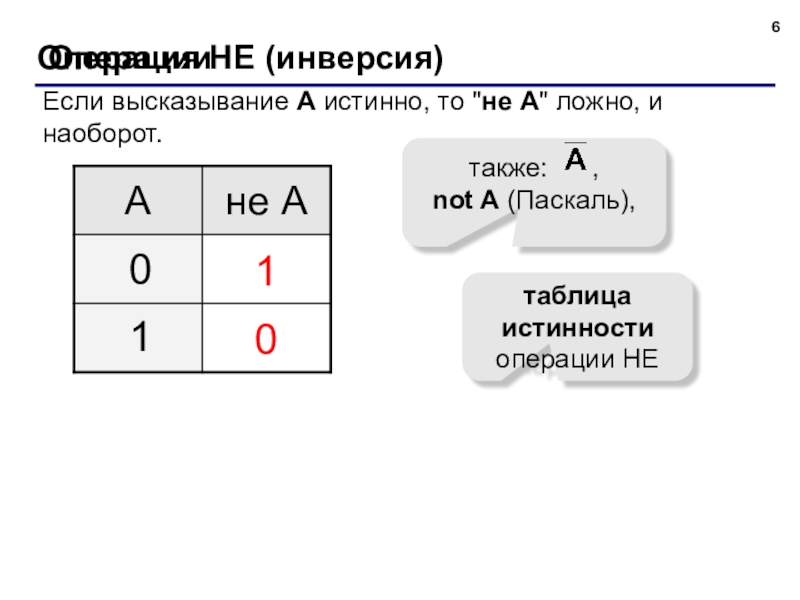
Слайд 6Операция НЕ (инверсия)
Если высказывание A истинно, то "не А" ложно, и
1
0
0
1
таблица истинности операции НЕ
также: ,
not A (Паскаль),
Операции
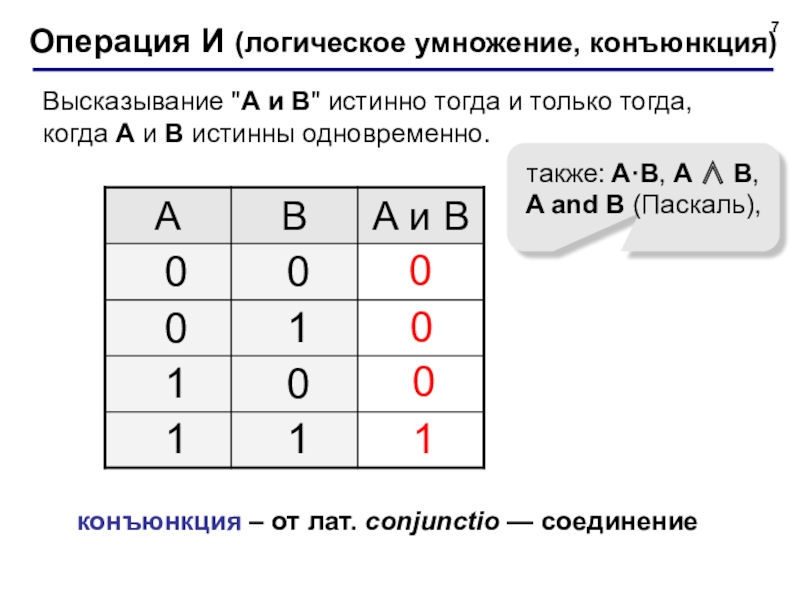
Слайд 7Операция И (логическое умножение, конъюнкция)
1
0
также: A·B, A ∧ B,
A and B
0
0
конъюнкция – от лат. conjunctio — соединение
Высказывание "A и B" истинно тогда и только тогда, когда А и B истинны одновременно.
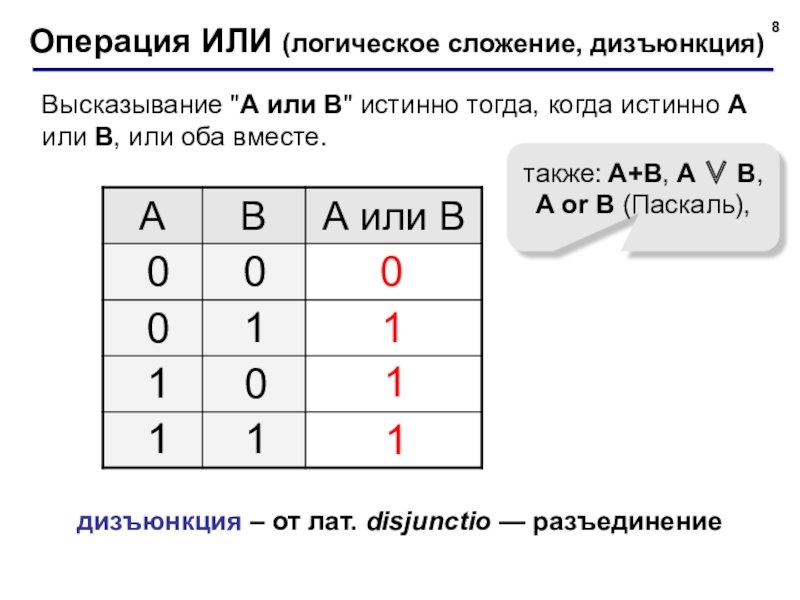
Слайд 8Операция ИЛИ (логическое сложение, дизъюнкция)
1
0
также: A+B, A ∨ B,
A or B
1
1
дизъюнкция – от лат. disjunctio — разъединение
Высказывание "A или B" истинно тогда, когда истинно А или B, или оба вместе.
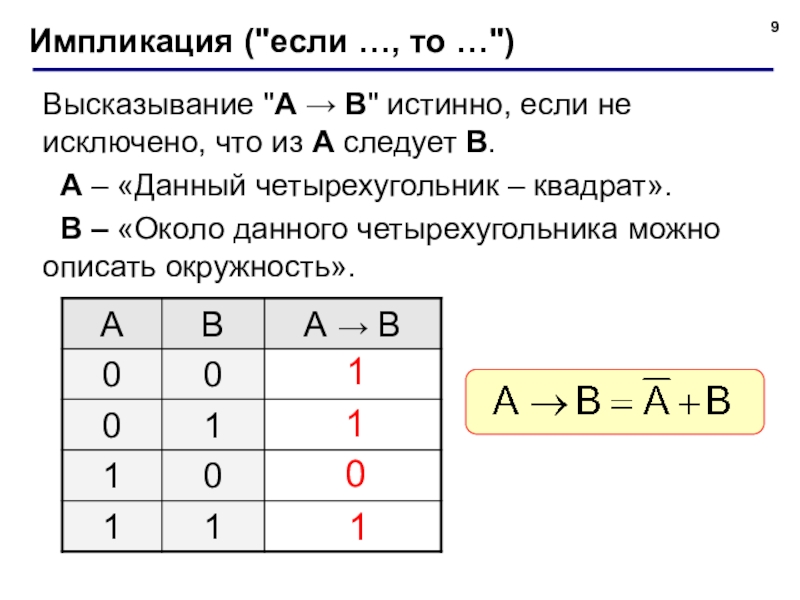
Слайд 9Импликация ("если …, то …")
Высказывание "A → B" истинно, если не
A – «Данный четырехугольник – квадрат».
B – «Около данного четырехугольника можно описать окружность».
1
1
1
0
Слайд 10Эквиваленция ("тогда и только тогда, …")
Высказывание "A ↔ B" истинно тогда
Слайд 11Базовый набор операций
С помощью операций И, ИЛИ и НЕ можно реализовать
Слайд 12Логические формулы
Система имеет три датчика и может работать, если два из
A – "Датчик № 1 неисправен".
B – "Датчик № 2 неисправен".
C – "Датчик № 3 неисправен".
Аварийный сигнал:
X – "Неисправны два датчика".
X – "Неисправны датчики № 1 и № 2" или
"Неисправны датчики № 1 и № 3" или
"Неисправны датчики № 2 и № 3".
логическая формула
Слайд 13Составление таблиц истинности
Логические выражения могут быть:
тождественно истинными (всегда 1)
тождественно ложными (всегда
вычислимыми (зависят от исходных данных)
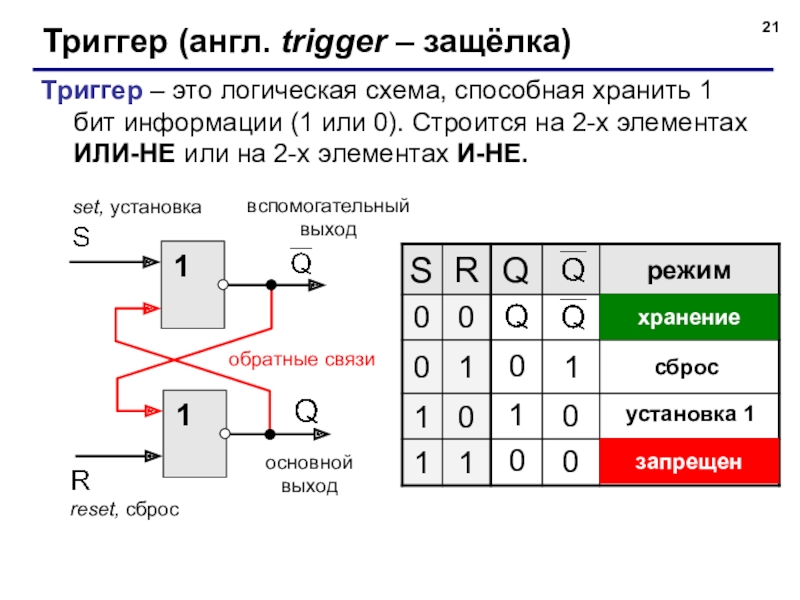
Слайд 21Триггер (англ. trigger – защёлка)
Триггер – это логическая схема, способная хранить
основной
выход
вспомогательный
выход
reset, сброс
set, установка
обратные связи
1
1
0
0
0
0
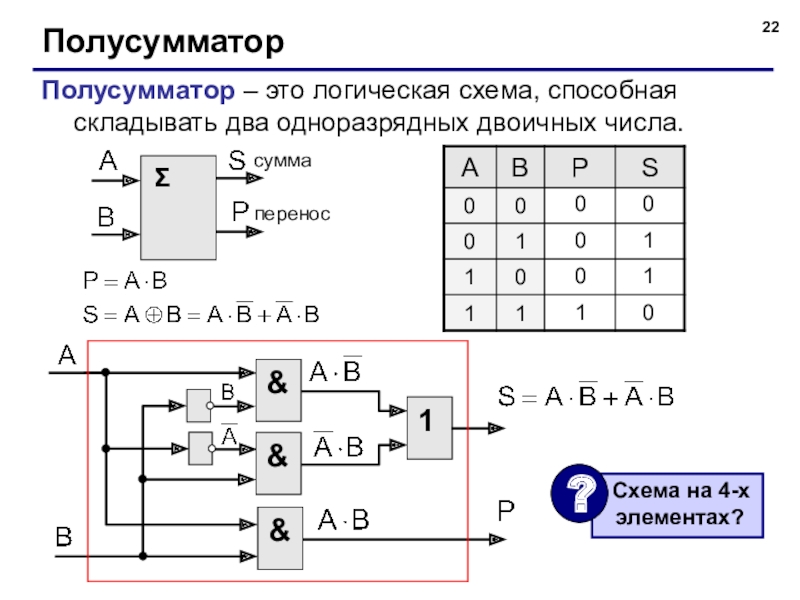
Слайд 22Полусумматор
Полусумматор – это логическая схема, способная складывать два одноразрядных двоичных числа.
0
0 1
0 1
1 0
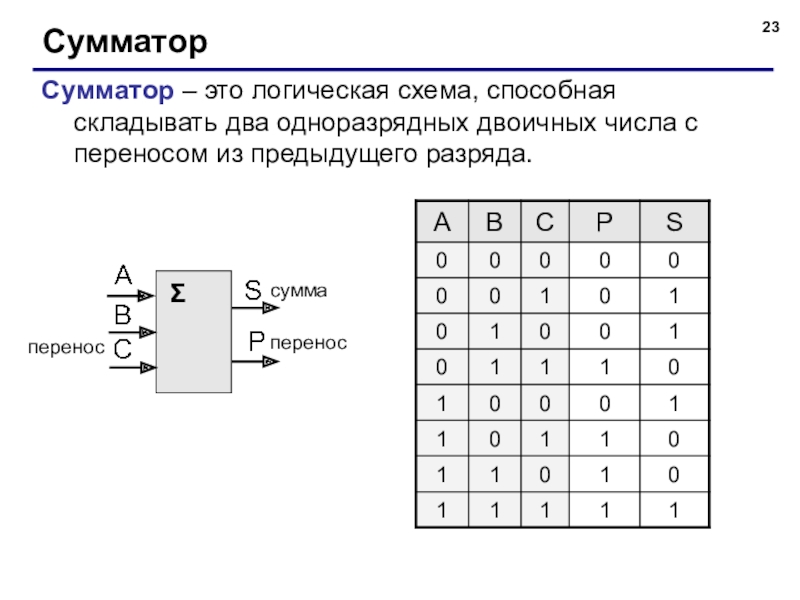
Слайд 23Сумматор
Сумматор – это логическая схема, способная складывать два одноразрядных двоичных числа
Σ
сумма
перенос
перенос
Слайд 24Табличный метод
Задача 2. Дочерей Василия Лоханкина зовут Даша, Анфиса и Лариса.
Даша живет не в Париже, а Лариса – не в Ростове,
парижанка – не актриса,
в Ростове живет певица,
Лариса – не балерина.
0
0
0
0
1
0
0
0
1
0
0
1
1
0
1
0
0
1
Много вариантов.
Есть точные данные.