- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике на тему Арифметические операции в позиционных системах 10 класс
Содержание
- 1. Презентация по информатике на тему Арифметические операции в позиционных системах 10 класс
- 2. Ключевые словапозиционные системы счисленияарифметические операции в системе счисления с основанием qтаблица сложениятаблица умножения
- 3. Таблицы сложения в двоичной, троичной и восьмеричной
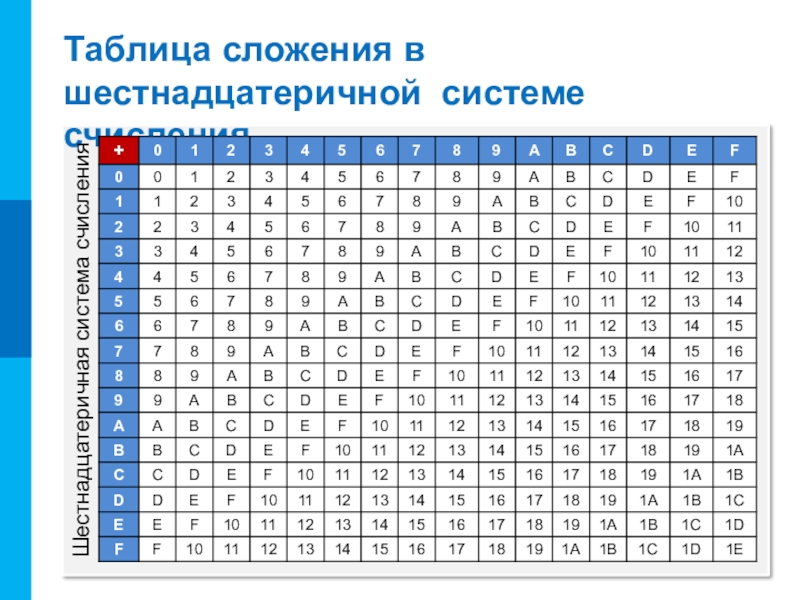
- 4. Таблица сложения в шестнадцатеричной системе счисленияШестнадцатеричная система счисления
- 5. 1Чтобы в системе счисления с основанием q
- 6. 1 + 2 = 3 ≥ 3
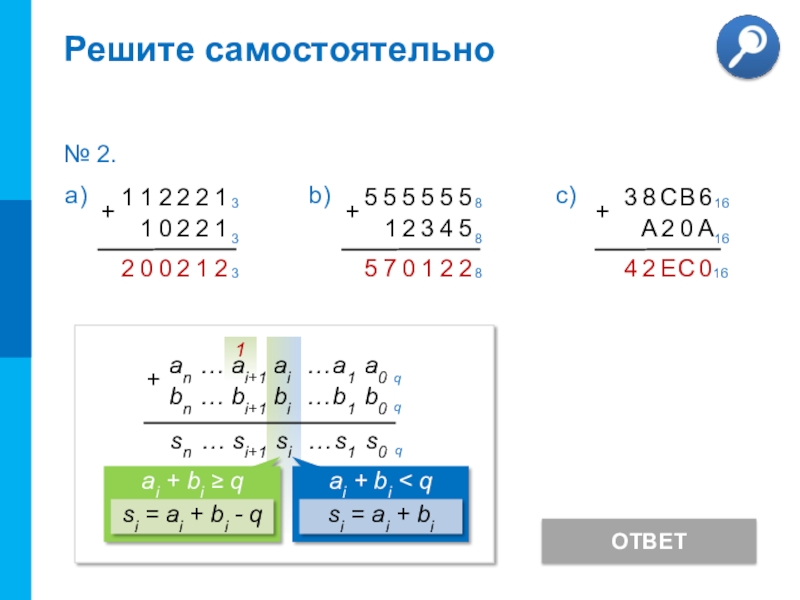
- 7. Решите самостоятельноОТВЕТ№ 2.
- 8. ●Чтобы в системе счисления с основанием q
- 9. 0 = 0 записываем 0 под 4-м
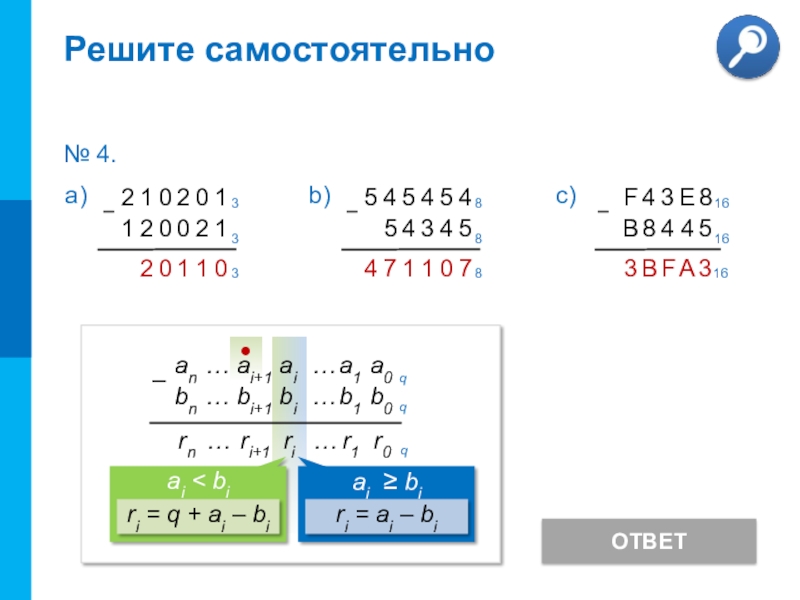
- 10. Решите самостоятельноОТВЕТ№ 4.
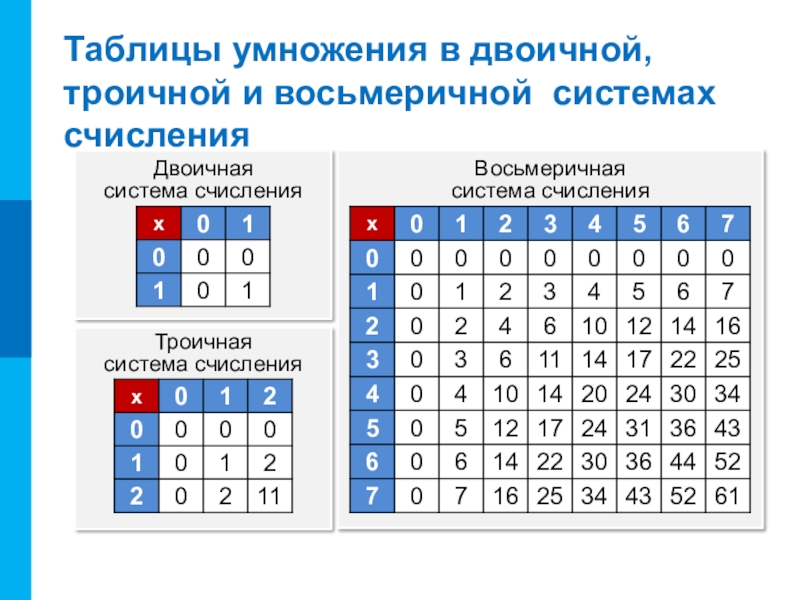
- 11. Таблицы умножения в двоичной, троичной и восьмеричной
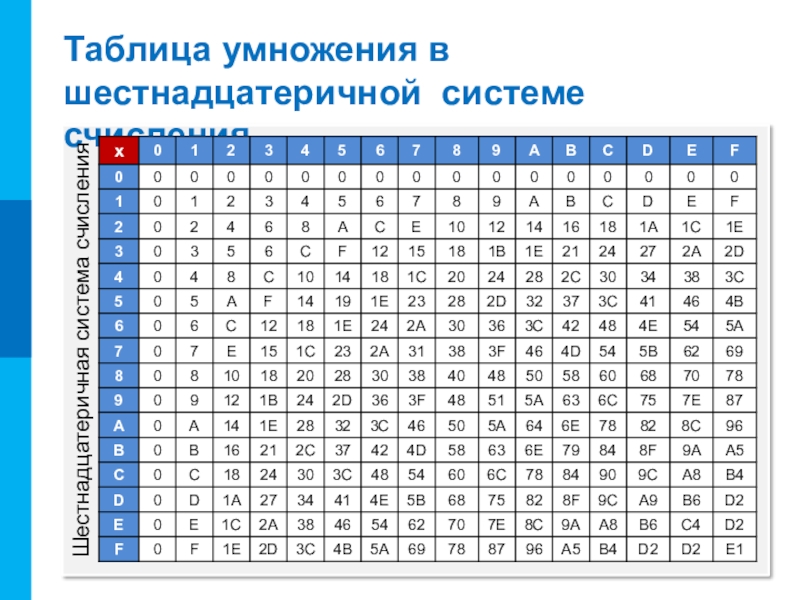
- 12. Таблица умножения в шестнадцатеричной системе счисленияШестнадцатеричная система счисления
- 13. ai · b div qЧтобы в системе
- 14. 1 · 2 + 1 = 3
- 15. Решите самостоятельноОТВЕТ№ 6.
- 16. Деление нельзя свести к поразрядным операциям над
- 17. Деление чисел в системе счисления с
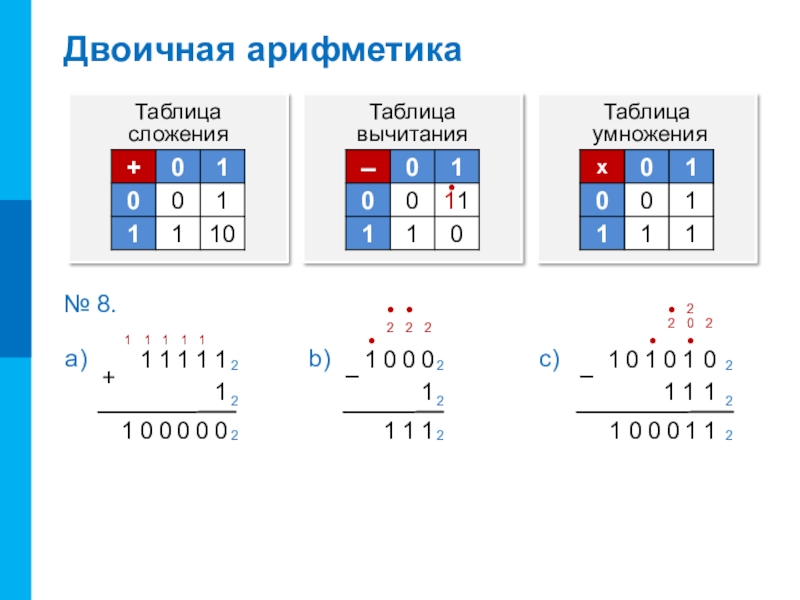
- 18. Двоичная арифметика●00000 1112а) 111 ●2b) 1●●№ 8. 1122200011●2c) 1●220●2
- 19. Исходное выражение 24000 + 42016 + 22018
- 20. Вопросы и заданияДля работы с десятичными числами
- 21. Вопросы и заданияЗадание 2. Найдём количество цифр
- 22. Самое главноеАрифметические операции в позиционных системах счисления
- 23. Самое главноеДля работы с десятичными числами вида
- 24. Вопросы и задания1. Выполните арифметические операции над
- 25. Вопросы и задания2. Какое число следует за
- 26. Вопросы и задания3. Сумму восьмеричных чисел 17
- 27. Вопросы и задания4. Какая первая цифра в
Слайд 1АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ
В ПОЗИЦИОННЫХ СИСТЕМАХ СЧИСЛЕНИЯ
ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В КОМПЬЮТЕРЕ
Слайд 2Ключевые слова
позиционные системы счисления
арифметические операции в системе счисления с основанием q
таблица
таблица умножения
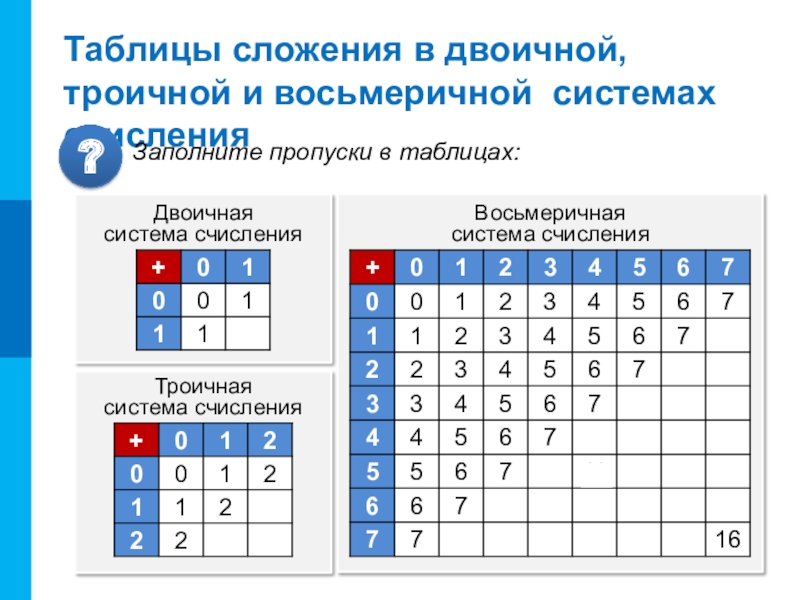
Слайд 3Таблицы сложения в двоичной, троичной и восьмеричной системах счисления
Двоичная
система счисления
Восьмеричная
система
Троичная
система счисления
Заполните пропуски в таблицах:
?
Слайд 51
Чтобы в системе счисления с основанием q получить сумму S двух
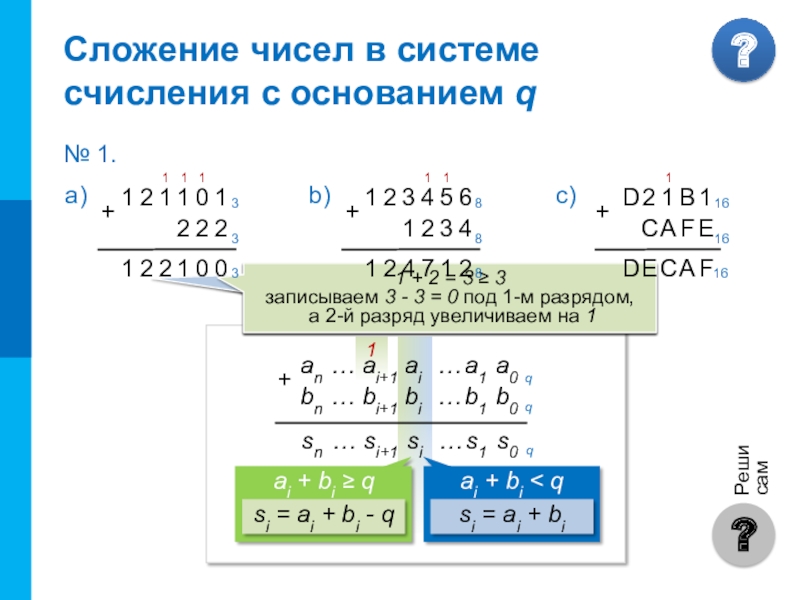
Сложение чисел в системе счисления
с основанием q
если ai + bi < q, то si = ai + bi,
старший (i + 1)-й разряд не изменяется
если ai + bi ≥ q, то si = ai + bi – q,
старший (i + 1)-й разряд увеличивается на 1
Слайд 61 + 2 = 3 ≥ 3 записываем 3 – 3 =
1 + 1 + 2 = 4 ≥ 3
записываем 4 – 3 = 1 под 3-м разрядом,
а 4-й разряд увеличиваем на 1
1 + 1 = 2 < 3
записываем 2 под 4-м разрядом
1 + 2 = 3 ≥ 3
записываем 3 - 3 = 0 под 1-м разрядом,
а 2-й разряд увеличиваем на 1
1
2
4
7
1
2
1
1
8
b)
D
E
C
A
F
1
16
c)
Сложение чисел в системе
счисления с основанием q
3
а)
?
Реши сам
№ 1.
1
2
2
1
0
0
1
1
1
Слайд 8●
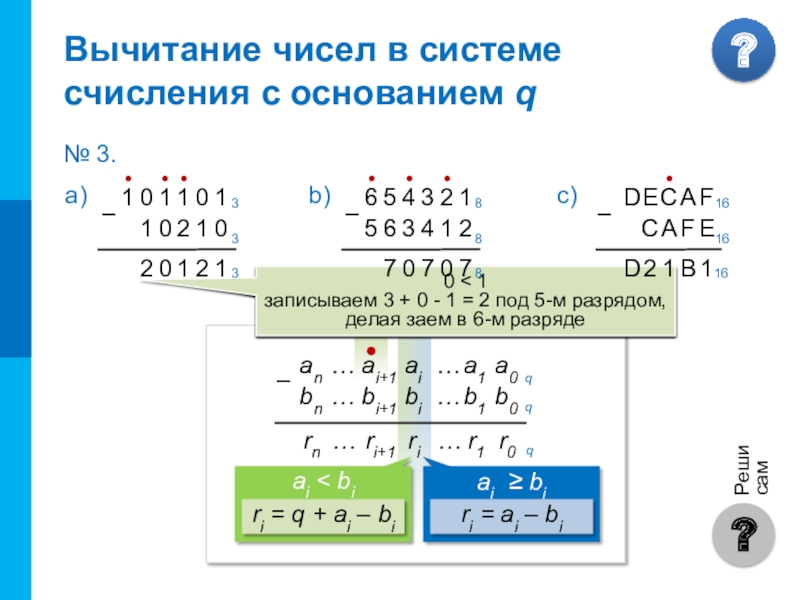
Чтобы в системе счисления с основанием q получить разность R двух
Вычитание чисел в системе счисления
с основанием q
если ai ≥ bi, то ri = ai – bi,
старший (i + 1)-й разряд не изменяется
если a i < b i , то ri = q + ai – bi ,
старший (i + 1)-й разряд уменьшается на 1
Слайд 90 = 0
записываем 0 под 4-м разрядом
0 < 2
записываем 3 +
0 < 1
записываем 3 + 0 – 1 = 2 под 2-м разрядом,
делая заем в 3-м разряде
1 ≥ 0
записываем 1 - 0 = 1 под 1-м разрядом
0 < 1
записываем 3 + 0 - 1 = 2 под 5-м разрядом,
делая заем в 6-м разряде
Вычитание чисел в системе
счисления с основанием q
?
Реши сам
2
0
1
2
1
●
●
3
а)
7
0
7
0
7
●
8
b)
D
2
1
B
1
●
16
c)
●
●
●
№ 3.
Слайд 11Таблицы умножения в двоичной, троичной и восьмеричной системах счисления
Двоичная
система счисления
Восьмеричная
система
Троичная
система счисления
Слайд 13ai · b div q
Чтобы в системе счисления q получить произведение
Умножение многозначного числа на однозначное в системе счисления q
если ai · b < q, то mi = ai · b,
старший (i + 1)-й разряд не изменяется
если ai · b ≥ q, то mi = ai · b mod q,
старший (i + 1)-й разряд увеличивается на ai · b div q
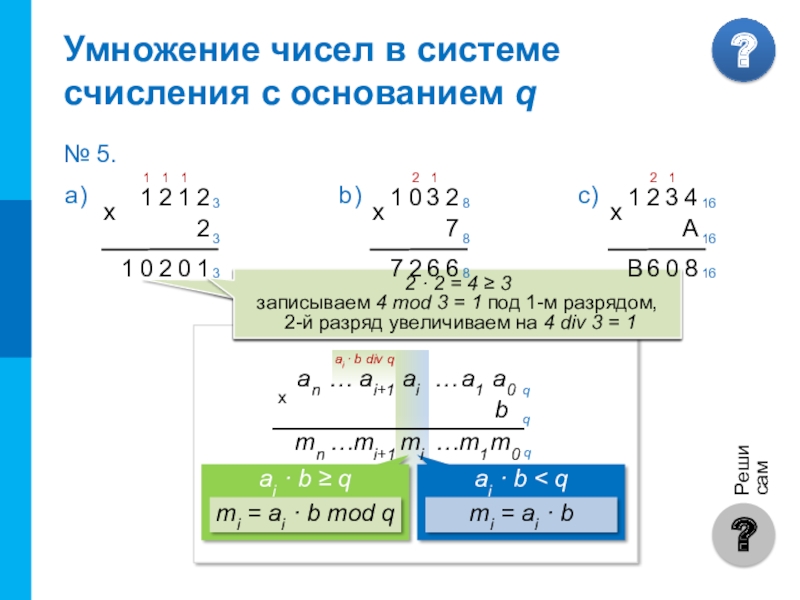
Слайд 141 · 2 + 1 = 3 ≥ 3 записываем 3 mod
2 · 2 + 1 = 3 ≥ 3
записываем 5 mod 3 = 2 под 3-м разрядом,
4-й разряд увеличиваем на 5 div 3 = 1
2 · 1 + 1 = 3 ≥ 3
записываем 3 mod 3 = 0 под 4-м разрядом
и в 5-й разряд записываем 3 div 3 = 1
2 · 2 = 4 ≥ 3
записываем 4 mod 3 = 1 под 1-м разрядом,
2-й разряд увеличиваем на 4 div 3 = 1
Умножение чисел в системе
счисления с основанием q
3
а)
7
2
6
6
2
1
8
b)
?
Реши сам
№ 5.
1
0
2
0
1
1
1
1
В
6
0
8
2
1
16
с)
Слайд 16
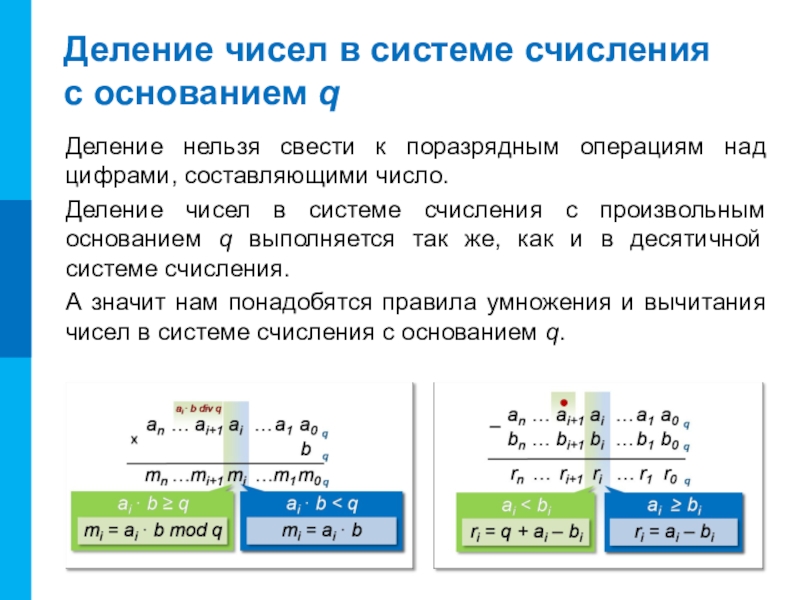
Деление нельзя свести к поразрядным операциям над цифрами, составляющими число.
Деление чисел
А значит нам понадобятся правила умножения и вычитания чисел в системе счисления с основанием q.
Деление чисел в системе счисления
с основанием q
Слайд 17Деление чисел в системе
счисления с основанием q
а)
?
Реши сам
№ 7.
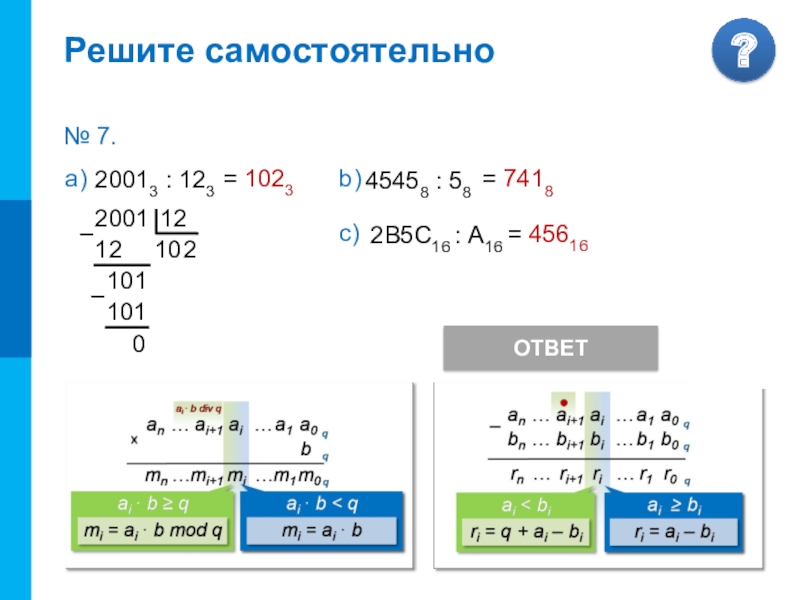
Решите самостоятельно
20013 : 123
1
12
= 1023
101
–
0
2
0
–
1
10
ОТВЕТ
Слайд 19Исходное выражение 24000 + 42016 + 22018 – 8600 + 6
примет вид 24000 + 24032 + 22018 – 21800 + 22 + 21
Вопросы и задания
Задание 1. Найдём количество единиц в двоичной записи числа, являющегося результатом десятичного выражения
24000 + 42016 + 22018 – 8600 + 6.
Решение:
Представим все операнды исходного выражения в виде степеней двойки:
24000 + 42016 + 22018 – 8600 + 6
6 = 4 + 2 = 22 + 21
8600 = (23)600 = 21800
42016 = (22)2016 = 24032
Перепишем выражение в порядке убывания степеней:
24032 + 24000 + 22018 – 21800 + 22 + 21
Слайд 20Вопросы и задания
Для работы с десятичными числами вида 2n полезно иметь
21 = 10 = 1 + 1; 22 = 100 = 11 + 1; 23 = 1000 = 111 + 1; …
24032 + 24000 + 22018 – 21800 + 22 + 21
Эти соотношения позволят подсчитать количество «1» в выраже-нии без вычислений. Двоичные представления чисел 24032 и 24000 внесут в двоичное представление суммы по одной «1». Разность 22018 – 21800 в двоичной записи представляет собой цепочку из 218 единиц и следующих за ними 1800 нулей. Слагаемые 22 и 21 дают ещё 2 единицы. Итого: 1 + 1 + 218 + 1 + 1 = 222.
Решение:
Слайд 21Вопросы и задания
Задание 2. Найдём количество цифр в восьмеричной записи числа,
2299 + 2298 + 2297 + 2296.
Двоичное представление исходного числа имеет вид:
Решение:
Ответ: 100 цифр
Всего в этой записи 300 двоичных символов. При переводе двоичного числа в восьмеричную систему счисления каждая триада исходного числа заменяется восьмеричной цифрой.
Следовательно, восьмеричное представление исходного числа состоит из 100 цифр.
Слайд 22Самое главное
Арифметические операции в позиционных системах счисления с основанием q выполняются
Если необходимо вычислить значение арифметического выражения, операнды которого представлены в различных системах счисления, можно:
все операнды представить в привычной нам десятичной системе счисления;
вычислить результат выражения в десятичной системе счисления;
перевести результат в требуемую систему счисления.
Слайд 23Самое главное
Для работы с десятичными числами вида 2n полезно иметь в
виду
Для натуральных n и m таких, что n > m, получаем:
Слайд 24Вопросы и задания
1. Выполните арифметические операции над двоичными числами. Для того
а) 1011110102 + 1001112
б) 10111,012 + 1,112
в) 101011012 - 111012
г) 110112 · 11012
д) 10110112 : 1112
ОТВЕТ
Слайд 25Вопросы и задания
2. Какое число следует за каждым из данных. Ответ
а) 101112
б) 3445
в) 76778
г) EFF16
Какое число предшествует каждому из данных. Ответ для каждого числа дайте в указанной системе счисления.
ОТВЕТ
ОТВЕТ
Слайд 26Вопросы и задания
3. Сумму восьмеричных чисел
17 + 1 700 +
перевели в 16-теричную систему счисления. Найдите в 16-ной записи числа, равного этой сумме, 5-ю цифру слева.
Найдем сумму данных чисел.
В полученной сумме
10 восьмеричных цифр или
10·3 - 2 = 28 двоичных цифры или
28 : 4 = 7 тетрад
Нас интересует 5-я слева (она же
3-я справа) тетрада: 00112=316
Ответ: цифра 3
Решение:
111
001
111
001
111
00112=316
1
Слайд 27Вопросы и задания
4. Какая первая цифра в шестнадцатеричной записи числа:
2378 +
ОТВЕТ
Ответ: 7
Комментарий.
В двоичной записи числа 379 цифр, первые три из которых «1», остальные – «0», т.е. начало двоичного числа 1110000…
Для перевода в шестнадцатеричную систему счисления двоичное число разделим на тетрады, для этого двоичное число слева дополним одним нулем (01110000…), чтобы получилось ровное число тетрад 380 : 4 = 95.
Первая тетрада (0111) и будет искомой цифрой: 01112=7