- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по информатике Корреляционные зависимости
Содержание
- 1. Презентация по информатике Корреляционные зависимости
- 2. Регрессионная модельэто функция, описывающая зависимость между количественными характеристиками сложных систем.
- 3. Регрессионная модельРегрессионные математические модели строятся в тех
- 4. Еще некоторые задачи регрессииПусть важной характеристикой некоторой
- 5. Модель «ШКОЛА» Пусть
- 6. Итак, пусть хозяйственные расходы школы выражаются количеством
- 7. На рисунке представлены итоги сбора данных по 20 школам
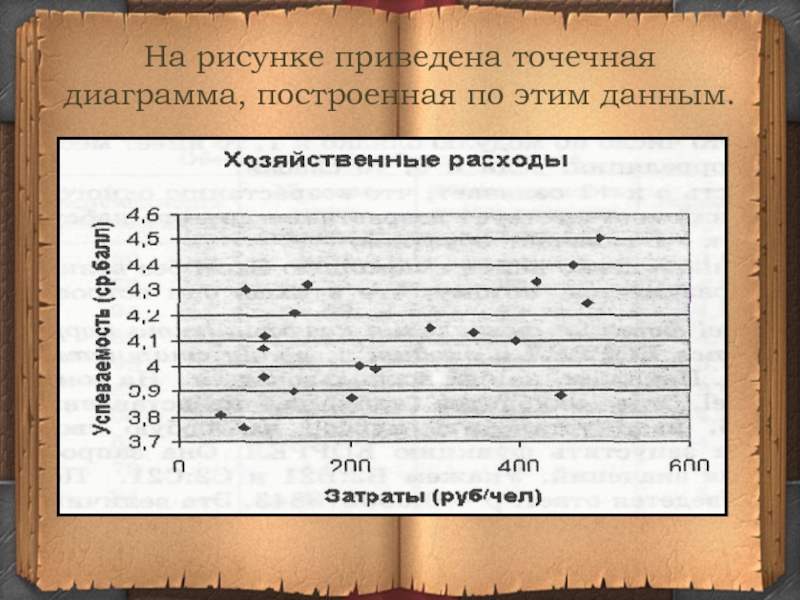
- 8. На рисунке приведена точечная диаграмма, построенная по этим данным.
- 9. Значения обеих величин: финансовых затрат и успеваемости
- 10. Раздел математической статистики, который исследует такие зависимости,
- 11. Коэффициент корреляцииКоэффициент корреляции обозначается греческой буквой ρ
- 12. В Excel функция вычисления коэффициента корреляции называется
- 13. О главном:Зависимости между величинами, каждая из которых
- 14. О главном:Количественной мерой корреляции двух величин является
Регрессионная модельэто функция, описывающая зависимость между количественными характеристиками сложных систем.
Слайд 2Регрессионная модель
это функция, описывающая зависимость между количественными характеристиками сложных систем.
Слайд 3Регрессионная модель
Регрессионные математические модели строятся в тех случаях, когда известно, что
зависимость между двумя факторами существует и требуется получить ее математическое описание.
Слайд 4Еще некоторые задачи регрессии
Пусть важной характеристикой некоторой сложной системы является фактор
А. На него могут оказывать влияние одновременно многие другие факторы: В, С, D и так далее. Мы рассмотрим два типа задач:
1) требуется определить, оказывает ли фактор В какое-либо заметное регулярное влияние на фактор А?
2) Какие из факторов В, С, D и так далее оказывают наибольшее влияние на фактор А?
1) требуется определить, оказывает ли фактор В какое-либо заметное регулярное влияние на фактор А?
2) Какие из факторов В, С, D и так далее оказывают наибольшее влияние на фактор А?
Слайд 5Модель «ШКОЛА»
Пусть
фактор А - средняя
успеваемость учащихся школы,
фактор В — финансовые расходы школы на хозяйственные нужды: ремонт здания, обновление мебели, эстетическое оформление помещения и т. п.
Здесь влияние фактора В на фактор А не очевидно. Наверное, гораздо сильнее на успеваемость влияют другие причины: уровень квалификации учителей, контингент учащихся, уровень технических средств обучения и другие.
фактор В — финансовые расходы школы на хозяйственные нужды: ремонт здания, обновление мебели, эстетическое оформление помещения и т. п.
Здесь влияние фактора В на фактор А не очевидно. Наверное, гораздо сильнее на успеваемость влияют другие причины: уровень квалификации учителей, контингент учащихся, уровень технических средств обучения и другие.
Слайд 6Итак, пусть
хозяйственные расходы школы выражаются количеством рублей, отнесенных к числу
учеников в школе (руб./чел.), потраченных за определенный период времени (например, за последние 5 лет).
Успеваемость же пусть оценивается средним баллом учеников школы по результатам окончания последнего учебного года.
Успеваемость же пусть оценивается средним баллом учеников школы по результатам окончания последнего учебного года.
Слайд 9Значения обеих величин: финансовых затрат и успеваемости учеников имеют значительный разброс
и, на первый взгляд, взаимосвязи между ними не видно.
Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются корреляционными зависимостями.
Мерой корреляционной зависимости является величина, которая называется коэффициентом корреляции.
Зависимости между величинами, каждая из которых подвергается не контролируемому полностью разбросу, называются корреляционными зависимостями.
Мерой корреляционной зависимости является величина, которая называется коэффициентом корреляции.
Слайд 10Раздел математической статистики, который исследует такие зависимости, называется корреляционным анализом.
Корреляционный анализ
изучает усредненный закон поведения каждой из величин в зависимости от значений другой величины, а также меру такой зависимости.
Слайд 11Коэффициент корреляции
Коэффициент корреляции обозначается греческой буквой ρ («ро»).
Это число, заключенное в
диапазоне от -1 до +1 (если это число по модулю близко к 1, то имеет место сильная корреляция, если к 0, то слабая).
Близость ρ к +1 означает, что возрастанию одного набора значений соответствует возрастание другого набора, близость к -1 означает обратное.
Значение ρ легко найти с помощью Excel без всяких формул (разумеется, потому, что в Excel они встроены).
Близость ρ к +1 означает, что возрастанию одного набора значений соответствует возрастание другого набора, близость к -1 означает обратное.
Значение ρ легко найти с помощью Excel без всяких формул (разумеется, потому, что в Excel они встроены).
Слайд 12В Excel функция вычисления коэффициента корреляции называется КОРРЕЛ и входит в
группу статистических функций.
Для её вычисления необходимо:
на том же листе Excel, где находится таблица, надо установить курсор на любую свободную ячейку и запустить функцию КОРРЕЛ.
указать два диапазона значений по которым устанавливается зависимостью
после их ввода выведется ответ. Эта величина говорит о среднем уровне корреляции
Для её вычисления необходимо:
на том же листе Excel, где находится таблица, надо установить курсор на любую свободную ячейку и запустить функцию КОРРЕЛ.
указать два диапазона значений по которым устанавливается зависимостью
после их ввода выведется ответ. Эта величина говорит о среднем уровне корреляции
Слайд 13О главном:
Зависимости между величинами, каждая из которых подвергается не контролируемому полностью
разбросу, называются корреляционными.
С помощью корреляционного анализа можно решить следующие задачи; определить, оказывает ли один фактор существенное влияние на другой фактор; из нескольких факторов выбрать наиболее существенный.
С помощью корреляционного анализа можно решить следующие задачи; определить, оказывает ли один фактор существенное влияние на другой фактор; из нескольких факторов выбрать наиболее существенный.
Слайд 14О главном:
Количественной мерой корреляции двух величин является коэффициент корреляции.
Значение коэффициента корреляции
лежит между -1 и +1. Чем значение ближе по модулю к 1, тем корреляция (связь) сильнее.
В MS Excel для определения коэф-фициента корреляции используется функция КОРРЕЛ из группы статистических данных.
В MS Excel для определения коэф-фициента корреляции используется функция КОРРЕЛ из группы статистических данных.