- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатиричную
Содержание
- 1. Презентация Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатиричную
- 2. Правило №1 Для перевода целого
- 3. Пример 1 А2 = 101111012
- 4. Правило №1.1 Для перевода дробного двоичного
- 5. Пример 2 А2 =
- 6. Правило № 2 Для перевода целого
- 7. Пример 3
- 8. Правило №2.1 Для перевода дробного двоичного
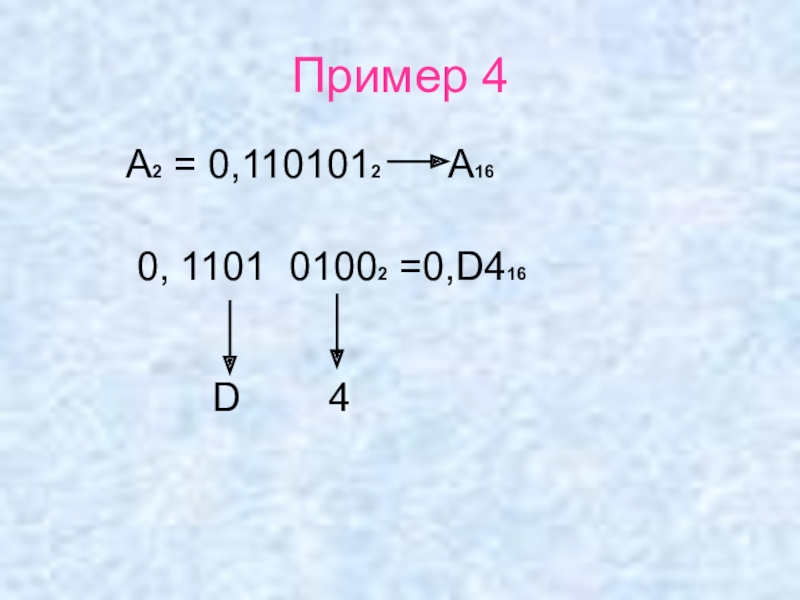
- 9. Пример 4 А2 =
- 10. Правило № 3 Для перевода чисел
- 11. Пример 3А8 = 0,478 А20,
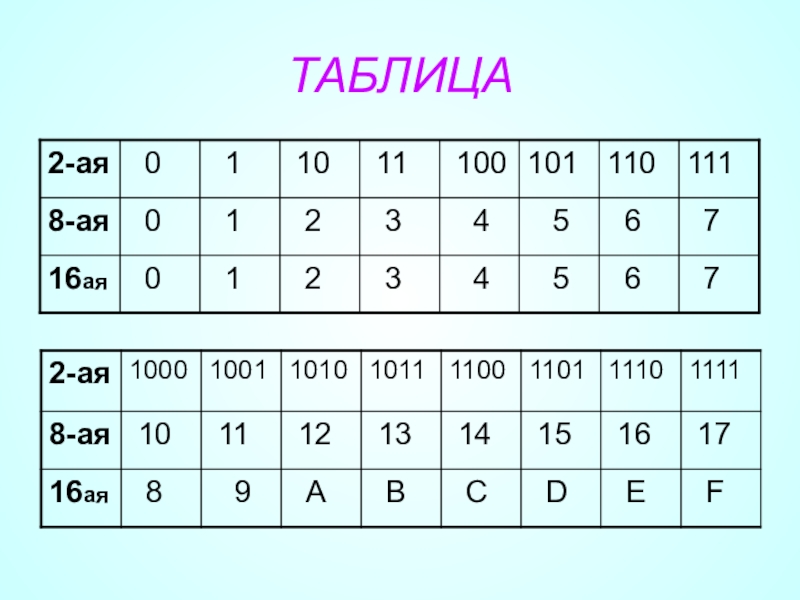
- 12. ТАБЛИЦА
Правило №1 Для перевода целого двоичного числа в восьмеричное его нужно разбить на триады (группы по три цифры), справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой, группе окажется
Слайд 2Правило №1
Для перевода целого двоичного числа в восьмеричное его
нужно разбить на триады (группы по три цифры), справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой, группе окажется меньше трех цифр, то необходимо ее дополнить слева нулями.
Слайд 4Правило №1.1
Для перевода дробного двоичного числа (правильной дроби) в восьмеричное
необходимо разбить его на триады слева направо и, если в последней, правой, группе окажется меньше трех цифр, дополнить ее справа нулями. Далее триады необходимо заменить на восьмеричные числа.
Слайд 6Правило № 2
Для перевода целого двоичного числа в шестнадцатеричное
его нужно разбить на тетрады (группы по четыре цифры), справа налево, и, если в последней, левой, группе окажется меньше четырех цифр, то необходимо ее дополнить слева нулями.
Слайд 8Правило №2.1
Для перевода дробного двоичного числа (правильной дроби) в
шестнадцатеричное необходимо разбить его на тетрады слева направо и, если в последней группе окажется меньше четырех цифр, то необходимо дополнить ее справа нулями.
Слайд 10Правило № 3
Для перевода чисел из восьмеричной и шестнадцатеричной
систем счисления в двоичную необходимо цифры числа преобразовать в группы двоичных цифр. Для перевода из восьмеричной системы счисления в двоичную каждую цифру числа надо преобразовать в группу из трех двоичных цифр (триаду), а при преобразовании шестнадцатеричного числа – в группу из четырех цифр (тетраду).