МБОУ «Средняя общеобразовательная школа №1 г. Медногорска» Оренбургской области
Методическая разработка на тему
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Методическая разработка на тему Использование теории множеств и логики в задачах ЕГЭ по информатике
Содержание
- 1. Методическая разработка на тему Использование теории множеств и логики в задачах ЕГЭ по информатике
- 2. Логика и компьютерДвоичное кодирование – все виды
- 3. МножестваТеория множеств – раздел математики, в котором изучаются
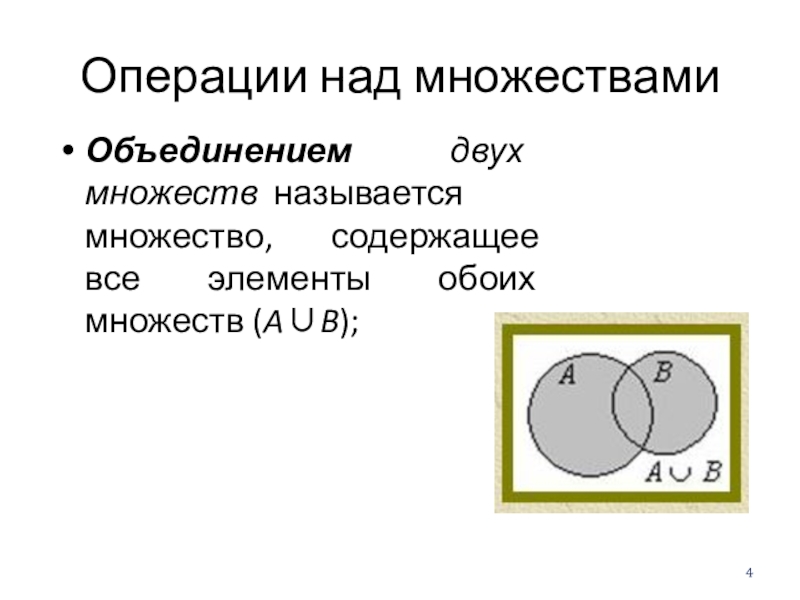
- 4. Операции над множествамиОбъединением двух множеств называется множество, содержащее все элементы обоих множеств (AB);
- 5. Операции над множествамиПересечением двух множеств называется множество, состоящее из общих элементов обоих множеств (AB).
- 6. Операции над множествамиПересечением двух множеств называется множество, состоящее из общих элементов обоих множеств (AB).
- 7. Формула включений и исключенийПусть задано конечное множество
- 8. Принцип включения и исключенияn(AB) = n(A) +
- 9. Принцип включения и
- 10. Операция НЕ (инверсия)Если высказывание A истинно, то
- 11. Операция ИВысказывание «A и B» истинно тогда и только тогда, когда А и B истинны одновременно.
- 12. Операция И (логическое умножение, конъюнкция)10также: A·B, A
- 13. Операция ИЛИ (логическое сложение, дизъюнкция)Высказывание «A или
- 14. Операция ИЛИ (логическое сложение, дизъюнкция)10также: A+B, A
- 15. Операция ИЛИ (логическое сложение, дизъюнкция)10также: A+B, A
- 16. Логические операции
- 17. Логические операцииПорядок выполнения:отрицание;конъюнкция;дизъюнкция;импликация;эквивалентность.
- 18. Законы алгебры логики1 – Истина, 0 - Ложь
- 19. Законы алгебры логикиЗаконы поглощения:A (A
- 20. Операция «исключающее ИЛИ»Высказывание «A B» истинно
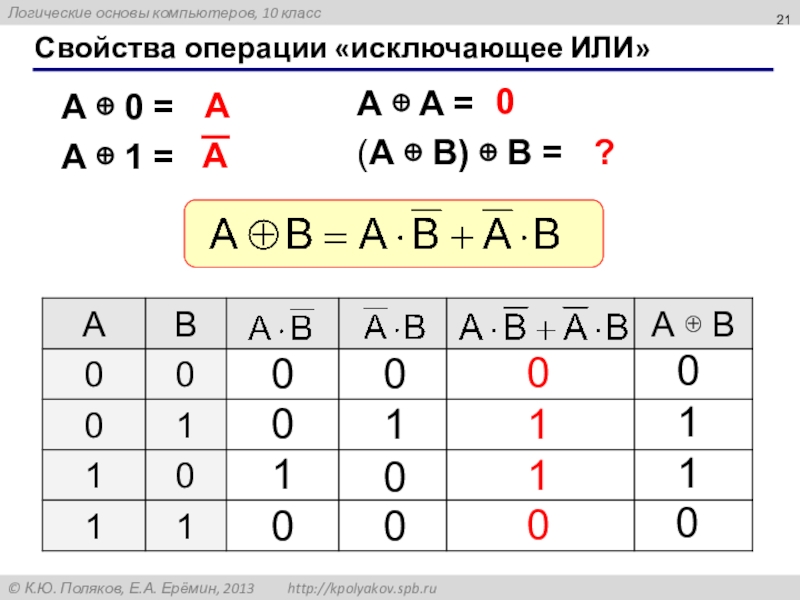
- 21. Свойства операции «исключающее ИЛИ»A A =(A
- 22. Импликация («если …, то …»)Высказывание «A
- 23. Импликация («если …, то …»)«Если Вася идет
- 24. Эквивалентность («тогда и только тогда, …»)Высказывание «A
- 25. Базовый набор операцийС помощью операций И, ИЛИ и НЕ можно реализовать любую логическую операцию.
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. В презентации использованы материалыПОЛЯКОВА Константина Юрьевичаhttp://kpolyakov.spb.ru/index.htm
Слайд 1Использование теории множеств и логики в задачах ЕГЭ по информатике Выполнила учитель информатики
Слайд 2Логика и компьютер
Двоичное кодирование – все виды информации кодируются с помощью
Задача – разработать оптимальные правила обработки таких данных.
Почему «логика»?
Результат выполнения операции можно представить как истинность (1) или ложность (0) некоторого высказывания.
Джордж Буль разработал основы алгебры, в которой используются только 0 и 1 (алгебра логики, булева алгебра).
Слайд 3Множества
Теория множеств – раздел математики, в котором изучаются общие свойства множеств — совокупностей элементов
a∈A; bA;
A={1, 2, 7, 9, 4};
A={xN: x<15};
Множество B называется подмножеством множества A, если все его элементы содержатся в A (BA)
Слайд 4Операции над множествами
Объединением двух множеств называется множество, содержащее все элементы обоих множеств
Слайд 5Операции над множествами
Пересечением двух множеств называется множество, состоящее из общих элементов обоих
Слайд 6Операции над множествами
Пересечением двух множеств называется множество, состоящее из общих элементов обоих
Слайд 7Формула включений и исключений
Пусть задано конечное множество А. Число его элементов
n(А ∪ В) = n(А) + n(В) – n(А ∩ В) (1)
С помощью формулы (1) можно получить формулы для определения числа элементов суммы любого числа множеств.
Например,
n(А ∪ В ∪ С) = n(А ∪ (В ∪ С)) = n(А) + n(В ∪ С) – n(А ∩ (В ∪ С)) =
= n(А) + n(В) + n(С) – n(В ∩ С) – n((А ∩ В) ∪ (А ∩ С)) =
= n(А) + n(В) + n(С) – n(В ∩ С) – (n(А ∩ В) + n(А ∩ С) – n((А ∩ В) ∩ (А ∩ С))) =
=n(А) + n(В) + n(С) – n(В ∩ С) – n(А ∩ В) – n(А ∩ C) + n(А ∩ В ∩ С).
n(А ∪ В ∪ С) = n(А) + n(В) + n(С) – n(А ∩ В) – n(В ∩ С) – n(А ∩ C) + n(А ∩ В ∩ С) (2)
Формулы (1) и (2) называют формулами включений и исключений.
Слайд 8Принцип включения и исключения
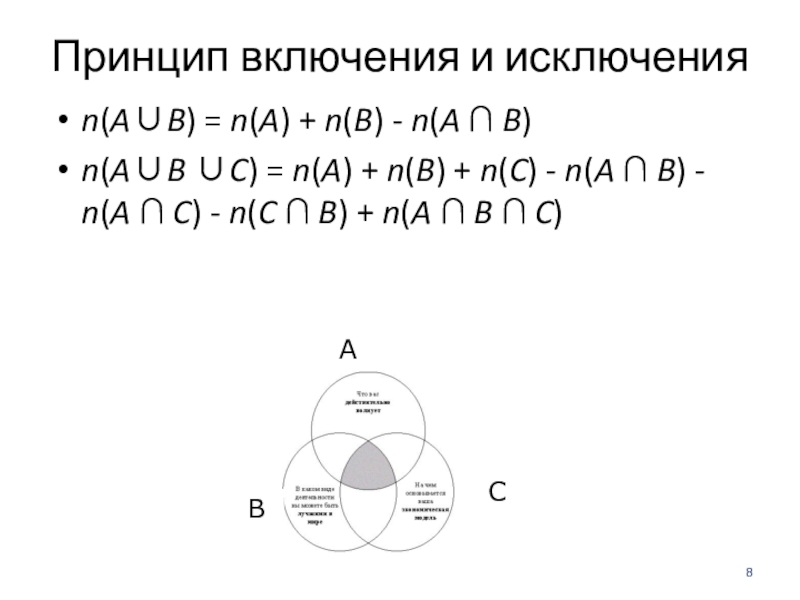
n(AB) = n(A) + n(B) - n(A
n(AB C) = n(A) + n(B) + n(C) - n(A B) - n(A C) - n(C B) + n(A B C)
A
B
C
Слайд 9
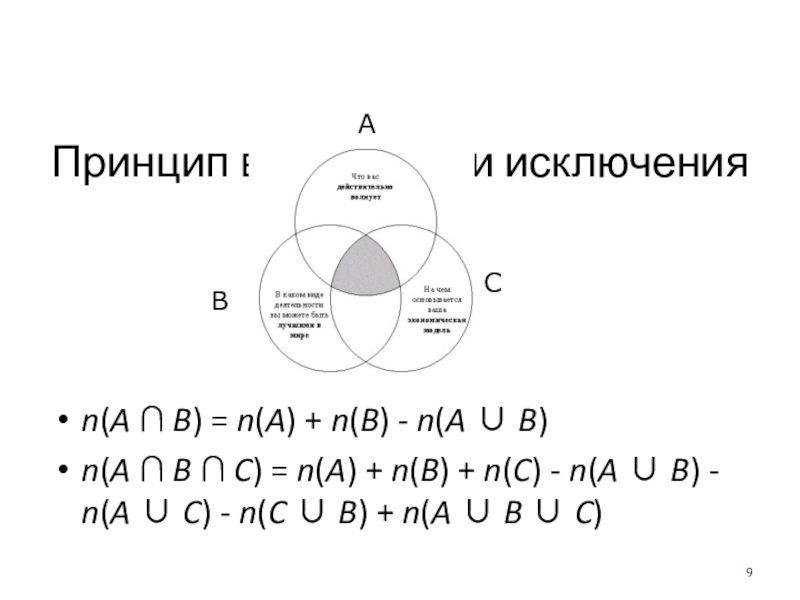
Принцип включения и исключения
n(A B) = n(A) + n(B) -
n(A B C) = n(A) + n(B) + n(C) - n(A B) - n(A C) - n(C B) + n(A B C)
A
B
C
Слайд 10Операция НЕ (инверсия)
Если высказывание A истинно, то «не А» ложно, и
1
0
0
1
таблица истинности операции НЕ
также , ,
not A (Паскаль),
! A (Си)
Таблица истинности логического выражения Х – это таблица, где в левой части записываются все возможные комбинации значений исходных данных, а в правой – значение выражения Х для каждой комбинации.
Слайд 11Операция И
Высказывание «A и B» истинно тогда и только тогда, когда
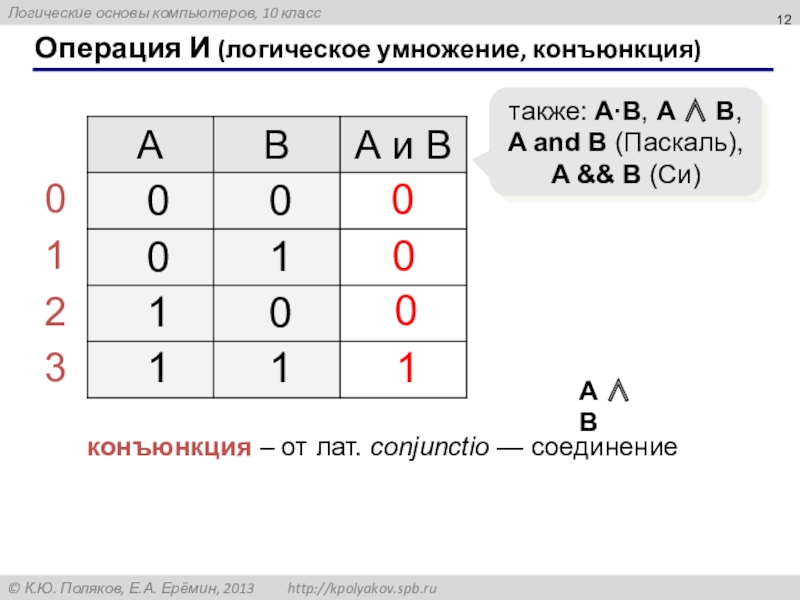
Слайд 12Операция И (логическое умножение, конъюнкция)
1
0
также: A·B, A B,
A and B
0
0
конъюнкция – от лат. conjunctio — соединение
A B
Слайд 13Операция ИЛИ (логическое сложение, дизъюнкция)
Высказывание «A или B» истинно тогда, когда
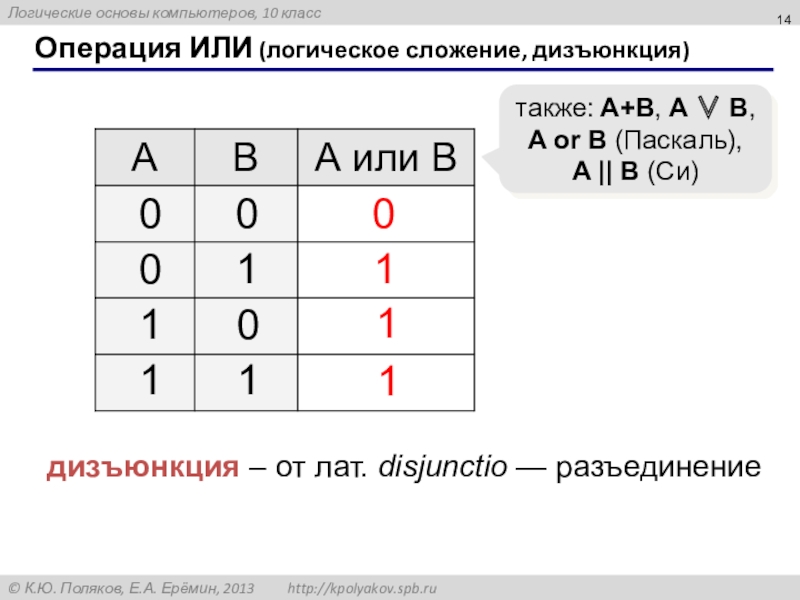
Слайд 14Операция ИЛИ (логическое сложение, дизъюнкция)
1
0
также: A+B, A B,
A or B
1
1
дизъюнкция – от лат. disjunctio — разъединение
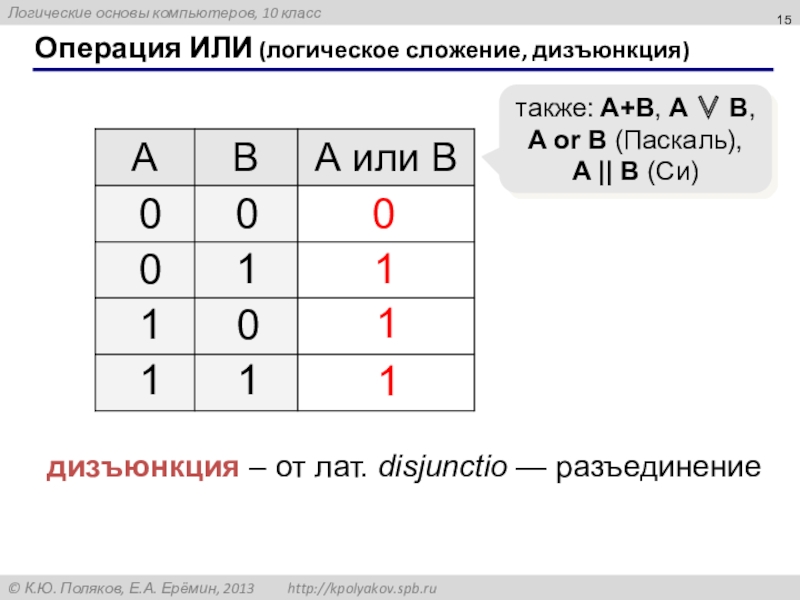
Слайд 15Операция ИЛИ (логическое сложение, дизъюнкция)
1
0
также: A+B, A B,
A or B
1
1
дизъюнкция – от лат. disjunctio — разъединение
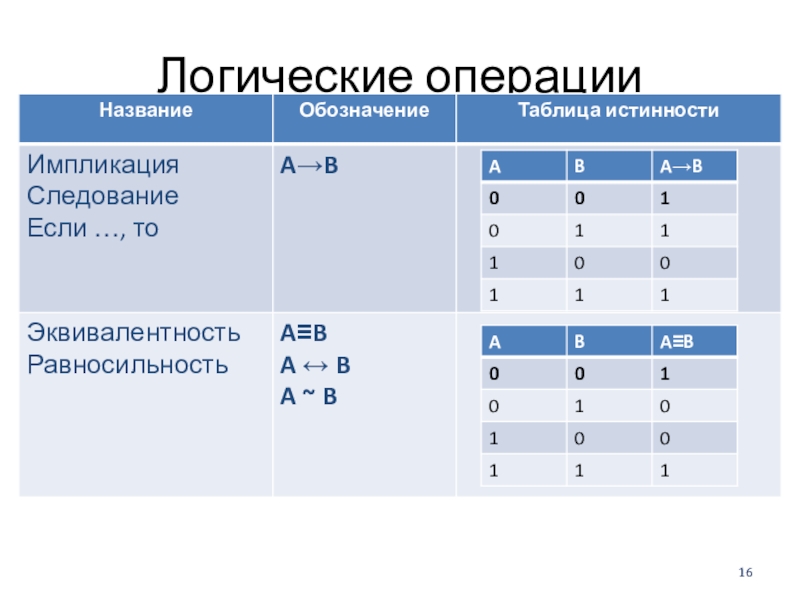
Слайд 17Логические операции
Порядок выполнения:
отрицание;
конъюнкция;
дизъюнкция;
импликация;
эквивалентность.
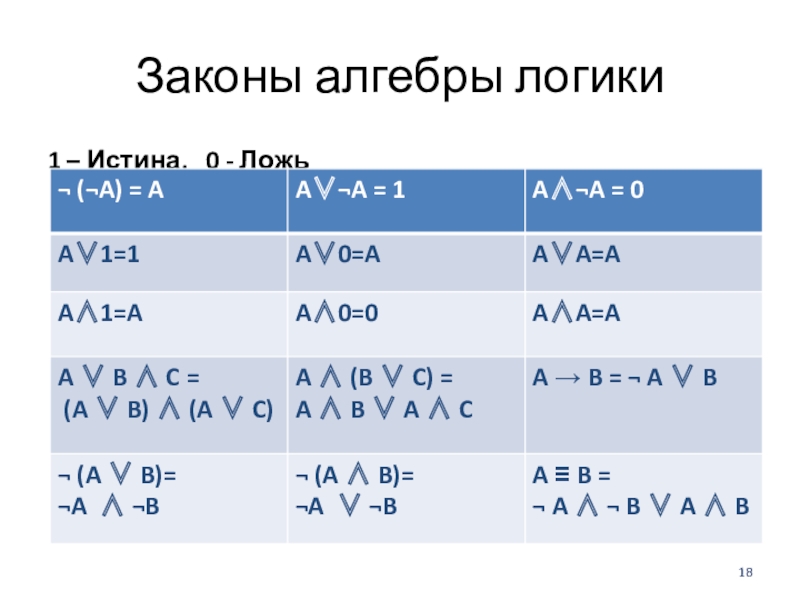
Слайд 19Законы алгебры логики
Законы поглощения:
A (A B) = A
¬A
A (A B) = A
¬A (A B) = ¬A B
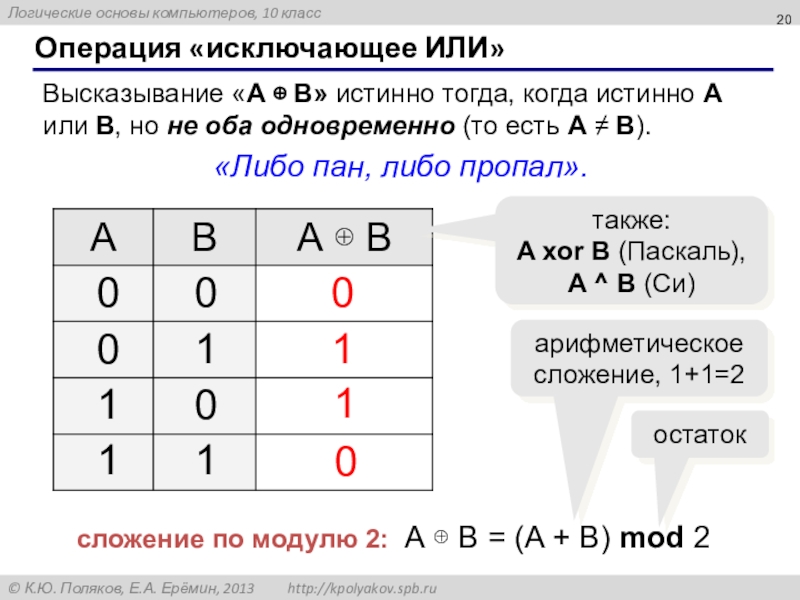
Слайд 20Операция «исключающее ИЛИ»
Высказывание «A B» истинно тогда, когда истинно А
«Либо пан, либо пропал».
0
0
также:
A xor B (Паскаль),
A ^ B (Си)
1
1
сложение по модулю 2: А B = (A + B) mod 2
арифметическое сложение, 1+1=2
остаток
Слайд 22Импликация («если …, то …»)
Высказывание «A B» истинно, если не
A – «Работник хорошо работает».
B – «У работника хорошая зарплата».
1
1
1
0
Слайд 23Импликация («если …, то …»)
«Если Вася идет гулять, то Маша сидит
A – «Вася идет гулять».
B – «Маша сидит дома».
Маша может пойти гулять (B=0), а может и не пойти (B=1)!