- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Информатика 8 класс. Перевод из любой системы счисления в десятичную
Содержание
- 1. Информатика 8 класс. Перевод из любой системы счисления в десятичную
- 2. ВопросыСистема счисления – это…Отличие позиционной и непозиционных
- 3. Проверка знаний1. Представьте числа в развернутом виде.
- 4. 2. Представьте число в свернутом виде и
- 5. Дополнительное задание1) 4·5–1 + 35–2 + 2·3–3
- 6. Перевод целых чисел в 2, 8, 16-ую системы счисления 0123456789ABCDEF01234567890123456701шестнадцатеричнаядесятичнаядвоичнаявосьмеричная
- 7. Алгоритм перевода десятичных чисел в двоичную систему
- 8. Примеры перевода чисел:Пример1 Пример2 Пример31310 → ?2 12610 → ?8 18010 → ?161310 = 11012 12610 = 1768 18010 = В416
- 9. Перевод целого числа из десятичной системы счисления
- 10. Перевод целого числа из десятичной системы счисления
- 11. Перевод целого числа из десятичной системы счисления
- 12. ЗаданиеПеревести целое десятичное число в указанную систему:9610 -
- 13. Самостоятельно7810 - ?2 8710 - ?2 12310 - ?8 13210 - ?8 41210 - ?16 42110 - ?16
- 14. Домашнее заданиеПеревести в двоичную систему и сложить:17810 и 18710 24310 и 32710Перевести в двоичную систему и перемножить:1810 и 1710
ВопросыСистема счисления – это…Отличие позиционной и непозиционных систем счисленияПримеры непозиционных систем счисления, их недостаткиЧто такое «основание позиционной системы счисления»Развернутая запись числа – это сумма…Алгоритм перевода из десятичной в двоичную
Слайд 2Вопросы
Система счисления – это…
Отличие позиционной и непозиционных систем счисления
Примеры непозиционных систем
счисления, их недостатки
Что такое «основание позиционной системы счисления»
Развернутая запись числа – это сумма…
Алгоритм перевода из десятичной в двоичную
Что такое «основание позиционной системы счисления»
Развернутая запись числа – это сумма…
Алгоритм перевода из десятичной в двоичную
Слайд 3Проверка знаний
1. Представьте числа в развернутом виде.
1) 1845,2310 = _____________
2)
1845,238 = _____________
3) 1010,0112 = _____________
4) 122,АА16 = _____________
3) 1010,0112 = _____________
4) 122,АА16 = _____________
Слайд 42. Представьте число в свернутом виде и определите, чему оно соответствует
в десятичной системе счисления.
1) 1·25 + 0·24 + 0·23 + 1·22 + 1·21 + 0·20 + 1·2–1 + 1·2–2 = ____________2 = _________10
2) 1·35 + 0·34 + 2·33 + 1·32 + 0·31 + 1·20 + 2·3–1 + 0·3–2 + 1·3–3 = ____________3 = =_________10
1) 1·25 + 0·24 + 0·23 + 1·22 + 1·21 + 0·20 + 1·2–1 + 1·2–2 = ____________2 = _________10
2) 1·35 + 0·34 + 2·33 + 1·32 + 0·31 + 1·20 + 2·3–1 + 0·3–2 + 1·3–3 = ____________3 = =_________10
Слайд 5Дополнительное задание
1) 4·5–1 + 35–2 + 2·3–3 = _____5 = ______10
2)
1·83 + 2·81 + 5·80 + 7·8–1 + 1·3–2 = _______8 = _________10
3) А·162 + В·161 + F·160 + C·16–1 = ____________3 =______10
3) А·162 + В·161 + F·160 + C·16–1 = ____________3 =______10
Слайд 6
Перевод целых чисел в 2, 8, 16-ую системы счисления
0123456789ABCDEF
0123456789
01234567
01
шестнадцатеричная
десятичная
двоичная
восьмеричная
Слайд 7Алгоритм перевода десятичных чисел в двоичную систему счисления:
Разделить число на 2.
Зафиксировать остаток (0 или 1) и частное.
Если частное не равно 0, то разделить его на 2, и так далее пока частное не станет равно 0. Если частное равно 0 , то записать все полученные остатки, начиная с первого, справа налево.
Если частное не равно 0, то разделить его на 2, и так далее пока частное не станет равно 0. Если частное равно 0 , то записать все полученные остатки, начиная с первого, справа налево.
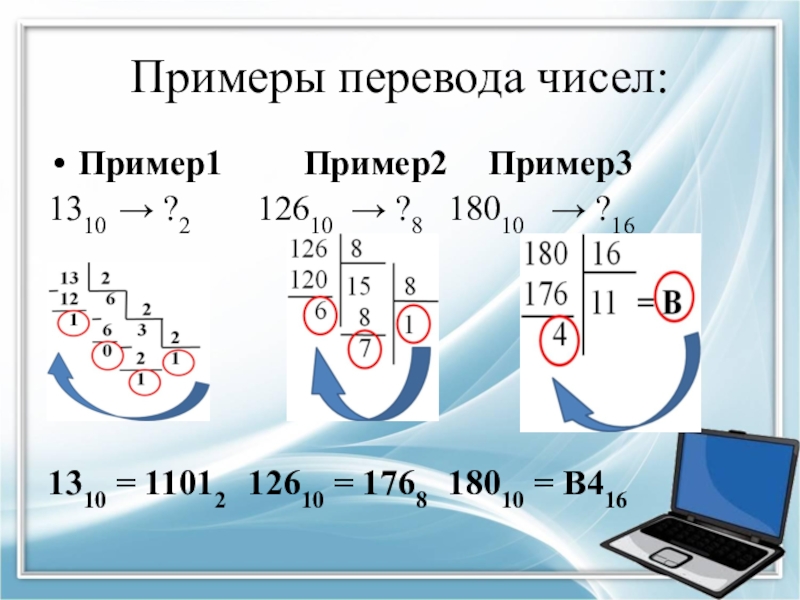
Слайд 8Примеры перевода чисел:
Пример1 Пример2 Пример3
1310 → ?2 12610 → ?8 18010 → ?16
1310 = 11012 12610 = 1768 18010 = В416
Слайд 9Перевод целого числа из десятичной системы счисления в произвольную.
1. Последовательно выполнять
деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, меньше делителя.
2. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
3. Составить число в новой системе счисления, записывая его, начиная с последнего остатка.
2. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
3. Составить число в новой системе счисления, записывая его, начиная с последнего остатка.
Слайд 10Перевод целого числа из десятичной системы счисления в произвольную.
2 способ
Последовательно представлять
число в виде суммы произведения степеней основания на цифру, не превышающую максимально возможную в данном основании
Пример (перевести число в двоичную сс):
9310=
Пример (перевести число в двоичную сс):
9310=
Слайд 11Перевод целого числа из десятичной системы счисления в произвольную.
2 способ
Последовательно представлять
число в виде суммы произведения степеней основания на цифру, не превышающую максимально возможную в данном основании
Пример (перевести число в двоичную сс):
9310=64+29=64+16+13=64+16+8+5=
=64+16+8+4+1=1*26+1*24+1*23+1*22+1*20
=10111012
Пример (перевести число в двоичную сс):
9310=64+29=64+16+13=64+16+8+5=
=64+16+8+4+1=1*26+1*24+1*23+1*22+1*20
=10111012
Слайд 12Задание
Перевести целое десятичное число в указанную систему:
9610 - ?2 45910 - ?2
12010 - ?8 21110 - ?8
45710 - ?16
Слайд 14Домашнее задание
Перевести в двоичную систему и сложить:
17810 и 18710 24310 и 32710
Перевести в двоичную
систему и перемножить:
1810 и 1710
1810 и 1710