логические элементы.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Элементы математической логики. Основные логические элементы.
Содержание
- 1. Элементы математической логики. Основные логические элементы.
- 2. I. Общие сведения о науке «Логика»Логика –
- 3. Математическая логика является одной из частей формальной
- 4. В алгебре логики рассматриваются логические операцииЛогическое отрицание
- 5. Логическое отрицание «Инверсия» Добавление к высказыванию связки
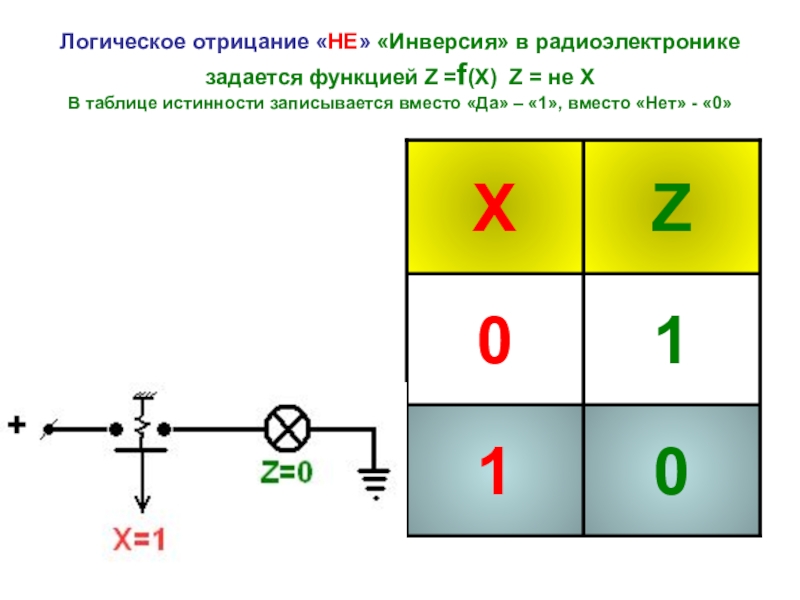
- 6. Логическое отрицание «НЕ» «Инверсия» в радиоэлектронике задается
- 7. Логическое отрицание «НЕ» «Инверсия» в радиоэлектронике задается
- 8. Логическое отрицание «НЕ» «Инверсия» в радиоэлектронике задается
- 9. Логическое отрицание «НЕ» «Инверсия» в радиоэлектронике задается
- 10. Логическое отрицание «НЕ» «Инверсия» в радиоэлектронике задается
- 11. Логическое отрицание «НЕ» «Инверсия» в радиоэлектронике задается
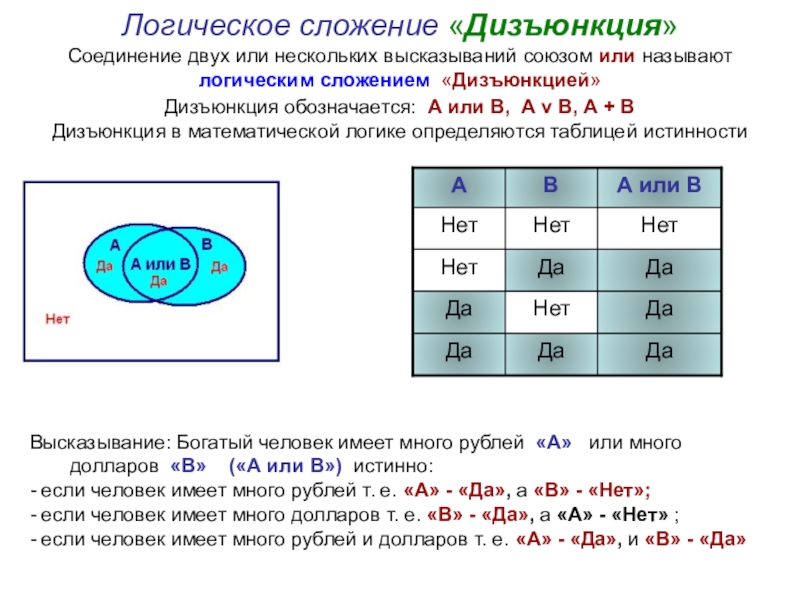
- 12. Логическое сложение «Дизъюнкция» Соединение двух или нескольких
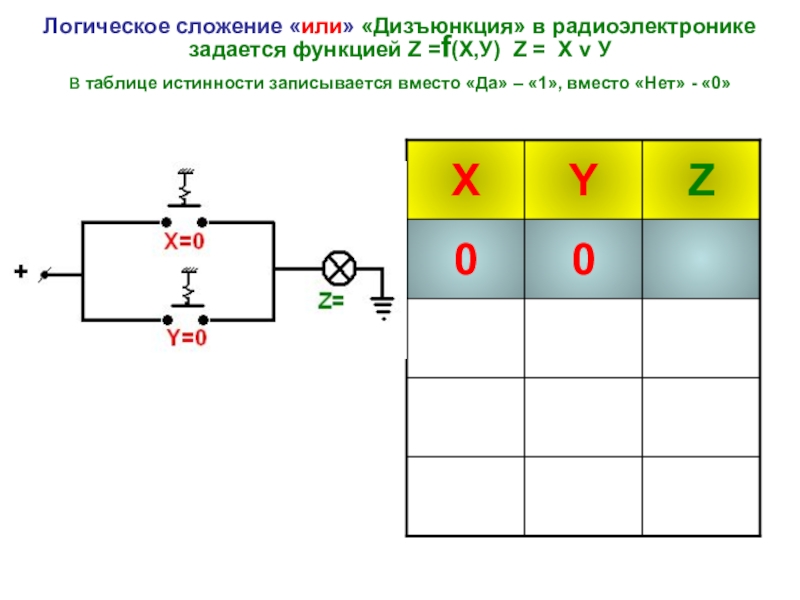
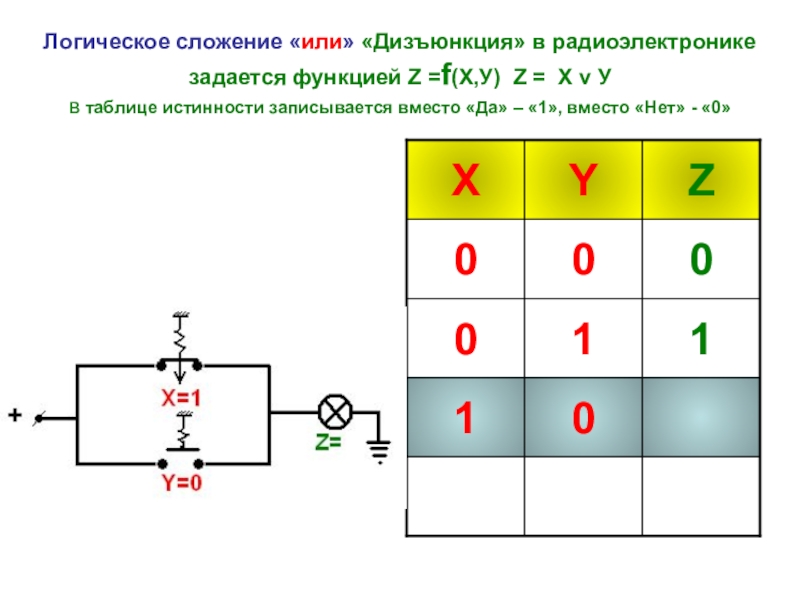
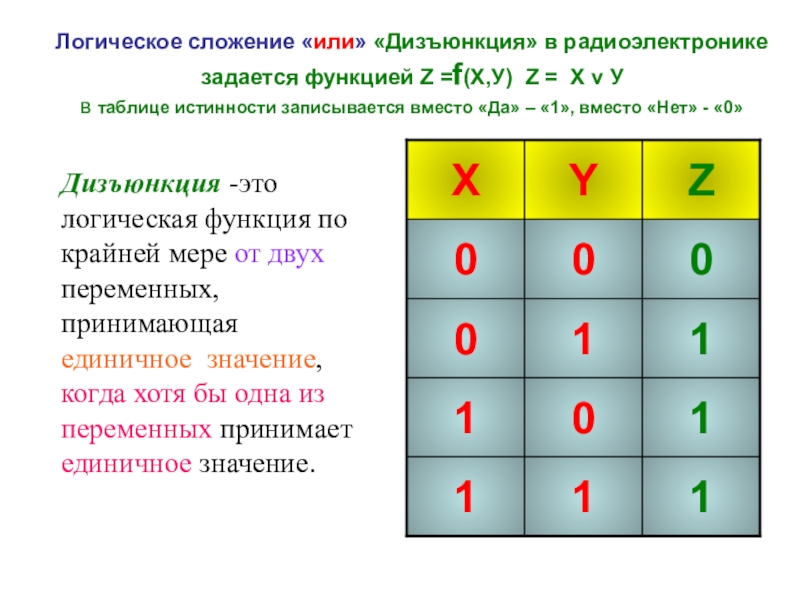
- 13. Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается
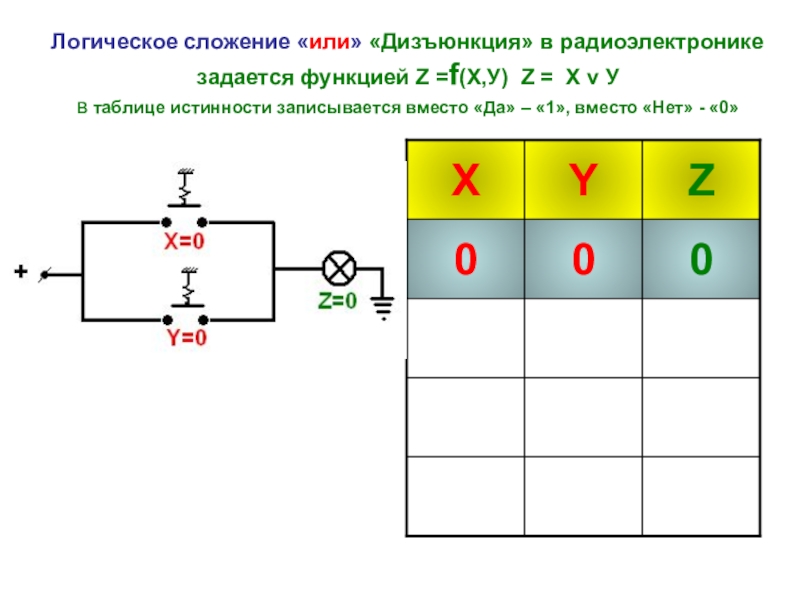
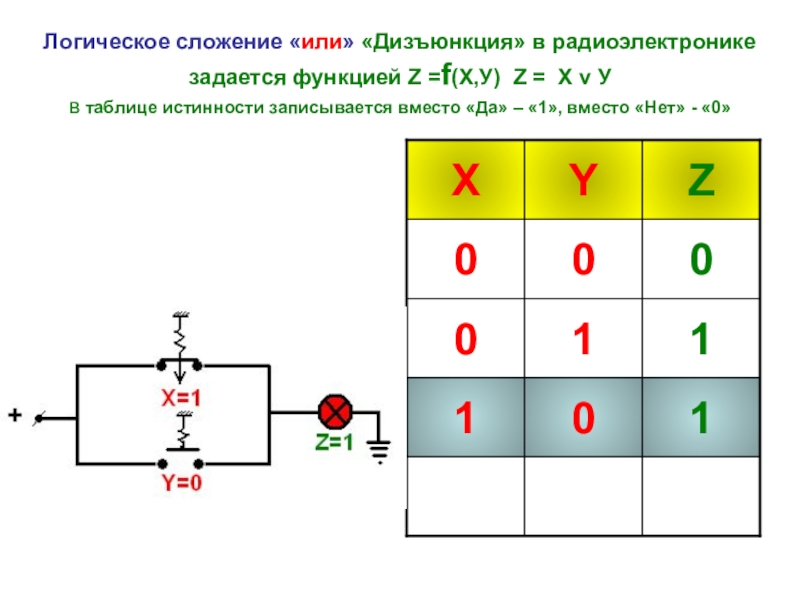
- 14. Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается
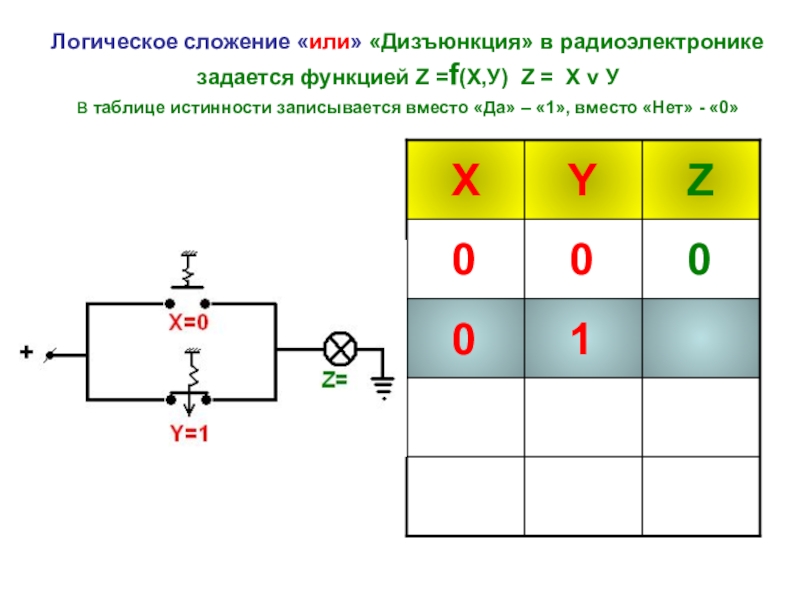
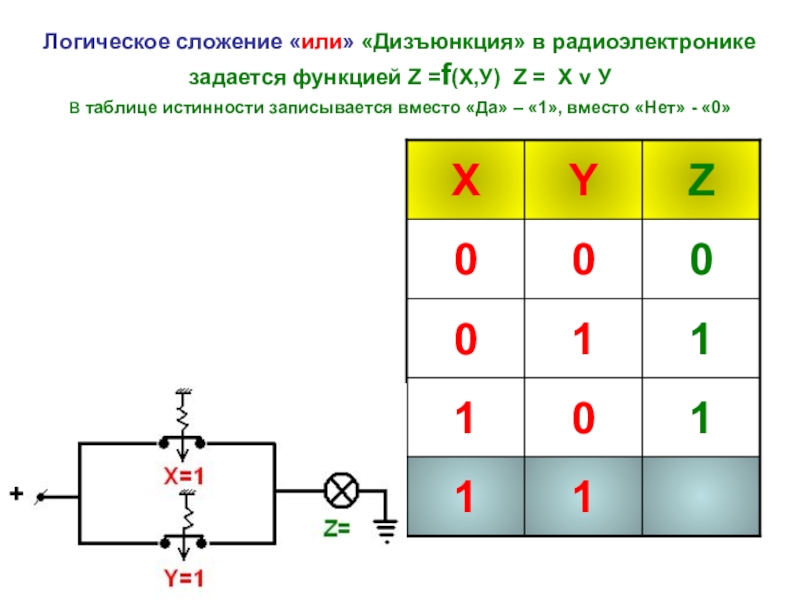
- 15. Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается
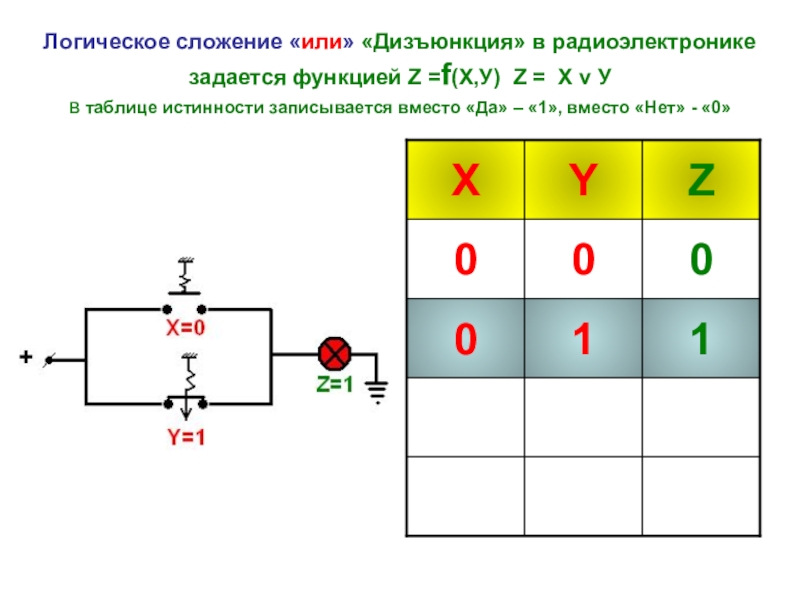
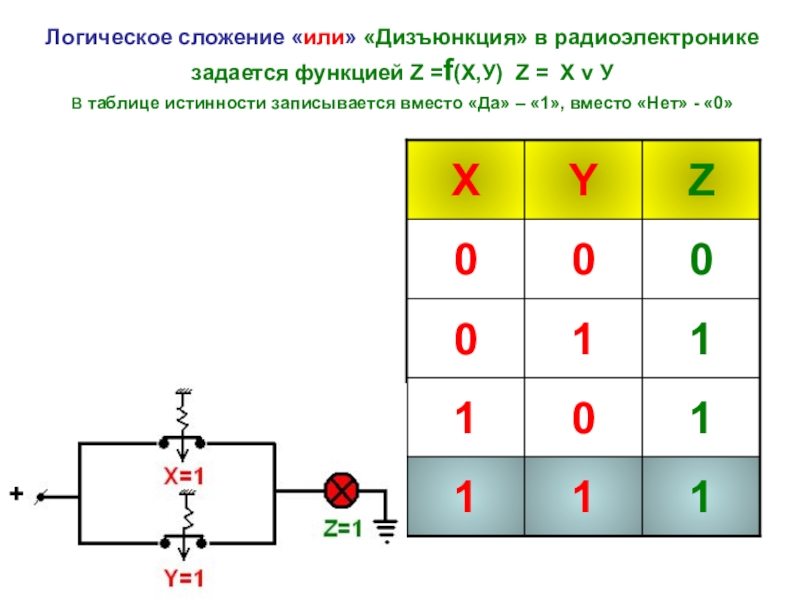
- 16. Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается
- 17. Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается
- 18. Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается
- 19. Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается
- 20. Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается
- 21. Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается
- 22. Логическое элемент «Дизъюнктор» (элемент «ИЛИ»)
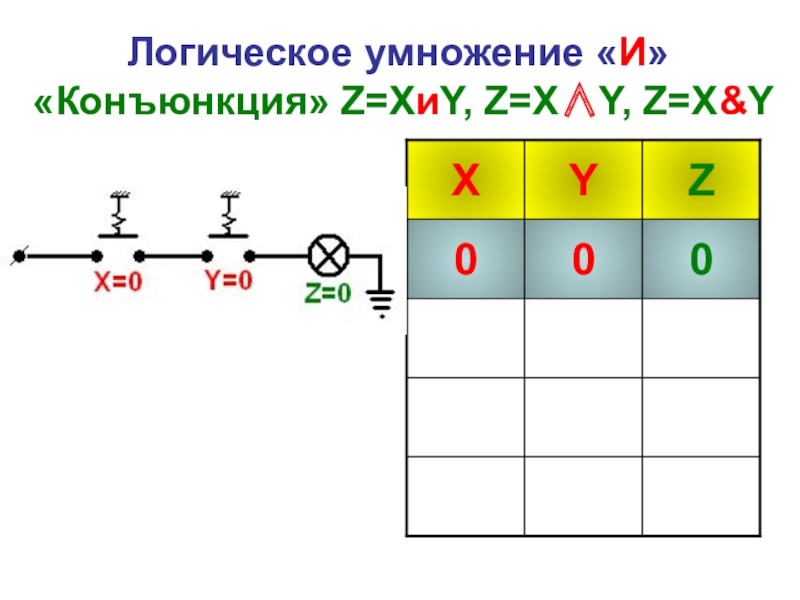
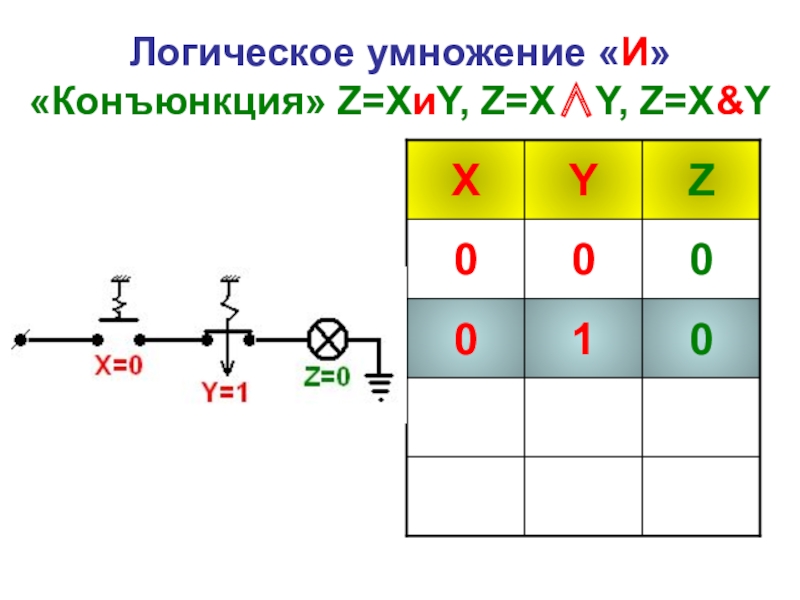
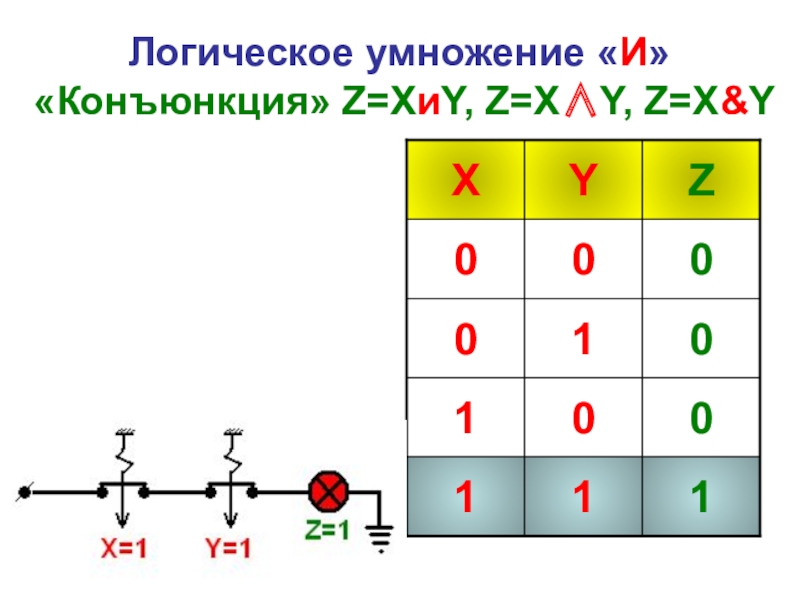
- 23. Логическое умножение «И» «Конъюнкция» Z=XиY, Z=X∧Y, Z=X&Y
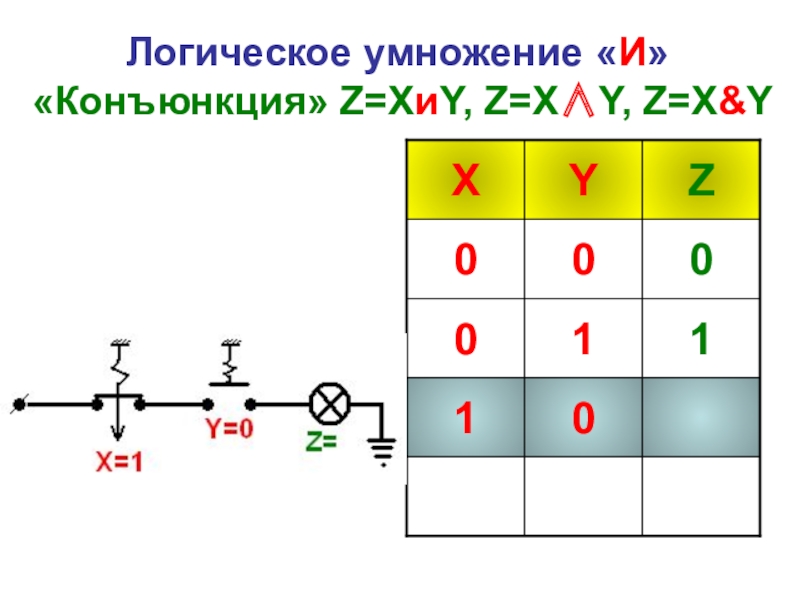
- 24. Логическое умножение «И» «Конъюнкция» Z=XиY, Z=X∧Y, Z=X&Y
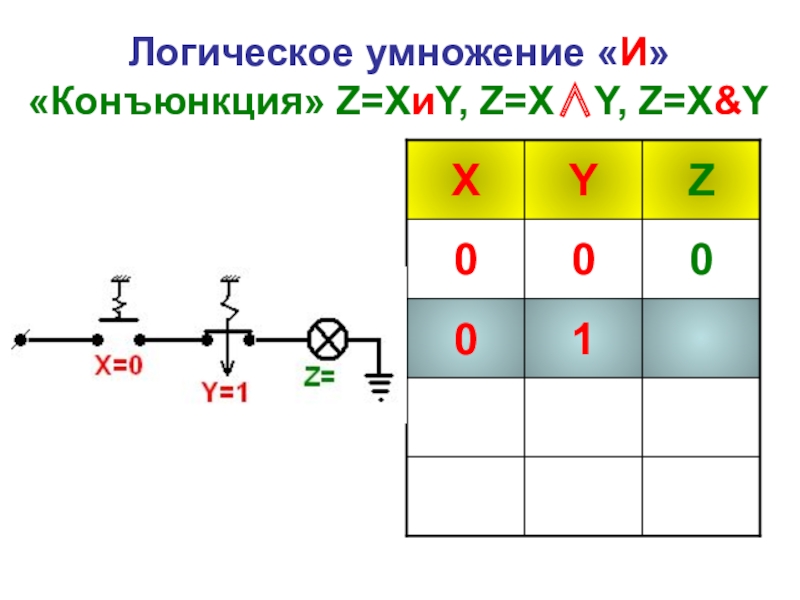
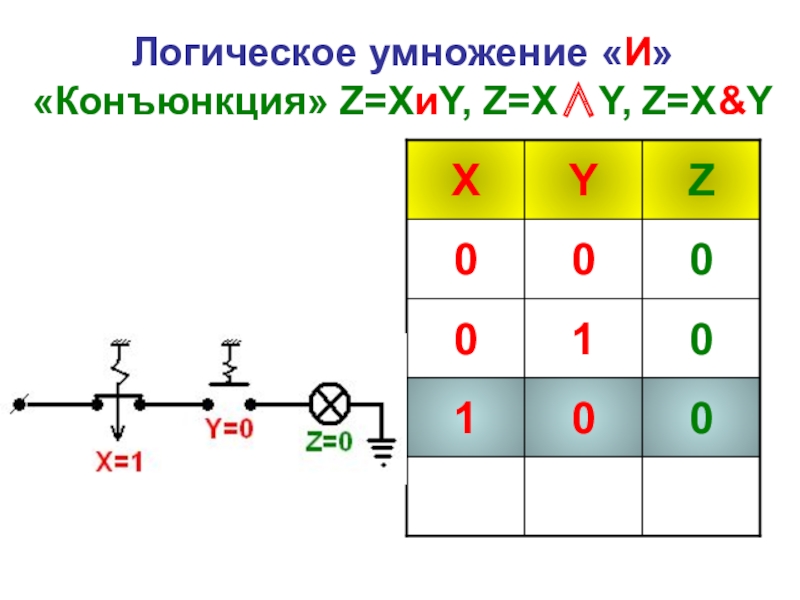
- 25. Логическое умножение «И» «Конъюнкция» Z=XиY, Z=X∧Y, Z=X&Y
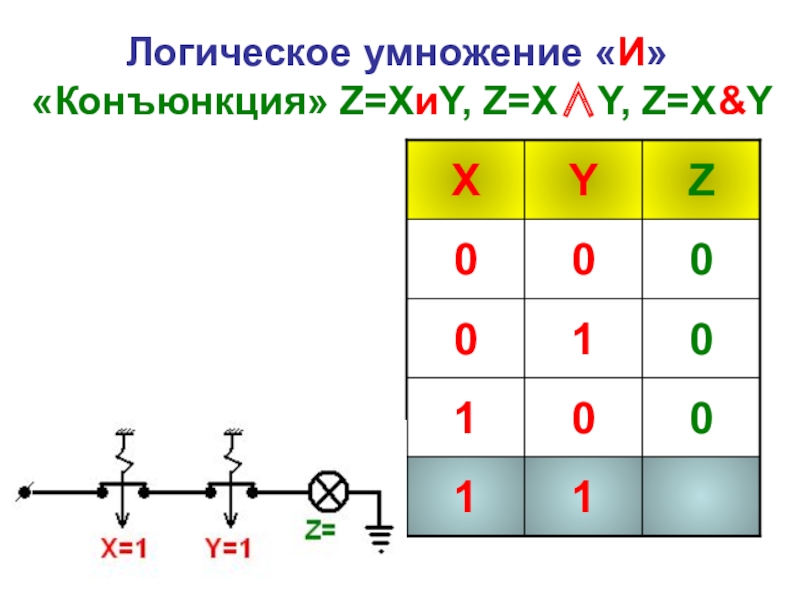
- 26. Логическое умножение «И» «Конъюнкция» Z=XиY, Z=X∧Y, Z=X&Y
- 27. Логическое умножение «И» «Конъюнкция» Z=XиY, Z=X∧Y, Z=X&Y
- 28. Логическое умножение «И» «Конъюнкция» Z=XиY, Z=X∧Y, Z=X&Y
- 29. Логическое умножение «И» «Конъюнкция» Z=XиY, Z=X∧Y, Z=X&Y
- 30. Логическое умножение «И» «Конъюнкция» Z=XиY, Z=X∧Y, Z=X&Y
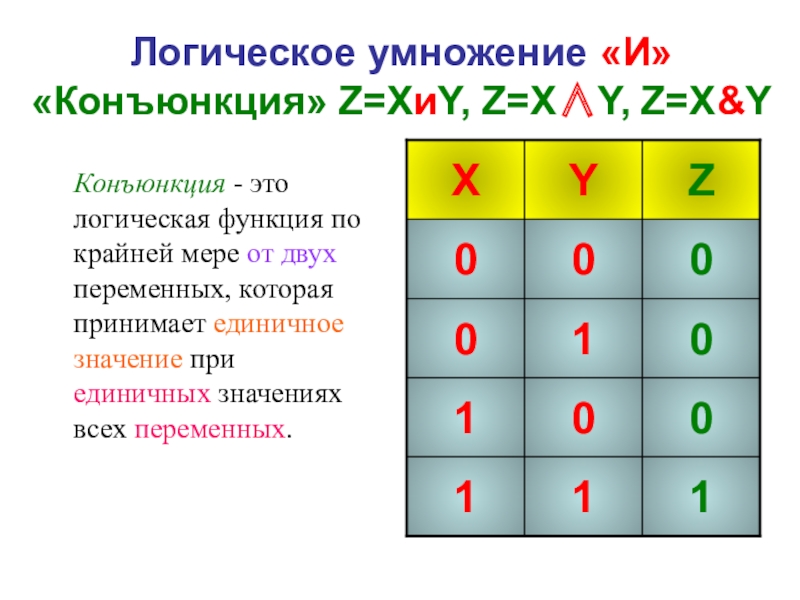
- 31. Логическое умножение «И» «Конъюнкция» Z=XиY, Z=X∧Y, Z=X&YКонъюнкция
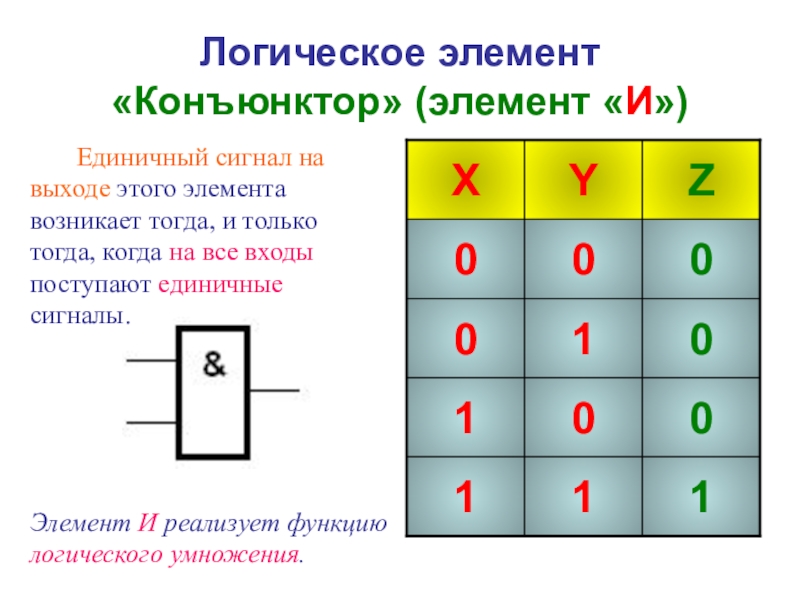
- 32. Логическое элемент «Конъюнктор» (элемент «И»)
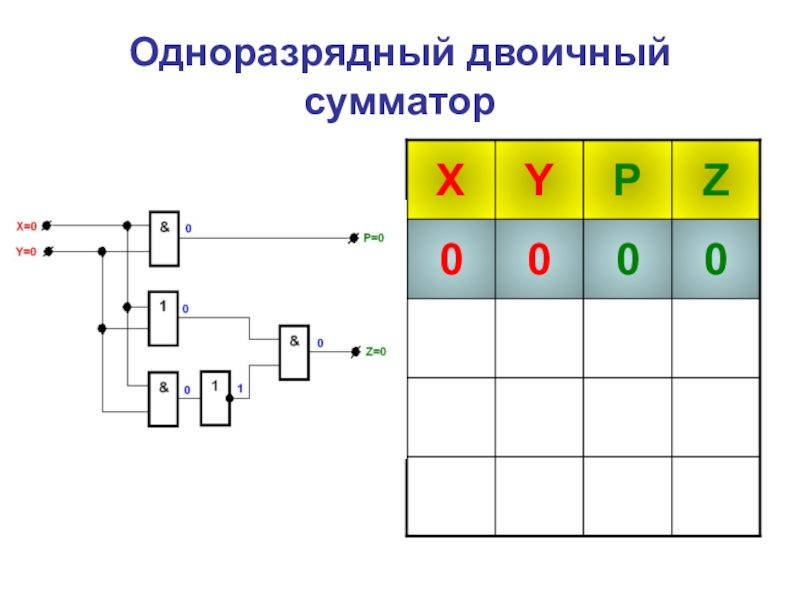
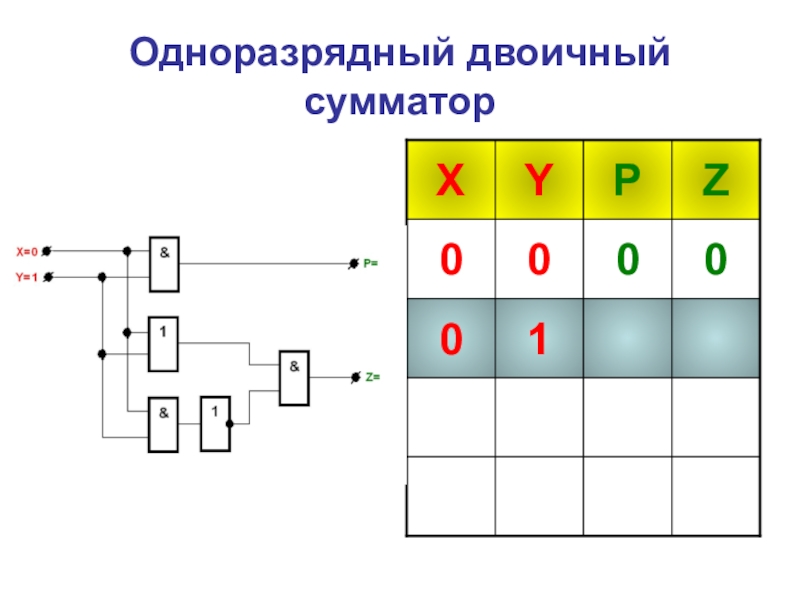
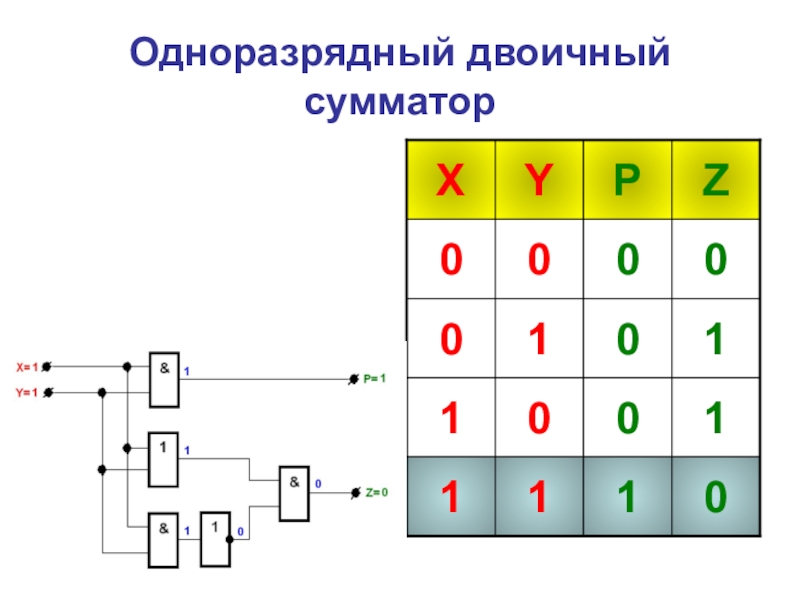
- 33. Одноразрядный двоичный сумматор
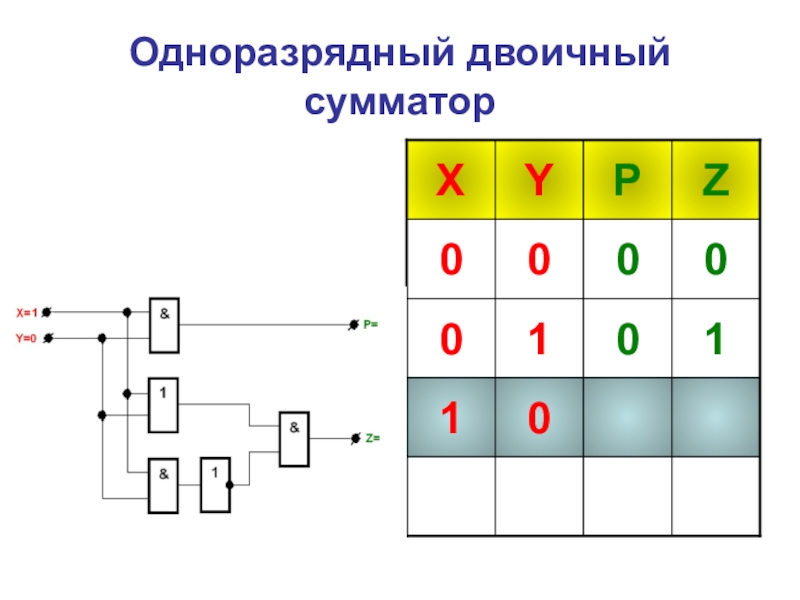
- 34. Одноразрядный двоичный сумматор
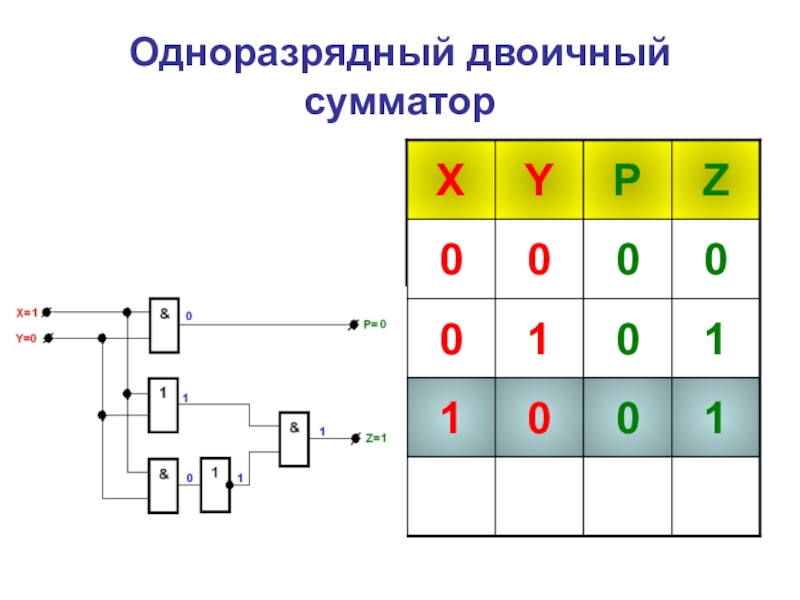
- 35. Одноразрядный двоичный сумматор
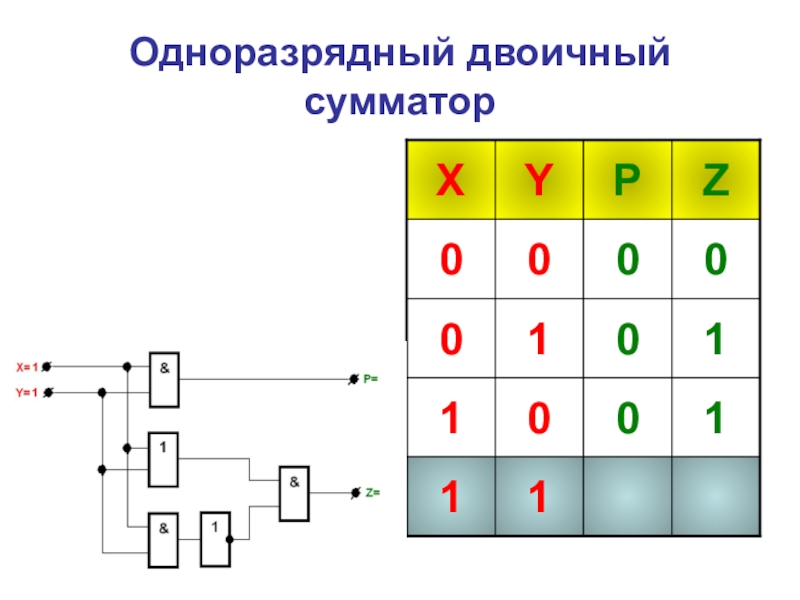
- 36. Одноразрядный двоичный сумматор
- 37. Одноразрядный двоичный сумматор
- 38. Одноразрядный двоичный сумматор
- 39. Одноразрядный двоичный сумматор
- 40. Одноразрядный двоичный сумматор
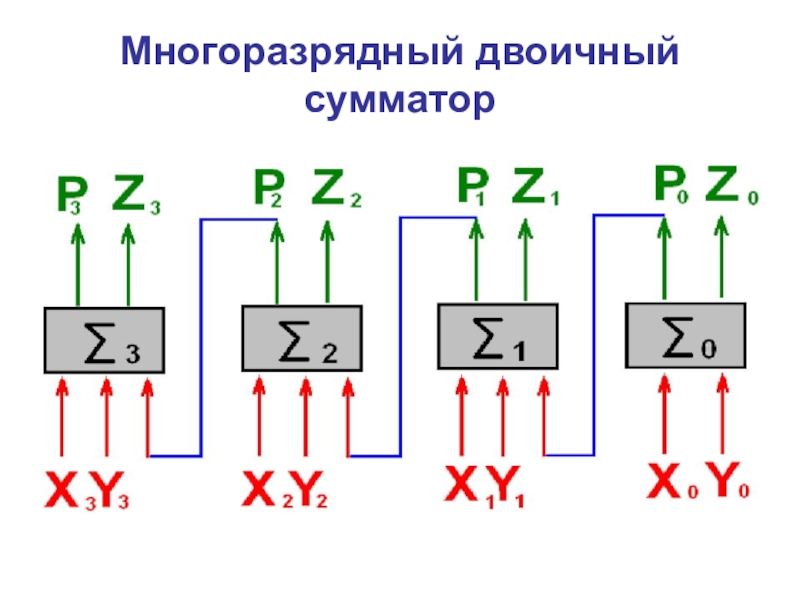
- 41. Многоразрядный двоичный сумматор
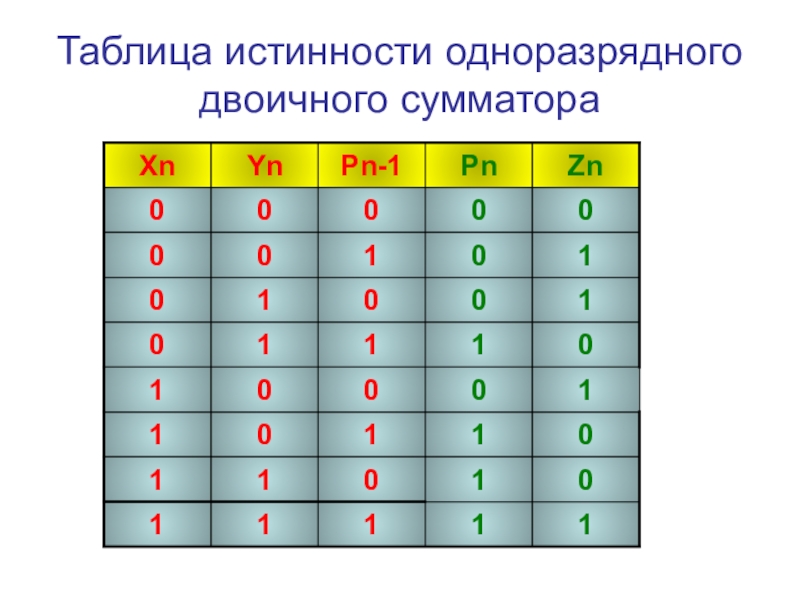
- 42. Таблица истинности одноразрядного двоичного сумматора
I. Общие сведения о науке «Логика»Логика – это наука о формах и способах мышления.Понятие – форма мышления фиксирующая основные, существенные признаки объекта.Высказывание – это форма мышления, в которой что – либо утверждается или отрицается о реальных
Слайд 2I. Общие сведения о науке «Логика»
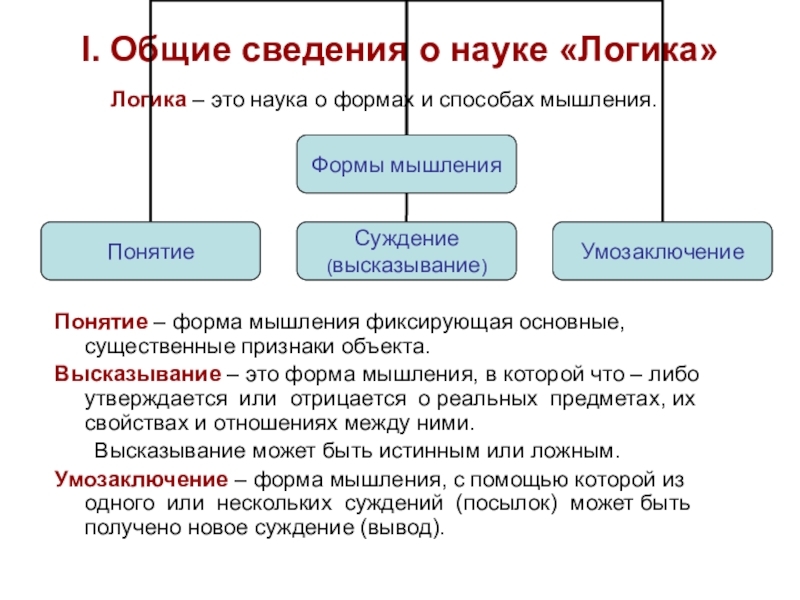
Логика – это наука о формах
и способах мышления.
Понятие – форма мышления фиксирующая основные, существенные признаки объекта.
Высказывание – это форма мышления, в которой что – либо утверждается или отрицается о реальных предметах, их свойствах и отношениях между ними.
Высказывание может быть истинным или ложным.
Умозаключение – форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (вывод).
Слайд 3Математическая логика является одной из частей формальной логики.
Математическая логика рассматривает только
рассуждения со строго определенными объектами и суждениями, для которых возможно однозначно решить истинны (да, 1) они или ложны (нет, 0).
Основы математической логики положил английский математик Джон Буль, опубликовав в 1854 году книгу «Законы мышления», в которой подробно изложил алгебру логических действий над двоичными числами (Булева алгебра).
Алгебра логики нашла широкое применение в современной компьютерной технике.
Суждения и утверждения в математической логике называются высказываниями и предикатами.
Высказывания это конкретные частные утверждения на которые можно истинны они (Да) или ложны (Нет).
2 + 2 = 4 – истинно (да)
2 * 2 = 5 – ложно (нет)
Предикаты это утверждения истинность которых зависит от значений входящих в них величин
X + Y > 0
Основы математической логики положил английский математик Джон Буль, опубликовав в 1854 году книгу «Законы мышления», в которой подробно изложил алгебру логических действий над двоичными числами (Булева алгебра).
Алгебра логики нашла широкое применение в современной компьютерной технике.
Суждения и утверждения в математической логике называются высказываниями и предикатами.
Высказывания это конкретные частные утверждения на которые можно истинны они (Да) или ложны (Нет).
2 + 2 = 4 – истинно (да)
2 * 2 = 5 – ложно (нет)
Предикаты это утверждения истинность которых зависит от значений входящих в них величин
X + Y > 0
Слайд 4В алгебре логики рассматриваются логические операции
Логическое отрицание «Инверсия»
Логическое сложение «Дизъюнкция»
Логическое умножение
«Конъюнкция»
Логическое следование «Импликация»
Логическое соответствие «Эквивалентность»
Логическое следование «Импликация»
Логическое соответствие «Эквивалентность»
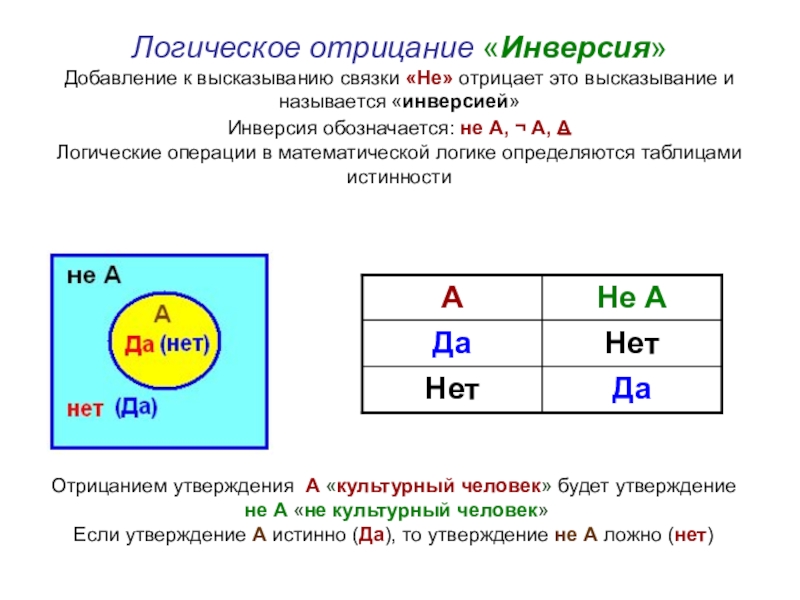
Слайд 5Логическое отрицание «Инверсия» Добавление к высказыванию связки «Не» отрицает это высказывание и
называется «инверсией»
Инверсия обозначается: не А, ¬ А, А
Логические операции в математической логике определяются таблицами истинности
Отрицанием утверждения А «культурный человек» будет утверждение
не А «не культурный человек»
Если утверждение А истинно (Да), то утверждение не А ложно (нет)
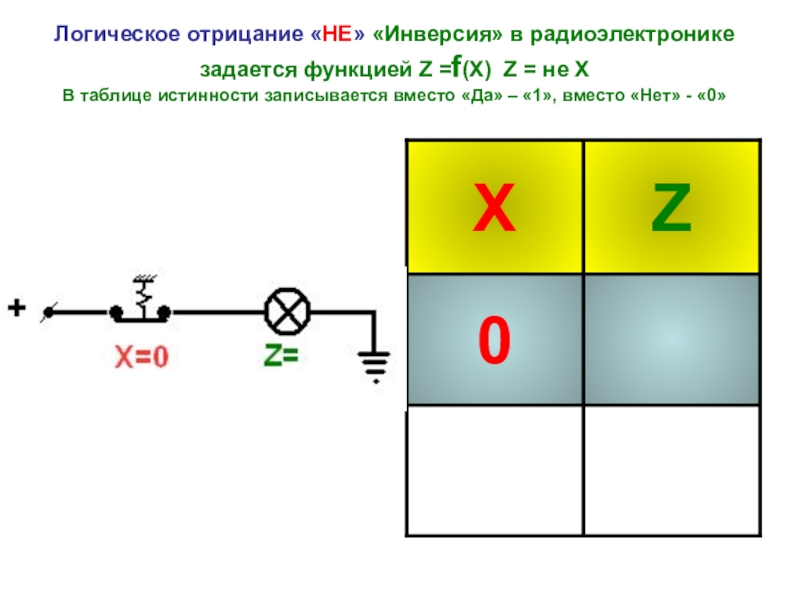
Слайд 6Логическое отрицание «НЕ» «Инверсия» в радиоэлектронике задается функцией Z =f(Х) Z =
не Х
В таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Слайд 7Логическое отрицание «НЕ» «Инверсия» в радиоэлектронике задается функцией Z =f(Х) Z =
не Х
В таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Слайд 8Логическое отрицание «НЕ» «Инверсия» в радиоэлектронике задается функцией Z =f(Х) Z =
не Х
В таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Слайд 9Логическое отрицание «НЕ» «Инверсия» в радиоэлектронике задается функцией Z =f(Х) Z =
не Х
В таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
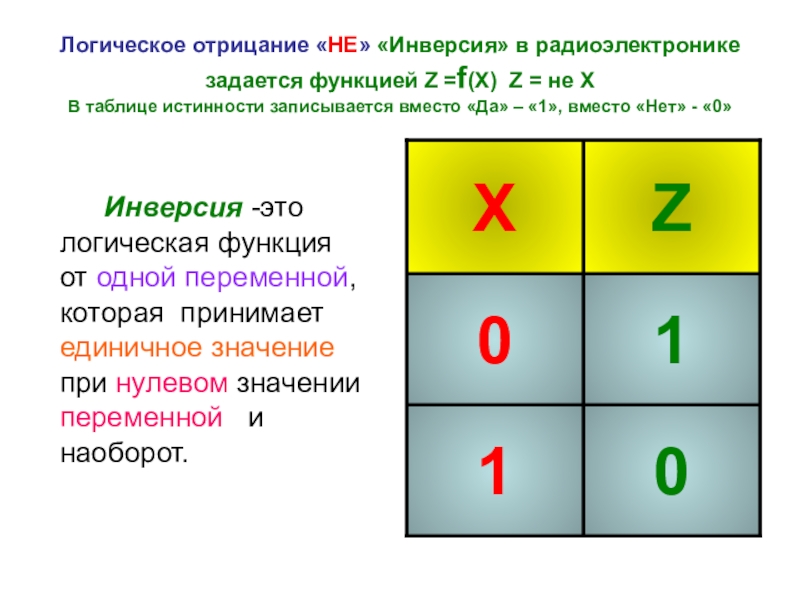
Слайд 10Логическое отрицание «НЕ» «Инверсия» в радиоэлектронике задается функцией Z =f(Х) Z =
не Х
В таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Инверсия -это логическая функция от одной переменной, которая принимает единичное значение при нулевом значении переменной и наоборот.
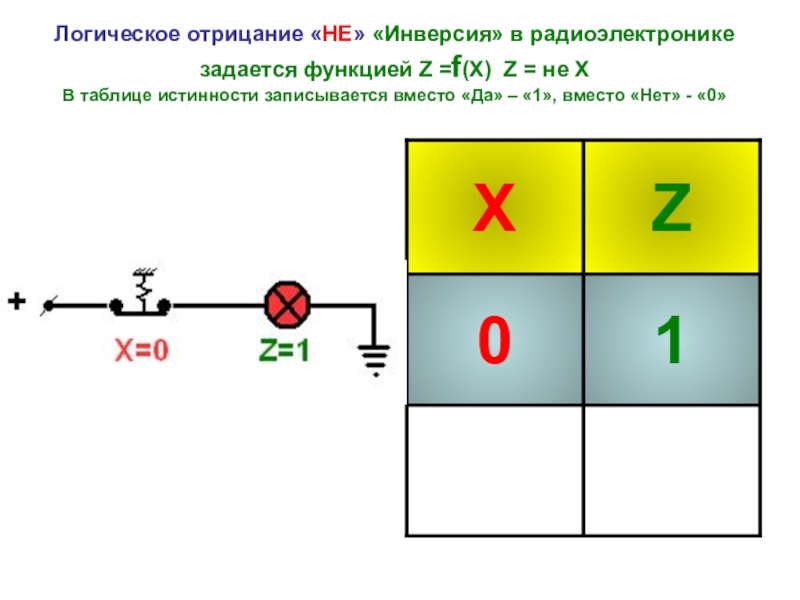
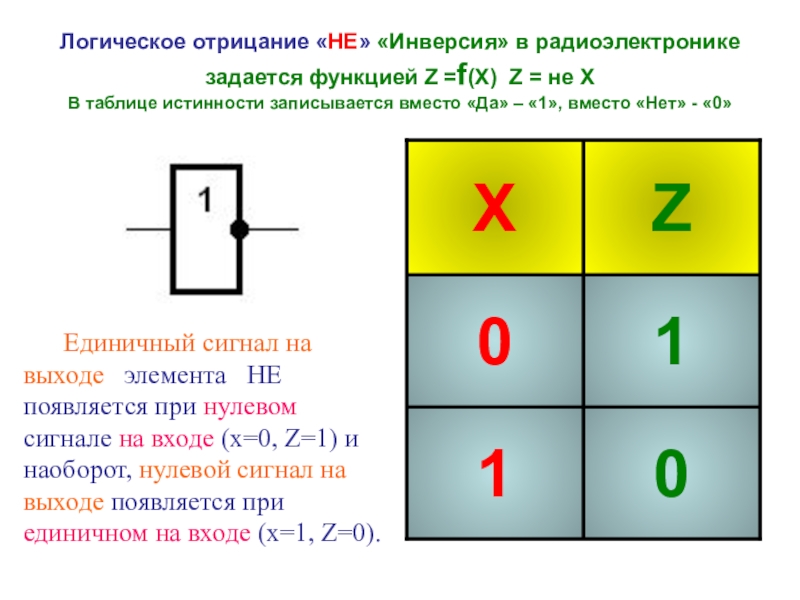
Слайд 11Логическое отрицание «НЕ» «Инверсия» в радиоэлектронике задается функцией Z =f(Х) Z =
не Х
В таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Единичный сигнал на выходе элемента НЕ появляется при нулевом сигнале на входе (х=0, Z=1) и наоборот, нулевой сигнал на выходе появляется при единичном на входе (х=1, Z=0).
Слайд 12Логическое сложение «Дизъюнкция» Соединение двух или нескольких высказываний союзом или называют логическим
сложением «Дизъюнкцией»
Дизъюнкция обозначается: А или В, А v В, А + В
Дизъюнкция в математической логике определяются таблицей истинности
Высказывание: Богатый человек имеет много рублей «А» или много долларов «В» («А или В») истинно:
- если человек имеет много рублей т. е. «А» - «Да», а «В» - «Нет»;
- если человек имеет много долларов т. е. «В» - «Да», а «А» - «Нет» ;
- если человек имеет много рублей и долларов т. е. «А» - «Да», и «В» - «Да»
Слайд 13Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается функцией Z =f(Х,У) Z =
Х v У
в таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Слайд 14Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается функцией Z =f(Х,У) Z =
Х v У
в таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Слайд 15Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается функцией Z =f(Х,У) Z =
Х v У
в таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Слайд 16Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается функцией Z =f(Х,У) Z =
Х v У
в таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Слайд 17Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается функцией Z =f(Х,У) Z =
Х v У
в таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Слайд 18Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается функцией Z =f(Х,У) Z =
Х v У
в таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Слайд 19Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается функцией Z =f(Х,У) Z =
Х v У
в таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Слайд 20Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается функцией Z =f(Х,У) Z =
Х v У
в таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Слайд 21Логическое сложение «или» «Дизъюнкция» в радиоэлектронике задается функцией Z =f(Х,У) Z =
Х v У
в таблице истинности записывается вместо «Да» – «1», вместо «Нет» - «0»
Дизъюнкция -это логическая функция по крайней мере от двух переменных, принимающая единичное значение, когда хотя бы одна из переменных принимает единичное значение.
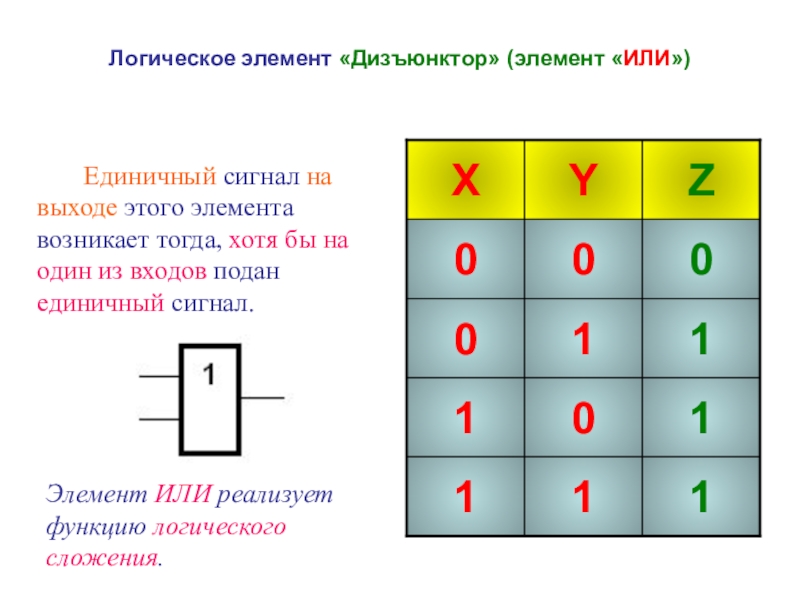
Слайд 22Логическое элемент «Дизъюнктор» (элемент «ИЛИ»)
Единичный сигнал
на выходе этого элемента возникает тогда, хотя бы на один из входов подан единичный сигнал.
Элемент ИЛИ реализует функцию логического сложения.
Слайд 31Логическое умножение «И» «Конъюнкция» Z=XиY, Z=X∧Y, Z=X&Y
Конъюнкция - это логическая функция
по крайней мере от двух переменных, которая принимает единичное значение при единичных значениях всех переменных.
Слайд 32Логическое элемент «Конъюнктор» (элемент «И»)
Единичный сигнал на
выходе этого элемента возникает тогда, и только тогда, когда на все входы поступают единичные сигналы.
Элемент И реализует функцию логического умножения.
