МБОУ СОШ №33
с углубленным изучением английского языка
г. Озерск Челябинская области
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Двоичная арифметика
Содержание
- 1. Двоичная арифметика
- 2. Основной способ представления данных в памяти компьютера
- 3. Слайд 3
- 4. Вещественные числа хранятся и обрабатываются в компьютере
- 5. Число в формате с плавающей запятой может
- 6. знак числазнак порядкапорядокмантиссаЧем больше разрядов отводится под запись мантиссы, тем выше точность представления числа.
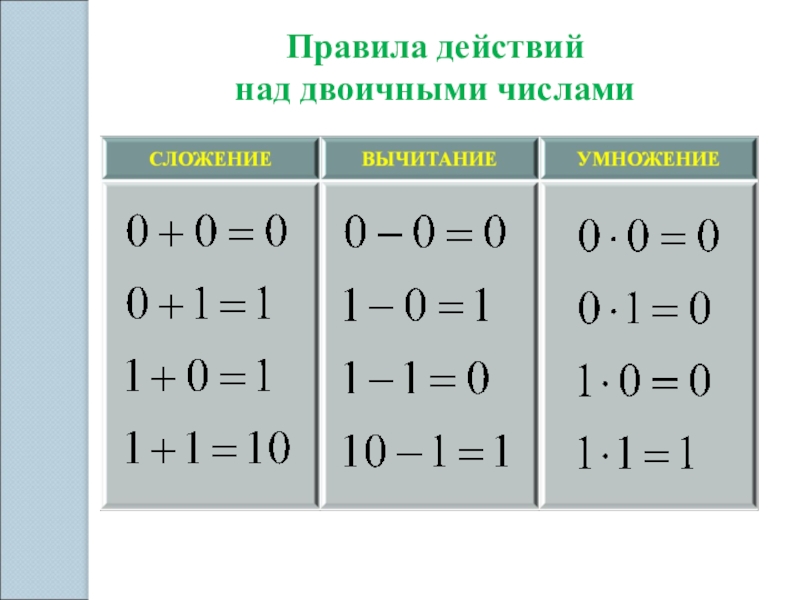
- 7. Правила действий над двоичными числами
- 8. Слайд 8
- 9. Представление чисел в памяти компьютера10011-10011Знаковый разряд располагается
- 10. Для положительных чисел представление числа с прямым,
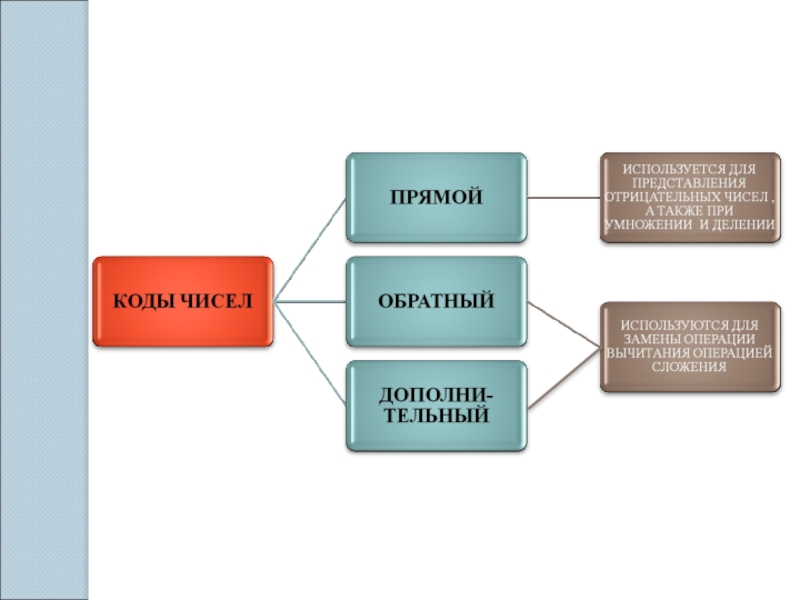
- 11. -10011ПРЯМОЙ КОДОБРАТНЫЙ КОДДОПОЛНИТЕЛЬНЫЙ КОД
- 12. ПРАВИЛА СЛОЖЕНИЯ ЧИСЕЛ В ДВОИЧНОМ КОДЕПри сложении
- 13. Дополнительный код преобразуется в прямой так же,
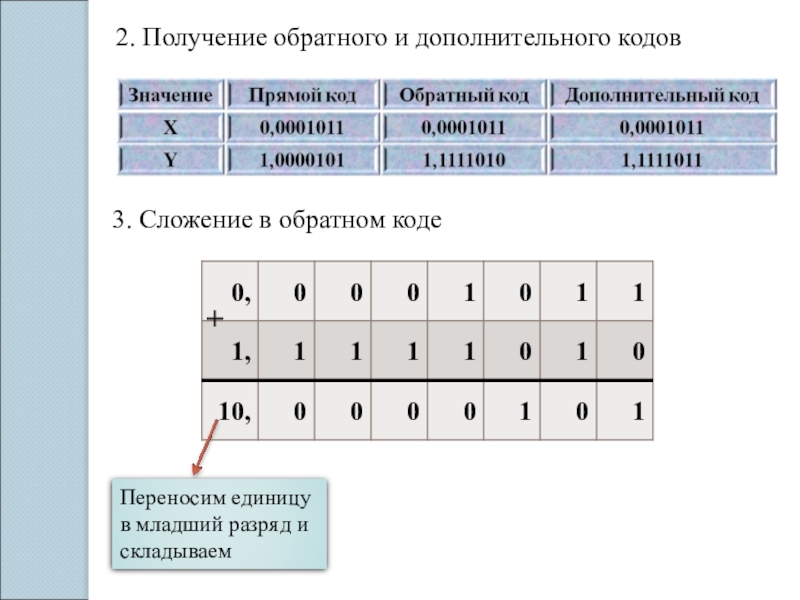
- 14. 2. Получение обратного и дополнительного кодов3. Сложение в обратном коде+Переносим единицу в младший разряд и складываем
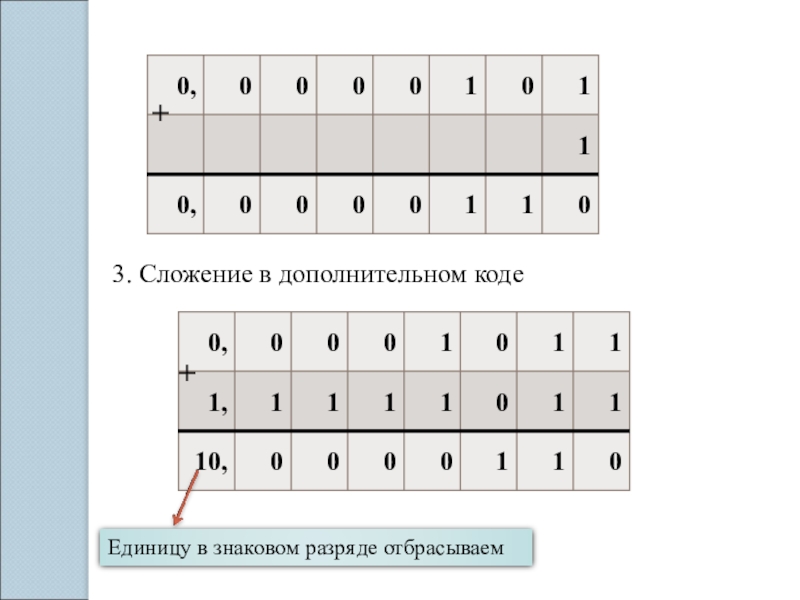
- 15. +3. Сложение в дополнительном коде+Единицу в знаковом разряде отбрасываем
- 16. Записать числа в прямом, обратном и дополнительном
- 17. ДОМАШНЕЕ ЗАДАНИЕ §171.Учить правила арифметических операций.2.
Основной способ представления данных в памяти компьютера – двоичное представление, т.е. основной код – набор из двух символов 0 и 1.
Слайд 1ДВОИЧНАЯ АРИФМЕТИКА
Учитель информатики и ИКТ
М.В. Зинина
Слайд 2Основной способ представления данных в памяти компьютера – двоичное представление, т.е.
основной код – набор из двух символов 0 и 1.
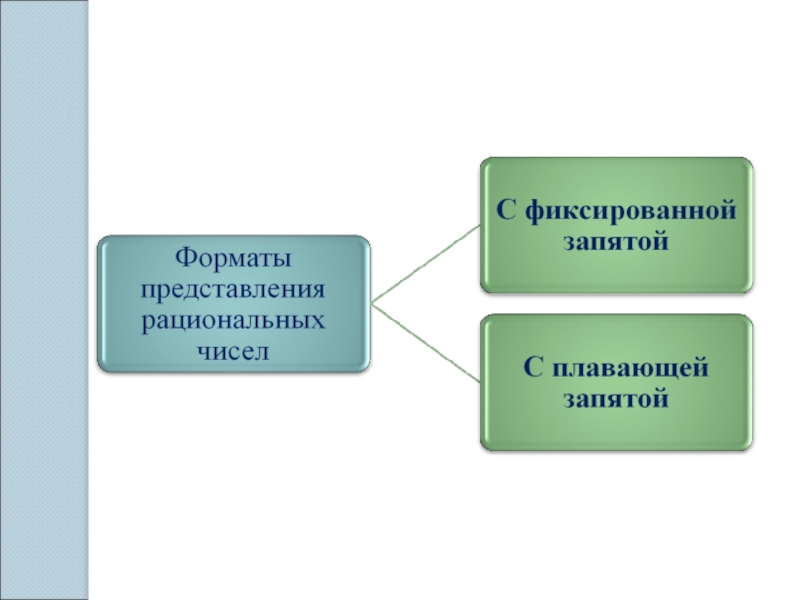
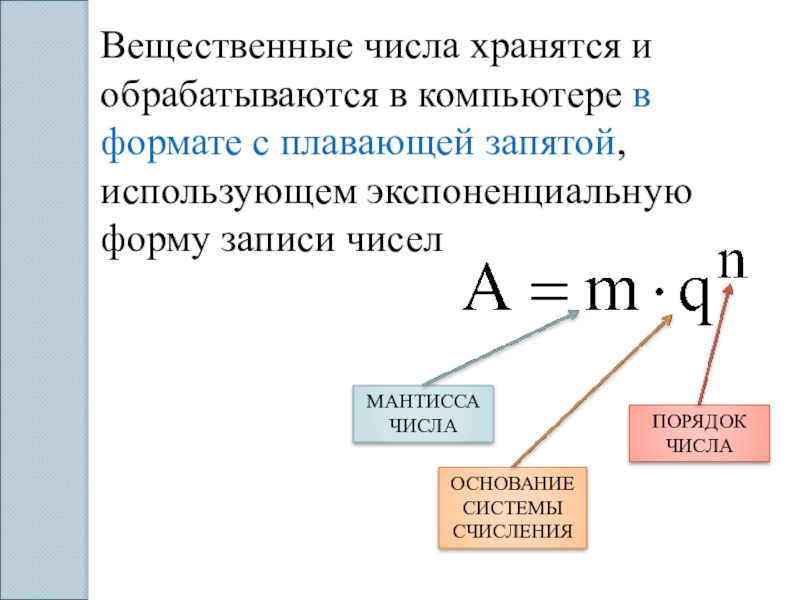
Слайд 4Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей
запятой, использующем экспоненциальную форму записи чисел
МАНТИССА ЧИСЛА
ОСНОВАНИЕ СИСТЕМЫ СЧИСЛЕНИЯ
ПОРЯДОК ЧИСЛА
Слайд 5Число в формате с плавающей запятой может занимать в памяти компьютера
4
байта (обычная точность) или
8 байт (двойная точность).
8 байт (двойная точность).
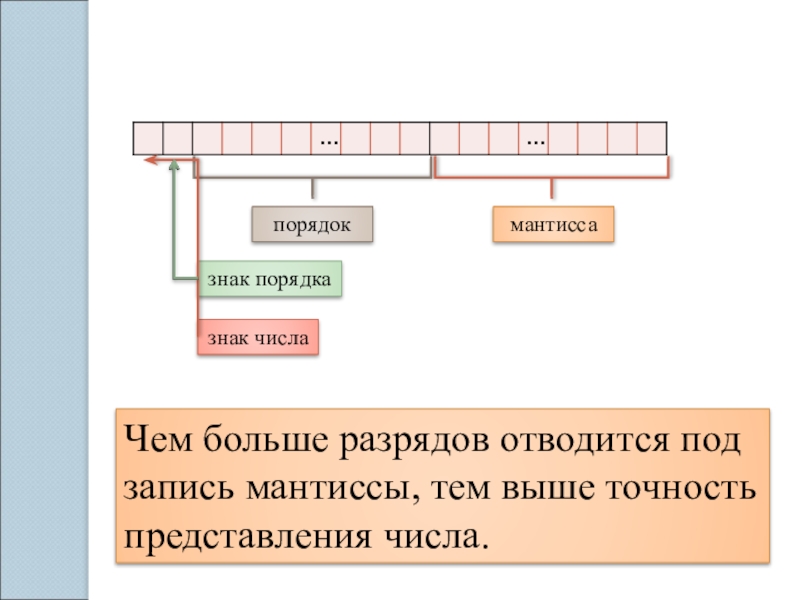
Слайд 6знак числа
знак порядка
порядок
мантисса
Чем больше разрядов отводится под запись мантиссы, тем выше
точность представления числа.
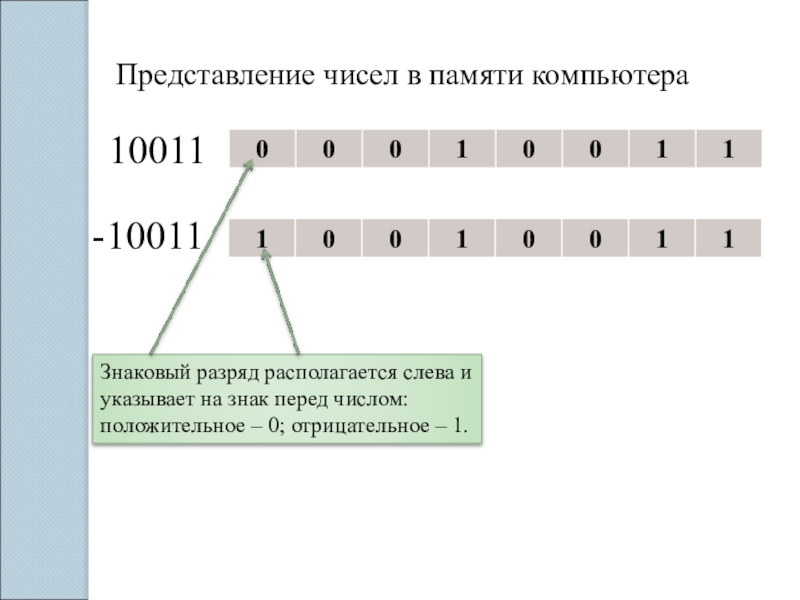
Слайд 9Представление чисел в памяти компьютера
10011
-10011
Знаковый разряд располагается слева и указывает на
знак перед числом: положительное – 0; отрицательное – 1.
Слайд 10Для положительных чисел представление числа с прямым, обратным и дополнительным кодом
совпадают.
Для отрицательных чисел:
1) при обратном коде все числа (кроме знакового разряда) инвертируются;
2) при дополнительном коде к значению с обратным кодом добавляется единица.
Слайд 12ПРАВИЛА СЛОЖЕНИЯ ЧИСЕЛ В ДВОИЧНОМ КОДЕ
При сложении чисел в дополнительном коде
возникающая единица переноса в знаковом разряде отбрасывается.
При сложении чисел в обратном коде возникающая единица переноса в знаковом разряде прибавляется к младшему разряду суммы кодов.
Если результат арифметических действий является кодом отрицательного числа, то его необходимо преобразовать в прямой код.
При этом обратный код преобразуется в прямой инвертированием цифр во всех разрядах кроме знакового.
Слайд 13Дополнительный код преобразуется в прямой так же, как и обратный с
последующим прибавлением единицы к младшему разряду.
Пример. Сложить числа Х = 1011 и Y = -101 в обратном и дополнительном кодах.
1. Произведем сложение по правилам двоичной арифметики
Слайд 142. Получение обратного и дополнительного кодов
3. Сложение в обратном коде
+
Переносим единицу
в младший разряд и складываем
Слайд 16Записать числа в прямом, обратном и дополнительном кодах: 1010; -1101; -10101;
-10011
Преобразуйте прямой код 1,110001 в двоичное число, переведите его в десятичную систему счисления
Слайд 17ДОМАШНЕЕ ЗАДАНИЕ §17
1.Учить правила арифметических операций.
2. Записать числа 1110100 и
-101101 в прямом, обратном и дополнительном кодах; сложить их в обратном и дополнительном кодах.
3. Перевести прямой код в двоичное число, записать его в десятичной системе счисления 0,100111; 1,1001100
3. Перевести прямой код в двоичное число, записать его в десятичной системе счисления 0,100111; 1,1001100
