Презентация, доклад по химии Математическая обработка результатов физико-химического эксперимента

Математическая статистика – это наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов.

Диссоциация воды. Ионное произведение воды. pH.

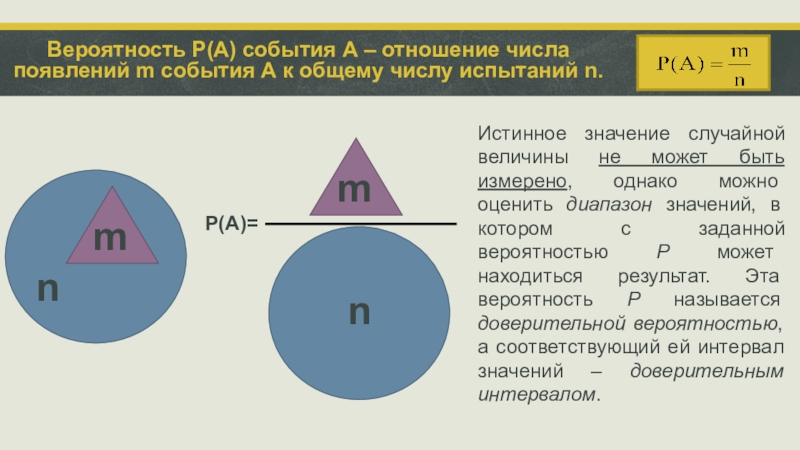
Вероятность Р(А) события А – отношение числа появлений m события А к общему числу испытаний n.

Истинное значение случайной величины не может быть измерено, однако можно оценить диапазон значений, в котором с заданной вероятностью P может находиться результат. Эта вероятность P называется доверительной вероятностью, а соответствующий ей интервал значений – доверительным интервалом.

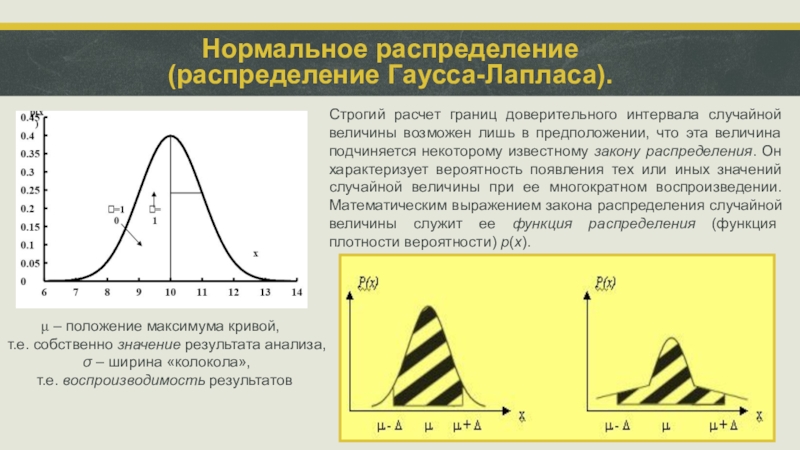
Нормальное распределение
(распределение Гаусса-Лапласа).

Строгий расчет границ доверительного интервала случайной величины возможен лишь в предположении, что эта величина подчиняется некоторому известному закону распределения. Он характеризует вероятность появления тех или иных значений случайной величины при ее многократном воспроизведении. Математическим выражением закона распределения случайной величины служит ее функция распределения (функция плотности вероятности) p(x).

– положение максимума кривой,
т.е. собственно значение результата анализа,
 – ширина «колокола»,
т.е. воспроизводимость результатов

Дефект массы – уменьшение массы атома по сравнению с суммарной массой всех отдельно взятых составляющих его элементарных частиц, обусловленное энергией их связи в атоме.

Относительная атомная масса элемента равна среднему значению из массовых чисел всех его природных изотопов с учетом их распространенности.

где W1, W2, ..., Wi – доля 1-го, 2-го, ..., i-го изотопа;
А1, А2, ..., Аi – массовые числа атома 1-го, 2-го, ..., i-го изотопа;
n – общее число изотопов данного элемента.

E – полная энергия системы,
c = 3.1010 см/сек – скорость света в вакууме,
m – масса атома

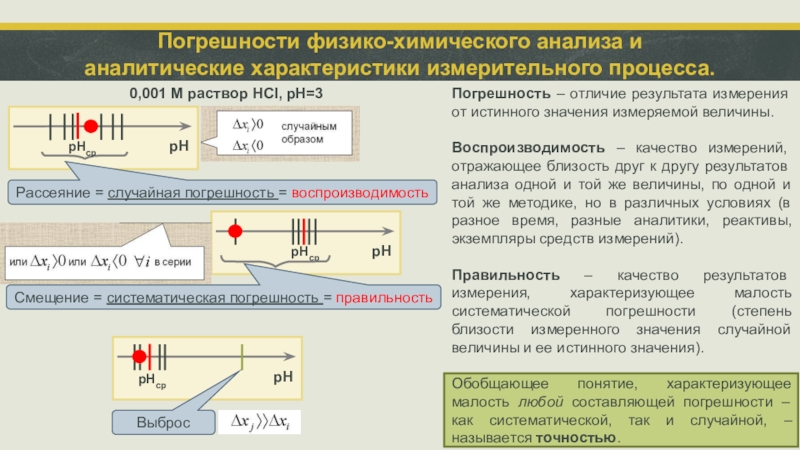
Погрешности физико-химического анализа и
аналитические характеристики измерительного процесса.

Погрешность – отличие результата измерения от истинного значения измеряемой величины.

Воспроизводимость – качество измерений, отражающее близость друг к другу результатов анализа одной и той же величины, по одной и той же методике, но в различных условиях (в разное время, разные аналитики, реактивы, экземпляры средств измерений).

Правильность – качество результатов измерения, характеризующее малость систематической погрешности (степень близости измеренного значения случайной величины и ее истинного значения).

Обобщающее понятие, характеризующее малость любой составляющей погрешности – как систематической, так и случайной, – называется точностью.

0,001 M раствор HCl, pH=3

pHср

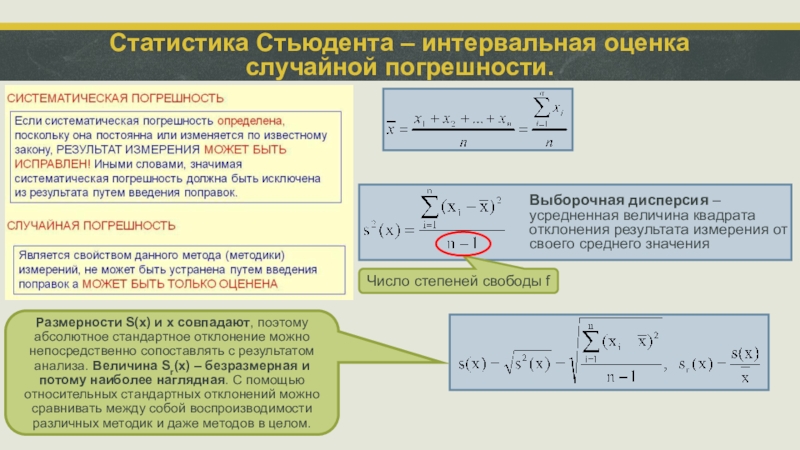
Статистика Стьюдента – интервальная оценка
случайной погрешности.

Размерности S(x) и x совпадают, поэтому абсолютное стандартное отклонение можно непосредственно сопоставлять с результатом анализа. Величина Sr(x) – безразмерная и потому наиболее наглядная. С помощью относительных стандартных отклонений можно сравнивать между собой воспроизводимости различных методик и даже методов в целом.

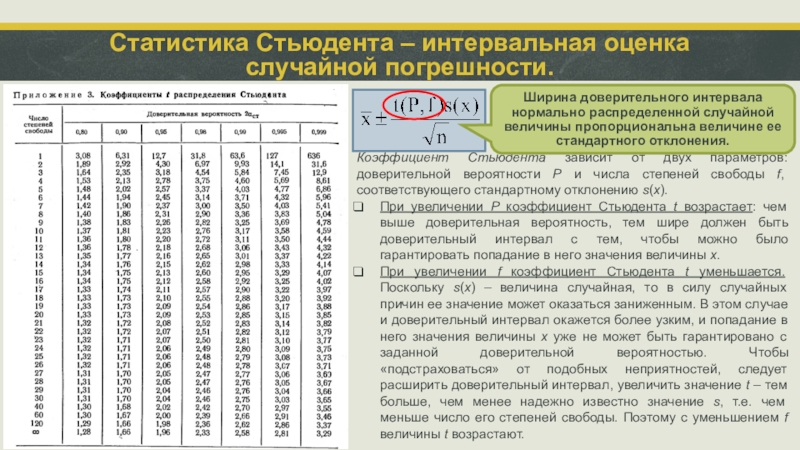
Коэффициент Стьюдента зависит от двух параметров: доверительной вероятности P и числа степеней свободы f, соответствующего стандартному отклонению s(x).
При увеличении P коэффициент Стьюдента t возрастает: чем выше доверительная вероятность, тем шире должен быть доверительный интервал с тем, чтобы можно было гарантировать попадание в него значения величины x.
При увеличении f коэффициент Стьюдента t уменьшается. Поскольку s(x) – величина случайная, то в силу случайных причин ее значение может оказаться заниженным. В этом случае и доверительный интервал окажется более узким, и попадание в него значения величины x уже не может быть гарантировано с заданной доверительной вероятностью. Чтобы «подстраховаться» от подобных неприятностей, следует расширить доверительный интервал, увеличить значение t – тем больше, чем менее надежно известно значение s, т.е. чем меньше число его степеней свободы. Поэтому с уменьшением f величины t возрастают.

Статистика Стьюдента – интервальная оценка
случайной погрешности.

Ширина доверительного интервала нормально распределенной случайной величины пропорциональна величине ее стандартного отклонения.

Критерии проверки выборки на наличие грубых промахов.

Q-критерии. Тестовая статистика Q-критерия верна для числа измерений m=3..7. При m=8…10 в знаменателе должна стоять разница между подозрительным значением и ближайшем к максимальному (или минимальному). Значение Q сравнивают с табличным значением, и если табличное значение критерия меньше тестовой статистики, то подозрительный результат является промахом и исключается из дальнейшего рассмотрения. При этом обычно доверительную вероятность берут равной 0.90, а не 0.95. В данном случае это является некоторым "ужесточением" требований: лучше выбросить значение, не являющееся промахом, чем оставить промах в выборке. Как правило, на промах проверяют минимальное и максимальное значение выборки. Q-критерий работает для выборок, содержащих 3-10 значений, при больших объемах выборки он становится нечувствителен к промахам.
Критерий Стьюдента. Минимальное и максимальное значения xкр являются грубыми промахами, если параметр τ, превышает табличный τкр для принятой доверительной вероятности и числе степеней свободы f=m-1. Критерий Стьюдента является более универсальным, поскольку позволяет учесть разброс данных внутри выборки относительно друг друга.

,