- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Вычисление площадей простых фигур
Содержание
- 1. Вычисление площадей простых фигур
- 2. Геометрические паркеты Паркет (или мозаика) - бесконечное
- 3. Паркеты из одинаковых правильных многоугольниковСумма всех углов
- 4. Паркеты из разных правильных
- 5. Можно показать, что существуют следующие способы уложить
- 6. Паркеты из неправильных
- 7. До сих пор не найдены все типы
- 8. Паркеты из произвольных фигур Некоторые определения паркета
- 9. Способ первый. Берем некоторую сетку (уже известный
- 10. Способ второй. Объединяем отдельные элементы уже существующих
- 11. Паркет, каждый элемент которого получен в результате объединения пяти правильных треугольников:
- 12. Способ третий. Берем существующую сетку и дополняем
- 13. Способ четвертый. Выбираем некоторую кривую или ломаную
- 14. А вот паркеты, полученные с помощью параллельного
- 15. А так же паркеты из элементов окружности
- 16. Паркет — натуральное деревянное напольное покрытие. Современный
- 17. Укладка штучного паркета Для настилки
- 18. Пол прямоугольной формы 4м на
- 19. Площадь данного прямоугольника 20*(11*35 +15)=8000см.кв. 200000:8000=25рядов 2*25=50 треугольников
Слайд 2Геометрические паркеты
Паркет (или мозаика) - бесконечное семейство многоугольников, покрывающее плоскость без
Итак, какими же многоугольниками можно замостить плоскость?
Слайд 3Паркеты из одинаковых правильных многоугольников
Сумма всех углов n-угольника равна 180°(n-2). Все
Разность n-2 может принимать лишь значения 1, 2 или 4; поэтому n может быть равно только 3, 4 или 6. Значит, можно получить паркеты, составленные из правильных треугольников, квадратов или правильных шестиугольников.
Слайд 4 Паркеты из разных правильных
Сначала выясним, какое количество различных правильных многоугольников (с одинаковыми длинами сторон) может находиться вокруг каждой точки. Величина угла правильного многоугольника должна находиться в интервале от 60° до 180° (не включая); следовательно, число многоугольников, находящихся в окрестности точки, должно быть больше 2 (360°/180°) и не может превышать 6 (360°/60°).
Слайд 5Можно показать, что существуют следующие способы уложить паркет комбинациями правильных многоугольников:
Слайд 6 Паркеты из неправильных
Легко покрыть плоскость параллелограммами:
Вообще можно замостить плоскость копиями произвольного четырехугольника, необязательно выпуклого:
Можно составить паркет из копий произвольного треугольника:
Слайд 7До сих пор не найдены все типы выпуклых пятиугольников, из которых
Еще плоскость можно покрыть копиями центрально-симметричного шестиугольника, или копиями пятиугольника с двумя параллельными сторонами.
Слайд 8Паркеты из произвольных фигур
Некоторые определения паркета не ограничиваются многоугольниками; в этом
В таком случае даже для паркетов из многоугольников может не соблюдаться требование "два многоугольника должны иметь общую вершину, общую сторону или совсем не иметь общих точек"; кроме того, появляется множество разнообразных паркетов, состоящих не из многоугольников, а из криволинейных фигур. Рассмотрим способы построения нового паркета, исходя из этого "расширенного" определения. Итак, как нарисовать паркет? (некоторые из возможных способов)
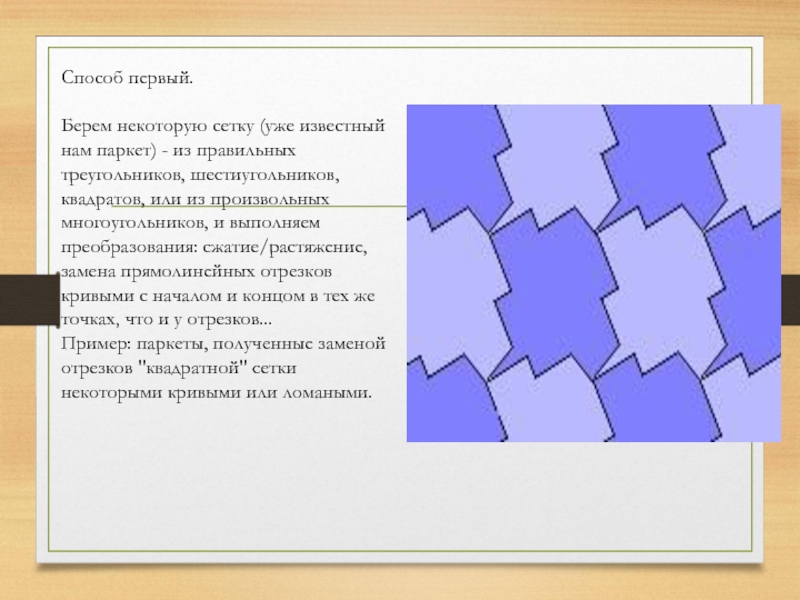
Слайд 9Способ первый.
Берем некоторую сетку (уже известный нам паркет) - из
Пример: паркеты, полученные заменой отрезков "квадратной" сетки некоторыми кривыми или ломаными.
Слайд 10Способ второй.
Объединяем отдельные элементы уже существующих паркетов. Примеры: паркеты, полученные
Слайд 11Паркет, каждый элемент которого получен в результате объединения пяти правильных треугольников:
Слайд 12Способ третий.
Берем существующую сетку и дополняем ее новыми линиями. Получаем
Пример (разбиения сетки из греческих крестов):
Слайд 13Способ четвертый.
Выбираем некоторую кривую или ломаную и начинаем ее переносить
Для получения данного паркета была взята дуга спирали, три раза повернута на 90°, а затем к получившейся фигуре был применен параллельный перенос
Слайд 14А вот паркеты, полученные с помощью параллельного переноса звездчатых многоугольников:
Совмещая вершины
Слайд 16Паркет — натуральное деревянное напольное покрытие. Современный паркет многолик — от
Слайд 17 Укладка штучного паркета
Для настилки штучного паркета используют несколько методов.
Палуба» - самый простой рисунок укладки. При котором планки располагают параллельно друг другу в продольном направлении.
«Вьетнамка», которая представляет собой переплетение продольных и поперечных плашек, также устойчива к деформации.
«Елочка» была и есть исторически самой распространенной укладкой в России. Деформация паркета, уложенного «елочкой», минимальна.
.
Слайд 18
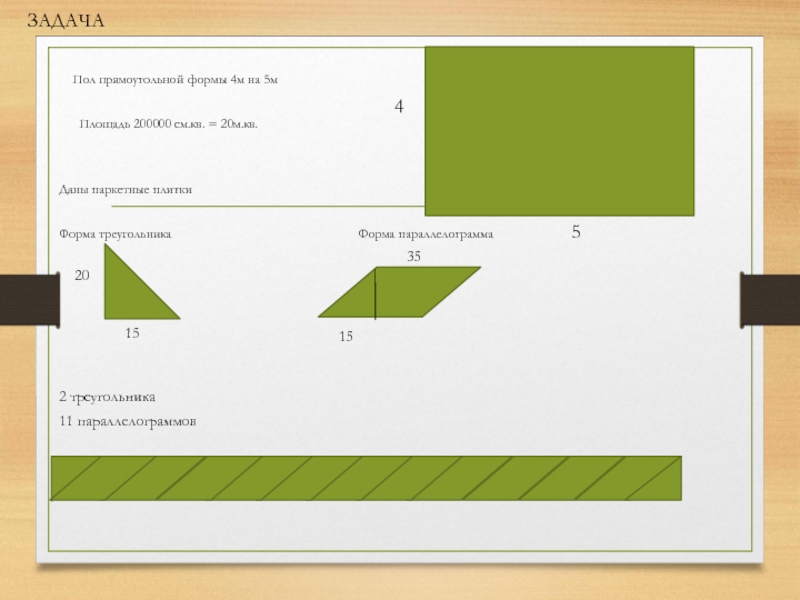
Пол прямоугольной формы 4м на 5м
Площадь
Даны паркетные плитки
Форма треугольника Форма параллелограмма
2 треугольника
11 параллелограммов
4
5
15
15
35
20
ЗАДАЧА
Слайд 19Площадь данного прямоугольника 20*(11*35 +15)=8000см.кв.
200000:8000=25рядов
2*25=50 треугольников
11*25=275 параллелограммов
50*30=1500рублей 18000рублей стоимость материалов
275*60=16500рублей
Т.к. площадь пола 200000 см.кв. = 20м.кв. то стоимость услуги настила паркета обойдется в 20*500=10000рублей
18000+10000=28000 рублей
Ответ: 28 тысяч рублей требуется на материалы и работу при настиле паркета.