- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Векторы.Повторение
Содержание
- 1. Векторы.Повторение
- 2. Найти координаты точек А, В, С и
- 3. * * -120* * 12 -1,5Коллинеарны ли векторы 3 68 6 12 16= 2или
- 4. Векторы называются компланарными, если
- 5. BA(3;5;7),(5;4;-1),PC(2;-1;0),(4;-4;2),D(-3;-4;0),RT(-4;0;-4),(0;5;-1),N(3;2;-3),B(5;4;-1)A(3;5;7)C(4;-4;2)P(2;-1;0)T(0; 5;-1)R(-4;0;-4)O(0;0;0),O(0;0;0),ABON
- 6. Найдите координаты векторовR(2; 7;1)M(-2;7;3)R(2;7;1); M(-2;7;3); RMP(-5;1;4); D(-5;7;-2);
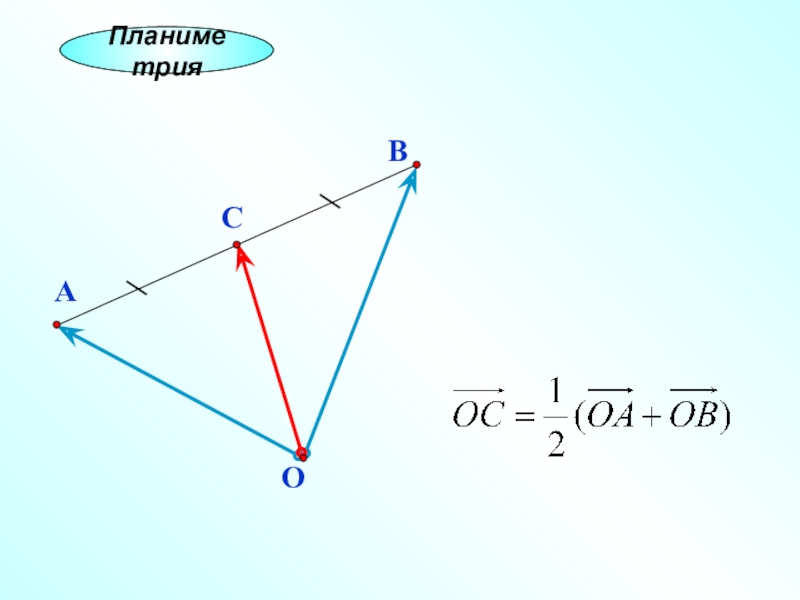
- 7. BПланиметрия A
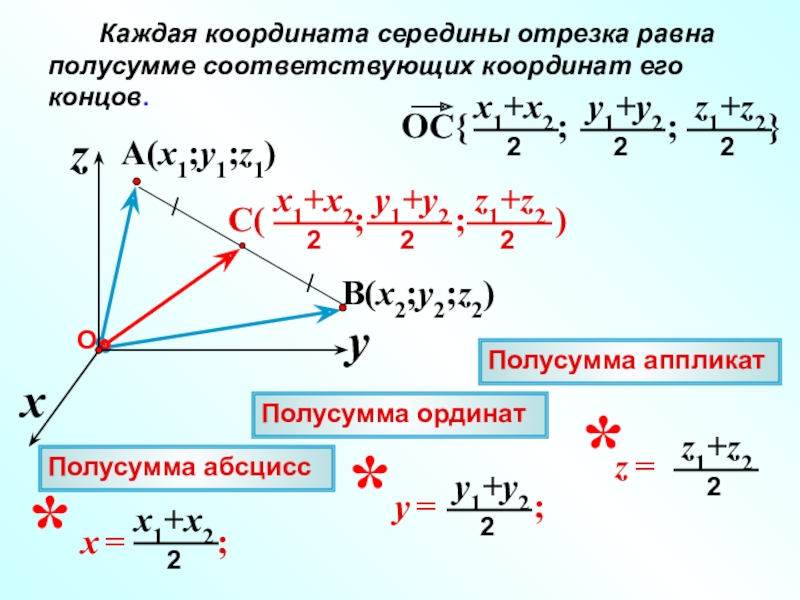
- 8. A(x1;y1;z1)xzyB(x2;y2;z2) Каждая координата середины
- 9. -1( ; ;
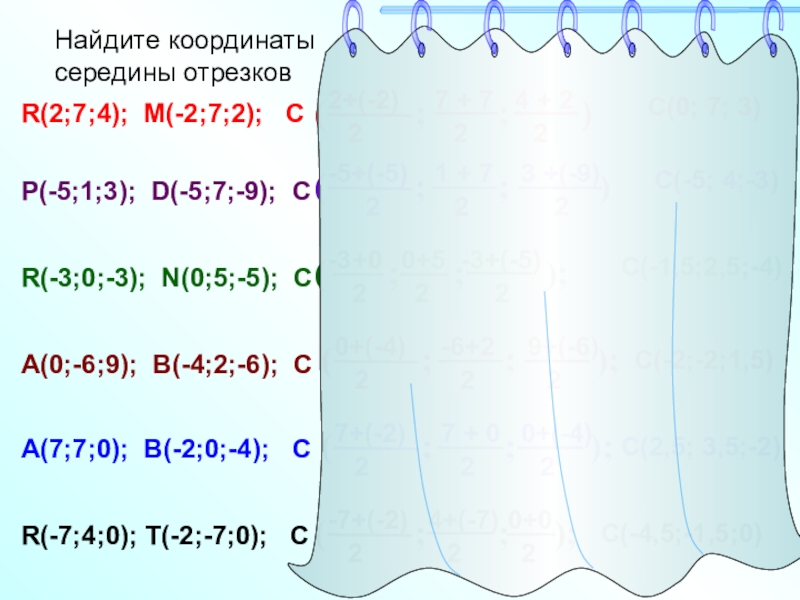
- 10. Найдите координаты середины отрезковR(2;7;4); M(-2;7;2); CP(-5;1;3);
- 11. Дано: Найти: A(5;
- 12. Слайд 12
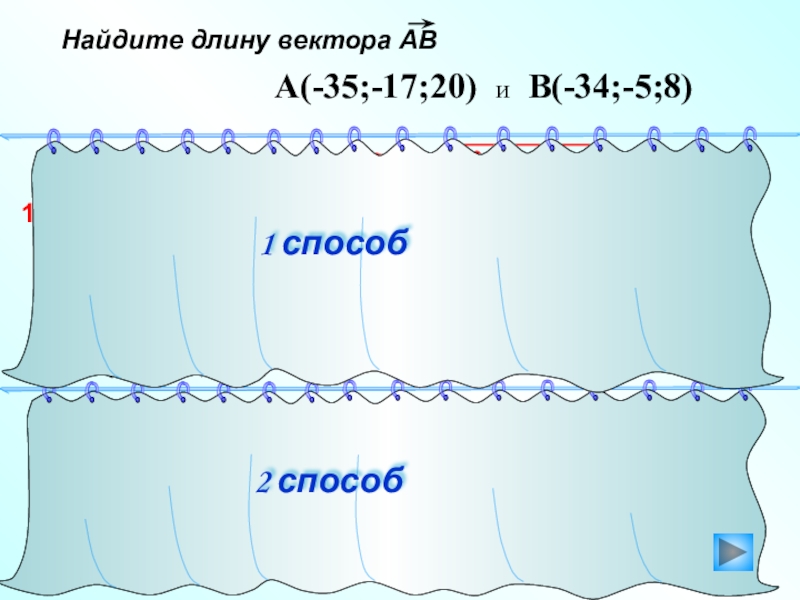
- 13. Найдите длину вектора АВ 1 способ2 способ12+122+(-12)2 =1)2)= 17A(-35;-17;20) и B(-34;-5;8)A(-35;-17;20)B(-34; -5; 8)
- 14. ( )( )
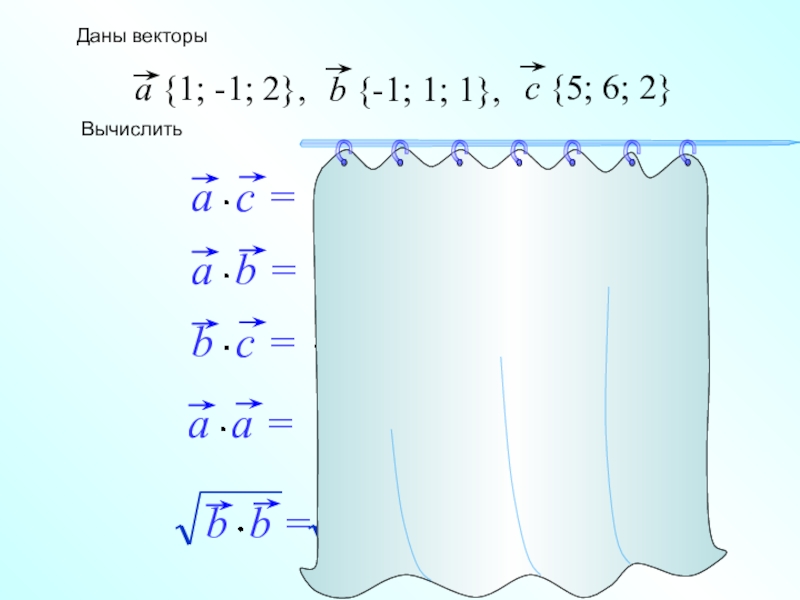
- 15. Даны векторы Вычислить
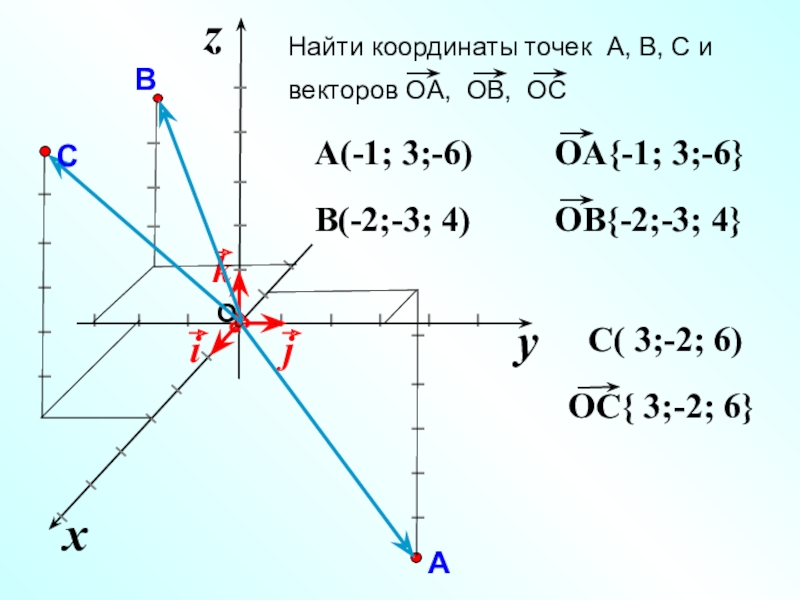
Слайд 2Найти координаты точек А, В, С и
векторов ОА, ОВ, ОС
A(-1; 3;-6)
B(-2;-3; 4)
y
x
z
I I I I I I I I
I I I I I
I I I I I I I I
O
C( 3;-2; 6)
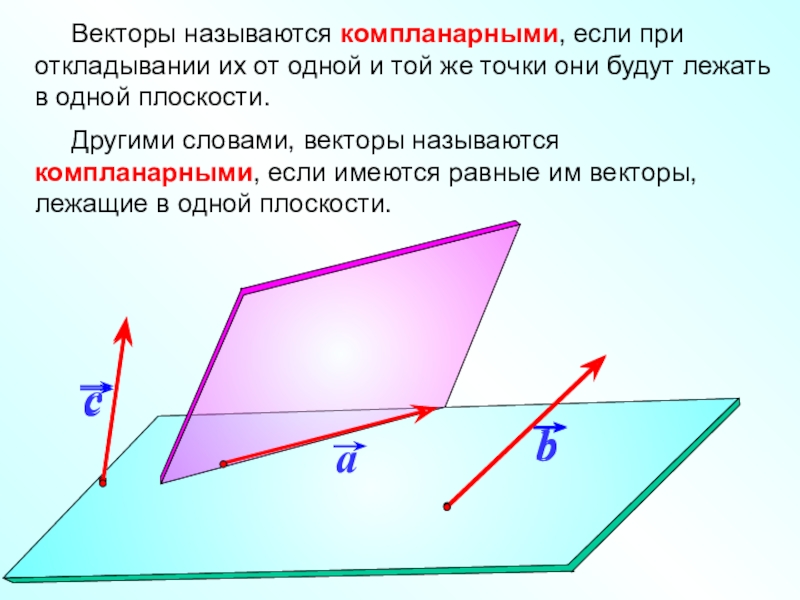
Слайд 4 Векторы называются компланарными, если при откладывании их от
Другими словами, векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Слайд 5B
A
(3;5;7),
(5;4;-1),
P
C
(2;-1;0),
(4;-4;2),
D
(-3;-4;0),
R
T
(-4;0;-4),
(0;5;-1),
N
(3;2;-3),
B(5;4;-1)
A(3;5;7)
C(4;-4;2)
P(2;-1;0)
T(0; 5;-1)
R(-4;0;-4)
O
(0;0;0),
O
(0;0;0),
AB
ON
Слайд 6
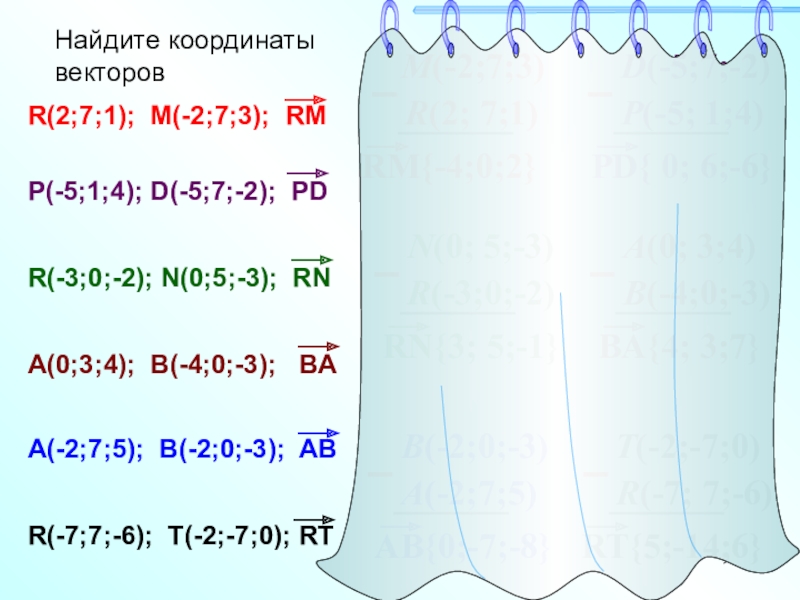
Найдите координаты
векторов
R(2; 7;1)
M(-2;7;3)
R(2;7;1); M(-2;7;3); RM
P(-5;1;4); D(-5;7;-2); PD
P(-5; 1;4)
D(-5;7;-2)
R(-3;0;-2); N(0;5;-3); RN
A(0;3;4);
R(-7;7;-6); T(-2;-7;0); RT
A(-2;7;5); B(-2;0;-3); AB
R(-3;0;-2)
N(0; 5;-3)
B(-4;0;-3)
A(0; 3;4)
A(-2;7;5)
B(-2;0;-3)
R(-7; 7;-6)
T(-2;-7;0)
Слайд 8A(x1;y1;z1)
x
z
y
B(x2;y2;z2)
Каждая координата середины отрезка равна полусумме соответствующих
Полусумма абсцисс
Полусумма ординат
Полусумма аппликат
*
*
*
Слайд 9-1
( ; ; )
A(0; 3;-4),
B(-2;2;0), середина –
M
Полусумма абсцисс
Полусумма ординат
Полусумма аппликат
2,5
-2
= -1
= 2,5
= -2
Найдите координаты середины отрезка
Слайд 10
Найдите координаты
середины отрезков
R(2;7;4); M(-2;7;2); C
P(-5;1;3); D(-5;7;-9); C
R(-3;0;-3);
A(0;-6;9); B(-4;2;-6); C
R(-7;4;0); T(-2;-7;0); C
A(7;7;0); B(-2;0;-4); C
Слайд 11Дано:
Найти:
A(5; 4; -6);
C(-3;
B(a; b;c)
Обратная задача.
x
x1
y
x2
y1
y2
– 6 = 5 + a
a = – 11
4 = 4 + b
b = 0
B(-11; 0;26)
z2
z1
z
20 = -6 + c
c = 26
Слайд 13Найдите длину вектора АВ
1 способ
2 способ
12+122+(-12)2 =
1)
2)
= 17
A(-35;-17;20) и B(-34;-5;8)
A(-35;-17;20)
B(-34;
Слайд 14( )
( )
и
выражается формулой
a {x1; y1;z1}
b {x2; y2;z2}
= x1x2 + y1y2+z1z2
5
+
-
1
4
= 15
-7
-3
+