Презентация, доклад на тему Урок - презентация по теме: Разность квадратов

формулы , но и уметь их правильно применять!

Актуализация знаний

1.Найдите квадраты одночленов: (1,1 х)²; (4р²)²;
(-9ху³)²; (3р³ⁿˉ²)².
2.Являются ли тождеством следующие равенства:
4х² = (4х)²; (5у)² = 25у².
Важны ли скобки в подобных записях?
3. Выполните умножение:
(8х - 5у)(8х +5у);
(х² - 2у³)(х² + 2у³)
(а – в)(а + в).
Какой можно сделать вывод?
4. Пробное задание:
199 ∙201

Работа в группах

Задание I группе
Доказать тождество:
(а-в)(а+в) =а²-в²
Сформулировать правило
Составить алгоритм работы по формуле.

Задание II группе
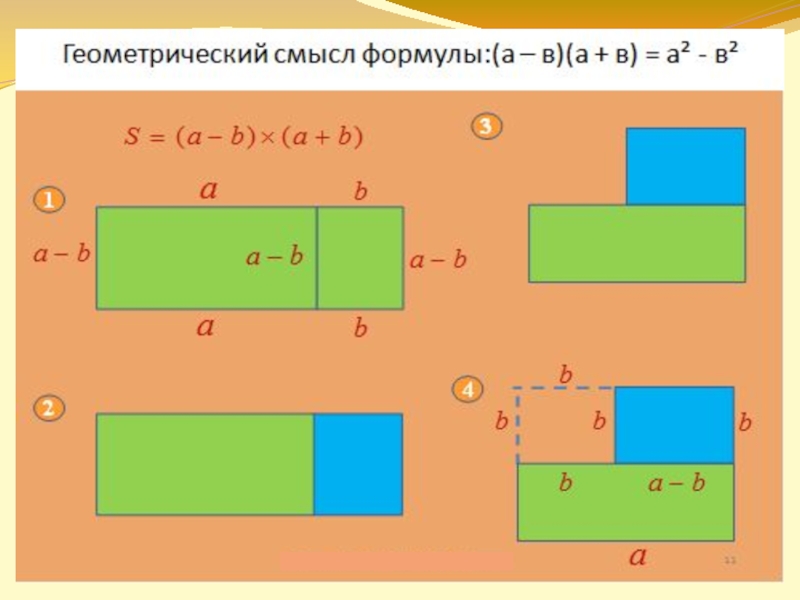
Используя рисунок, разъяснить геометрический смысл формулы (а-в)(а+в) =а²-в²
при а>0; в>0 и а>в.

Формулы сокращенного умножения.

Выполнив умножение разности двух выражений на сумму этих же выражений:
(а – в)(а + в) = а²- ав +ав - в² = а²- в²
Получим: (а – в)(а + в) = а²- в² (1)
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Тождество (1) является одной из формул сокращенного умножения.
Оно позволяет сокращенно выполнять умножение разности любых двух выражений и их сумму.

умножения были известны около 4000 лет назад. Их знали, кроме вавилонян, и другие народы древности, конечно, не в нашем символическом виде, а словесно или в геометрической форме.

Первичное закрепление

Работа с учебником
Надо не только знать формулы, но уметь их правильно применять!
Стр. 148, п.24 прочитать правило
№728(ж)
№729(в)
№733(г)
№739(г)
с/р

Самостоятельная работа.

Выполните умножение:
1. (4 +у²)(у² - 4);
2. (0,7х +у⁴)( 0,7х – у⁴);
3. 69∙71;
4. Дополнительно.
Найдите значение выражения выполнив соответствующие преобразования:
(2-1)(2+1)(2²+1)(2⁴+1)(2⁸+1) - 2¹⁶.

образцу(работа в парах)

(4 +у²)(у²- 4) = (у²)² - 4² = у⁴ - 16;
(0,7х+у⁴)(0,7х–у⁴)=(0,7х)²-(у⁴)²=(0,7)²х²- у⁸=0,49х²-у⁸;
69∙70 = (70 – 1)(70 +1) =70² -1² =4900 – 1= 4899;
(2-1)(2+1()(2²+1)(2⁴+1)(2⁸+1) -2¹⁶=
=(2²-1)(2²+1)(2⁴+1)(2⁸+1)–2¹⁶=(2⁴-1)(2⁴+1)∙ ∙(2⁸+1)–2¹⁶=(2⁸-1)(2⁸+1)–2¹⁶=(2¹⁶-1)-2¹⁶= -1

Включение в систему знаний

Любопытный факт, связанный с нашей формулой.
Возьмем несколько «троек» любых, но последовательных целых чисел.
Например: 3;4;5 или 20;21;22 и т. д.
Сравним в каждой из них квадрат среднего числа и произведение последующего и предыдущего целых чисел.
Вывод: квадрат среднего числа на 1 больше предыдущего и последующего целых чисел.
Это случайное совпадение или закономерность?
Попробуйте рассуждать в общем виде.

:
n-1; n; n+1.
Теперь составим выражения для квадрата среднего числа и произведения крайних чисел.
Получаем ожидаемый вывод:
n²; (n – 1)∙(n +1) = n²- 1
Квадрат среднего числа на 1 больше предыдущего и последующего целых чисел.

(а,б)
№733 (б)
№739(а,б)
3. Пифагор утверждал, что «Всякое нечетное число кроме 1, есть разность двух квадратов».
Прав ли был Пифагор?
И как это можно проверить?