- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Ученический проект Страна треугольников
Содержание
- 1. Ученический проект Страна треугольников
- 2. Цель Систематизировать и расширить знания о треугольниках
- 3. Задачи:изучить исторические сведения о треугольниках; исследовать геометрические
- 4. Исторические сведения Треугольник - самая простая замкнутая
- 5. ТРЕУГОЛЬНИКВСАВ – простейший многоугольник, имеющий 3 вершины (угла)
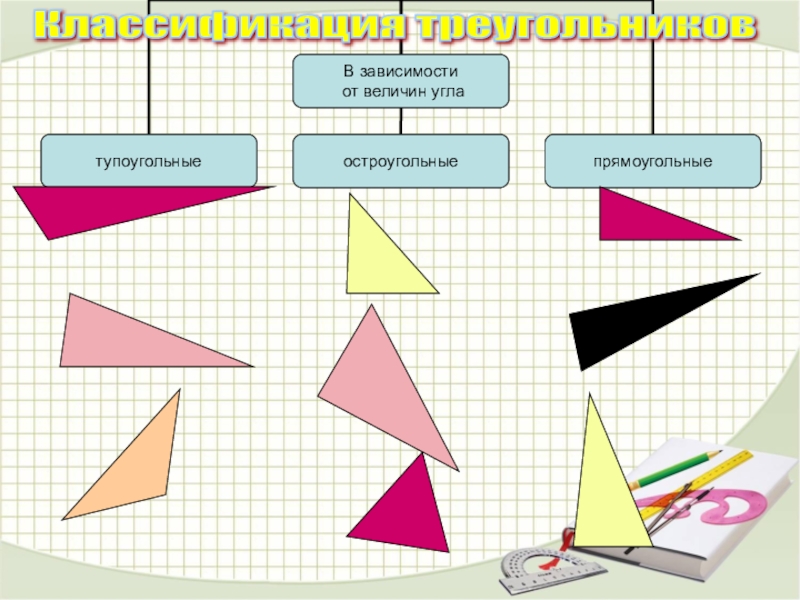
- 6. Классификация треугольников
- 7. Если все три угла острые ( рис.20 ), то это остроугольный треугольник. Если один из углов
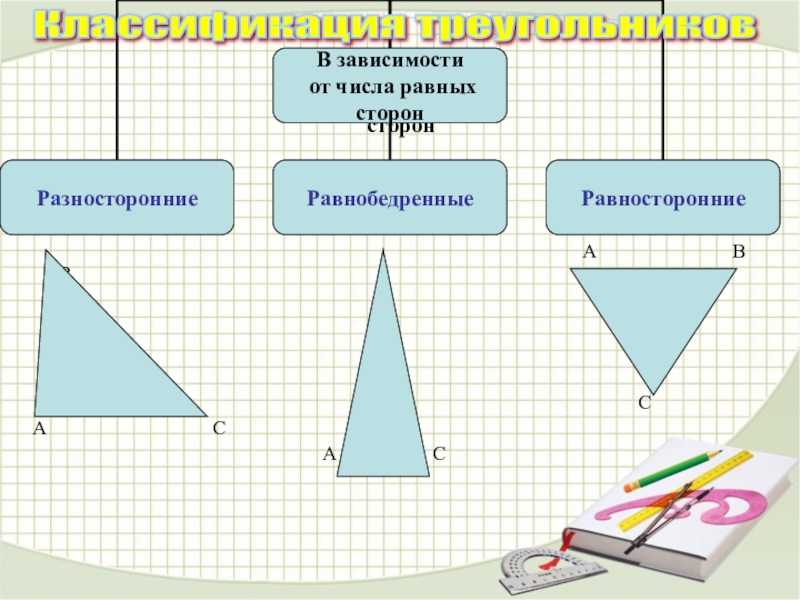
- 8. В зависимости от числа равных сторон
- 9. Треугольник ABC ( рис.23 ) - равнобедренный, если две его стороны равны
- 10. a + b > ca + c
- 11. Высота треугольника – это перпендикуляр, проведенный из вершины
- 12. Жесткость треугольникаТреугольник- фигура жёсткая.Если мы возьмём три
- 13. Электролизный цех УАЗа. г. Каменск-Уральский
- 14. Железнодорожный мостчерез реку Исеть.г. Каменск-Уральский
- 15. Стройка в микрорайоне «Южный». г. Каменск-Уральский
- 16. Мост через р. Сена в Париже
- 17. В аквапарке «Лимпопо»
- 18. В аквапарке «Лимпопо»
- 19. Интересный фактБермудский треугольник — одна из неразгаданных
- 20. Исторический фактЕгипетский треугольник — прямоугольный треугольник с соотношением
- 21. Источники http://1001fact.ru/2012/10/bermudskij-treugolnik-nekotorye-interesnye-fakty/http://school.xvatit.com/index.php?title=Построение_треугольника_с_данными_сторонами._Полные_уроки
- 22. Автор шаблона:Ранько Елена Алексеевна учитель начальных классов МАОУ лицей №21 г. Иваново
Цель Систематизировать и расширить знания о треугольниках
Слайд 1Страна треугольников
Проект выполнили
обучающиеся 7 класса Хвалева Марина, Добривечер Сергей, Дудина
Надежда, Федяева Алена
Руководитель проекта учитель математики Караваева Н.И.
Руководитель проекта учитель математики Караваева Н.И.
Слайд 3Задачи:
изучить исторические сведения о треугольниках;
исследовать геометрические свойства треугольников;
найти информацию о том,
где встречаются треугольники в окружающем нас мире.
Слайд 4Исторические сведения
Треугольник - самая простая замкнутая прямолинейная фигура; одна из
первых, свойства которой человек узнал еще в глубокой древности, так как эта фигура всегда имела широкое применение в практической жизни. В строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей. Изображения треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и в других древних документах. В древней Греции учение о треугольниках развивалось в ионийской школе, основанной в VII в. до н. э. Фалесом, в школе Пифагора и других; оно было затем полностью изложено в первой книге «Начал» Евклида. Понятие о треугольнике исторически развивалось, так: сначала рассматривались лишь правильные, затем равнобедренные и, наконец, разносторонние треугольники.
Фалес Пифагор
640/624 до н. э.624 до н. э. прим. 570 до н. э.
II век до н. э.
Евклид
Слайд 5
ТРЕУГОЛЬНИК
В
С
А
В
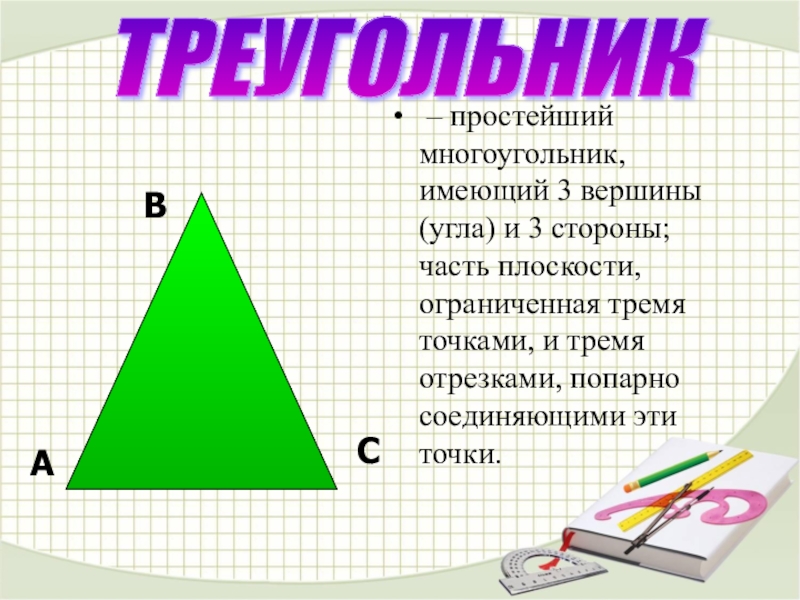
– простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть
плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки.
Слайд 7
Если все три угла острые ( рис.20 ), то это остроугольный треугольник. Если один из углов прямой ( C, рис.21 ), то
это прямоугольный треугольник; стороны a, b, образующие прямой угол, называются катетами; сторона c, противоположная прямому углу, называется гипотенузой. Если один из углов тупой ( B, рис.22 ), то это тупоугольный треугольник.
Слайд 9
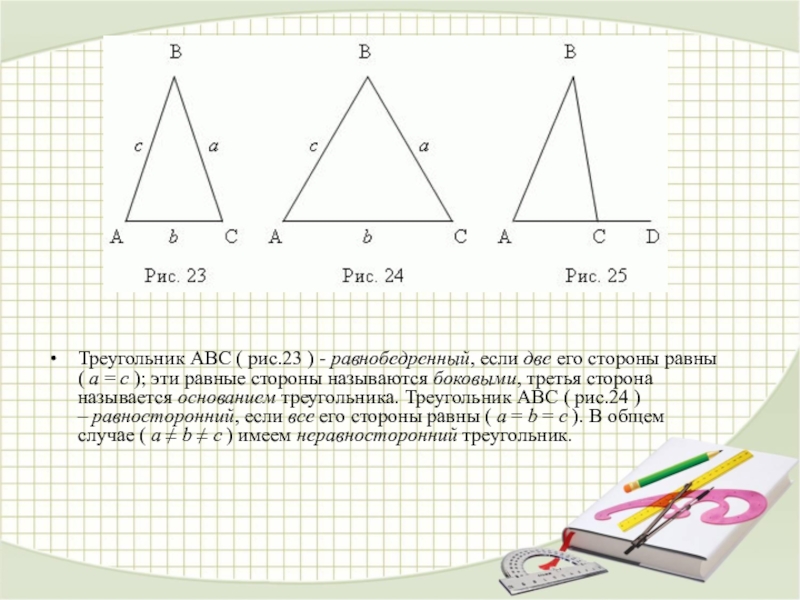
Треугольник ABC ( рис.23 ) - равнобедренный, если две его стороны равны ( a = c ); эти равные стороны
называются боковыми, третья сторона называется основанием треугольника. Треугольник ABC ( рис.24 ) – равносторонний, если все его стороны равны ( a = b = c ). В общем случае ( a ≠ b ≠ c ) имеем неравносторонний треугольник.
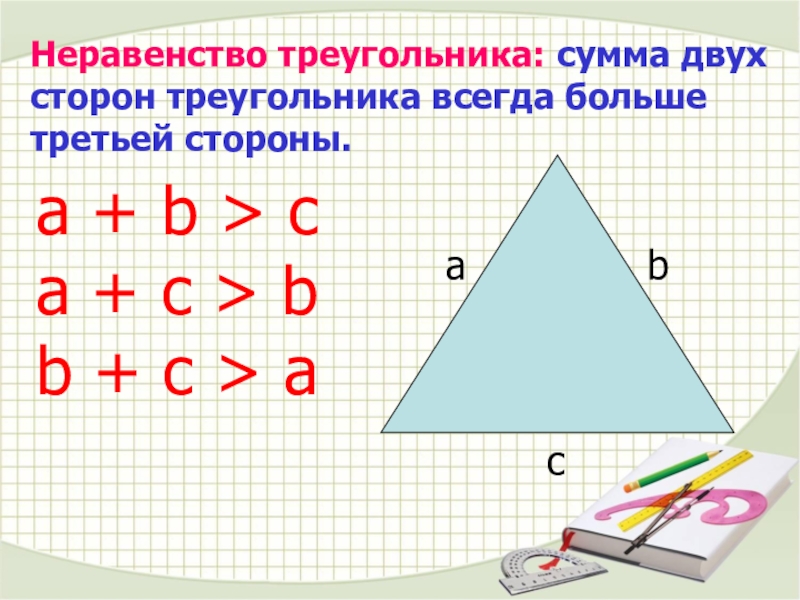
Слайд 10a + b > c
a + c > b
b + c
> a
Неравенство треугольника: сумма двух сторон треугольника всегда больше третьей стороны.
b
a
c
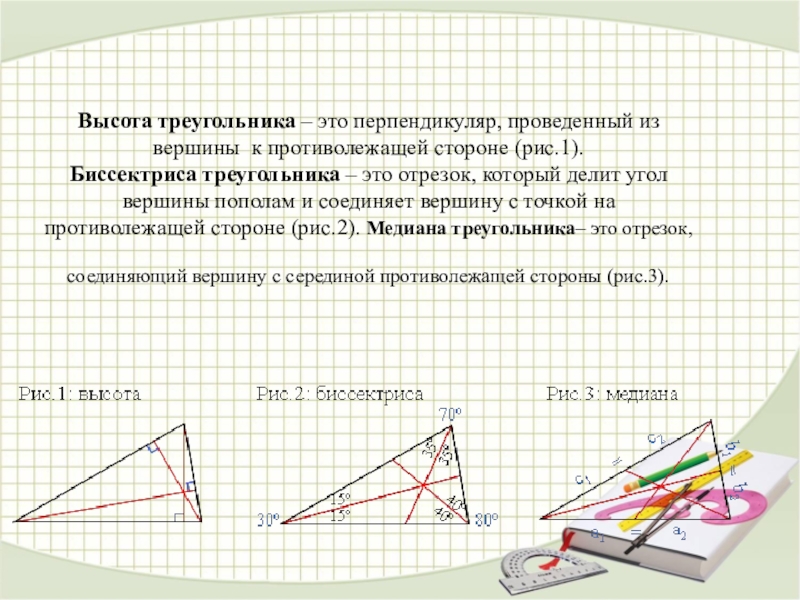
Слайд 11Высота треугольника – это перпендикуляр, проведенный из вершины к противолежащей стороне (рис.1). Биссектриса
треугольника – это отрезок, который делит угол вершины пополам и соединяет вершину с точкой на противолежащей стороне (рис.2). Медиана треугольника– это отрезок, соединяющий вершину с серединой противолежащей стороны (рис.3).
Слайд 12Жесткость треугольника
Треугольник- фигура жёсткая.
Если мы возьмём три металлические или деревянные планки,
закрепим их концы (заклёпками или гвоздями)так, чтобы получился контур треугольника, то увидим, что нам не удастся изменить форму полученного треугольника.
Рассмотрим примеры использования
жёсткости треугольников:
Рассмотрим примеры использования
жёсткости треугольников:
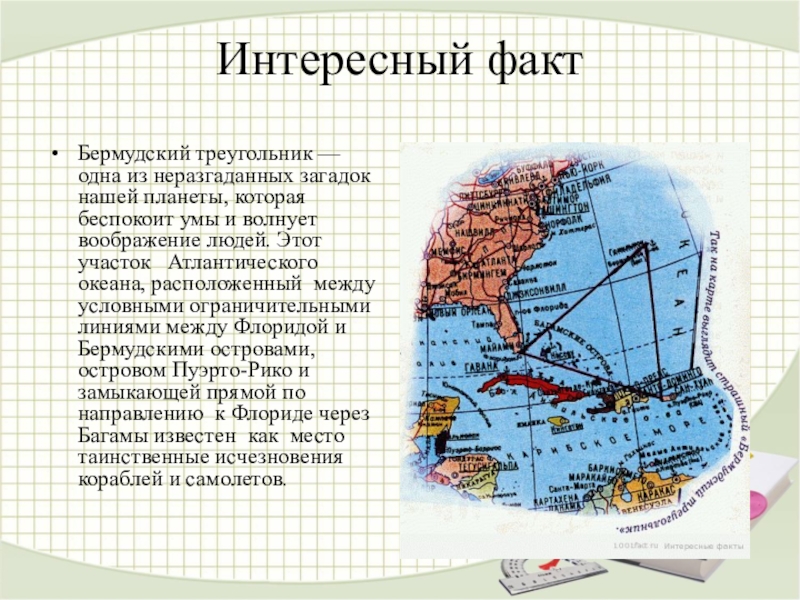
Слайд 19Интересный факт
Бермудский треугольник — одна из неразгаданных загадок нашей планеты, которая
беспокоит умы и волнует воображение людей. Этот участок Атлантического океана, расположенный между условными ограничительными линиями между Флоридой и Бермудскими островами, островом Пуэрто-Рико и замыкающей прямой по направлению к Флориде через Багамы известен как место таинственные исчезновения кораблей и самолетов.
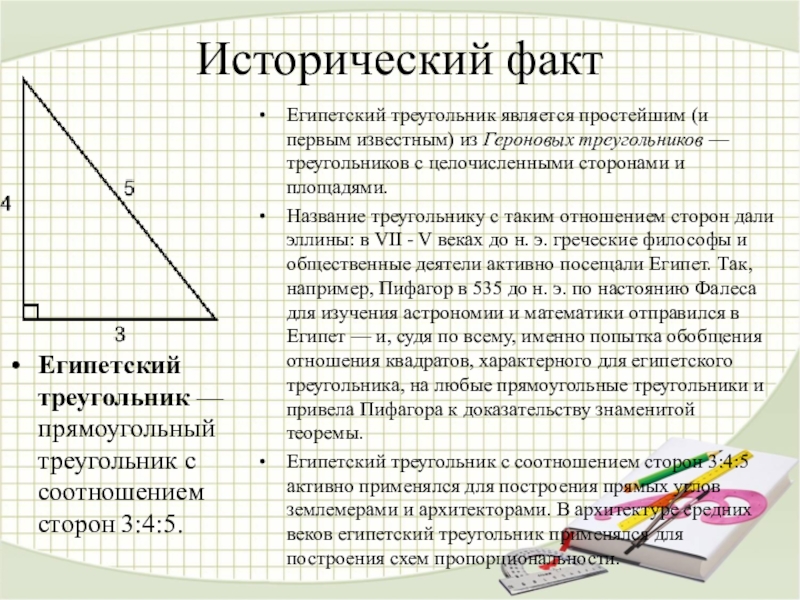
Слайд 20Исторический факт
Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.
Египетский треугольник
является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.
Название треугольнику с таким отношением сторон дали эллины: в VII - V веках до н. э. греческие философы и общественные деятели активно посещали Египет. Так, например, Пифагор в 535 до н. э. по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к доказательству знаменитой теоремы.
Египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов землемерами и архитекторами. В архитектуре средних веков египетский треугольник применялся для построения схем пропорциональности.
Название треугольнику с таким отношением сторон дали эллины: в VII - V веках до н. э. греческие философы и общественные деятели активно посещали Египет. Так, например, Пифагор в 535 до н. э. по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к доказательству знаменитой теоремы.
Египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов землемерами и архитекторами. В архитектуре средних веков египетский треугольник применялся для построения схем пропорциональности.