окружности
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Вписанная и описанная окружность
Содержание
- 1. Презентация по геометрии Вписанная и описанная окружность
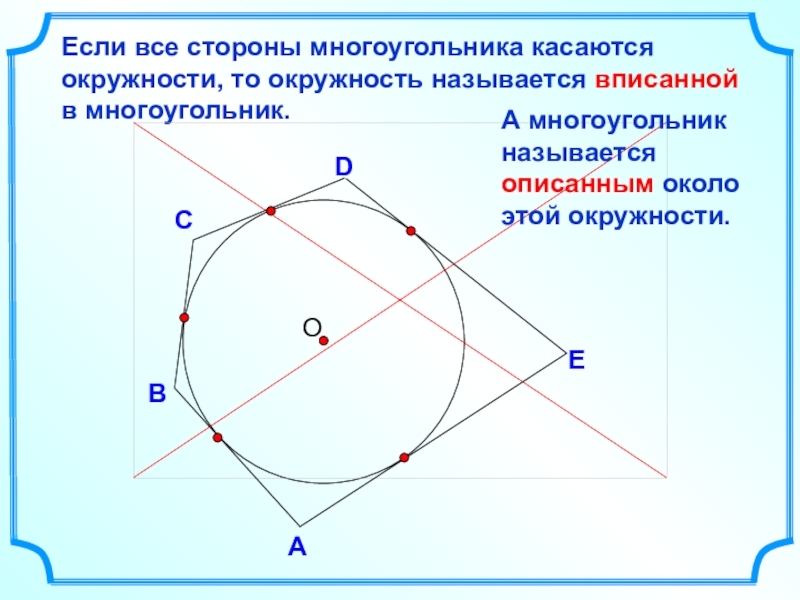
- 2. DВСЕсли все стороны многоугольника касаются окружности, то
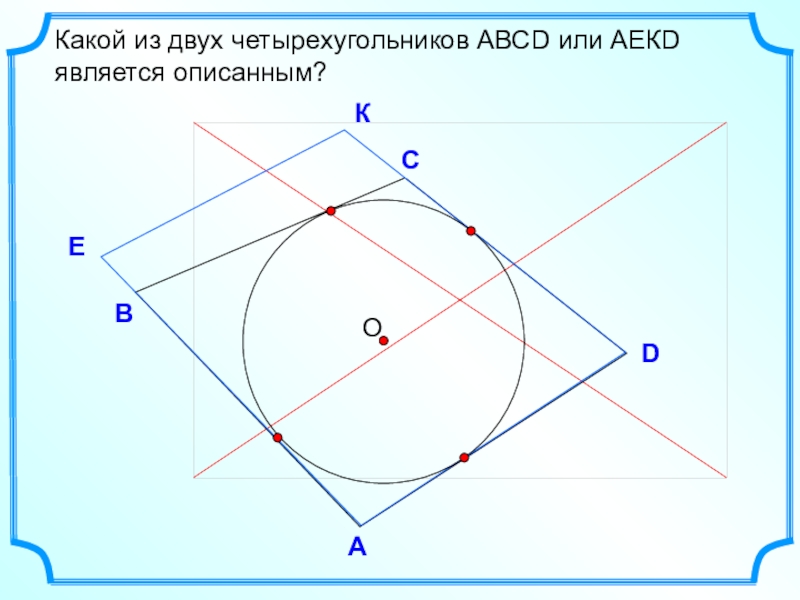
- 3. DВСКакой из двух четырехугольников АВСD или АЕКD является описанным?АEК
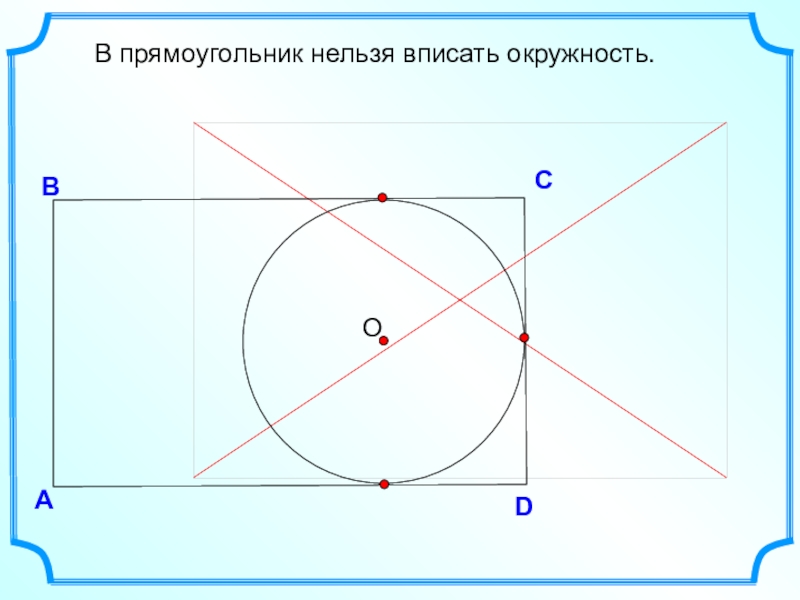
- 4. DВСВ прямоугольник нельзя вписать окружность.А
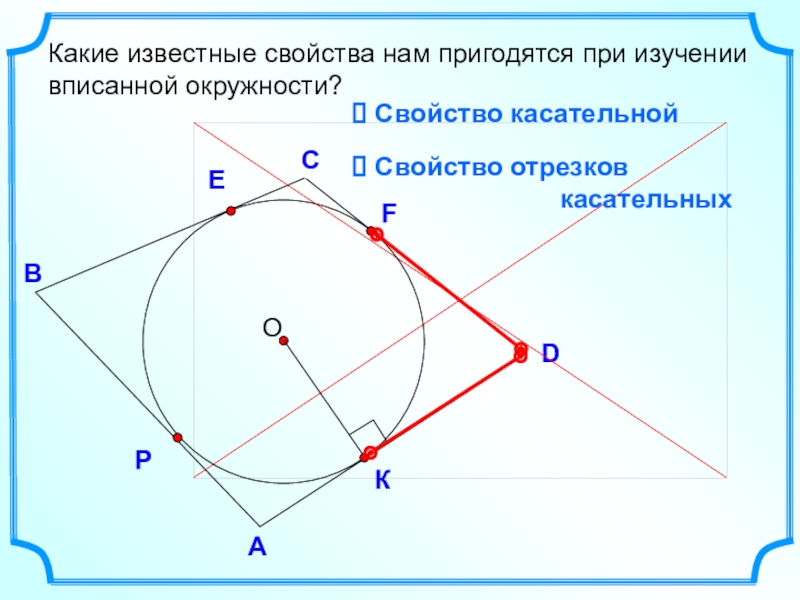
- 5. DВСКакие известные свойства нам пригодятся при изучении
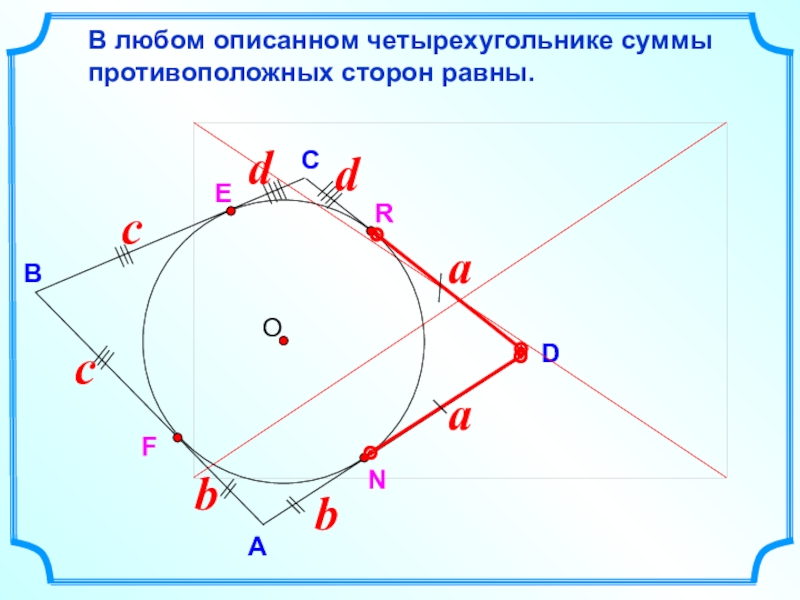
- 6. DВСВ любом описанном четырехугольнике суммы противоположных сторон равны.АERNF
- 7. DВС
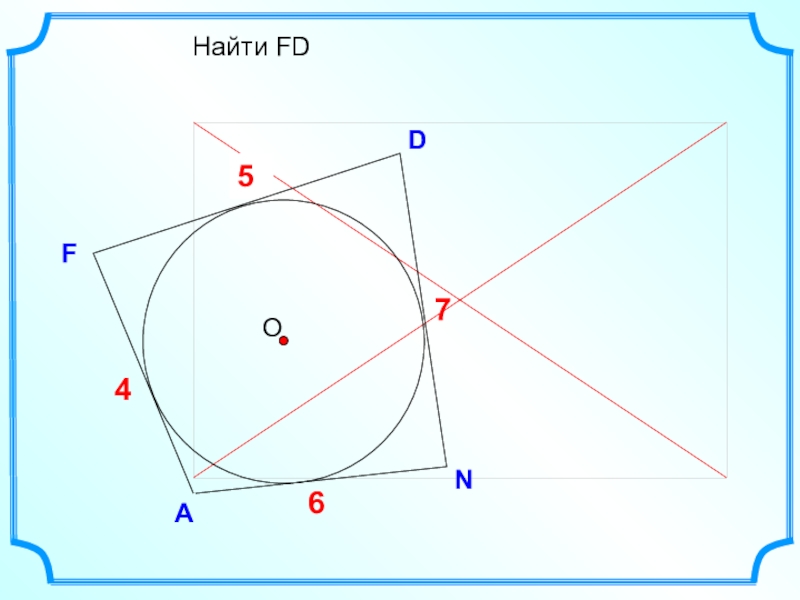
- 8. D F Найти FDАN?4765
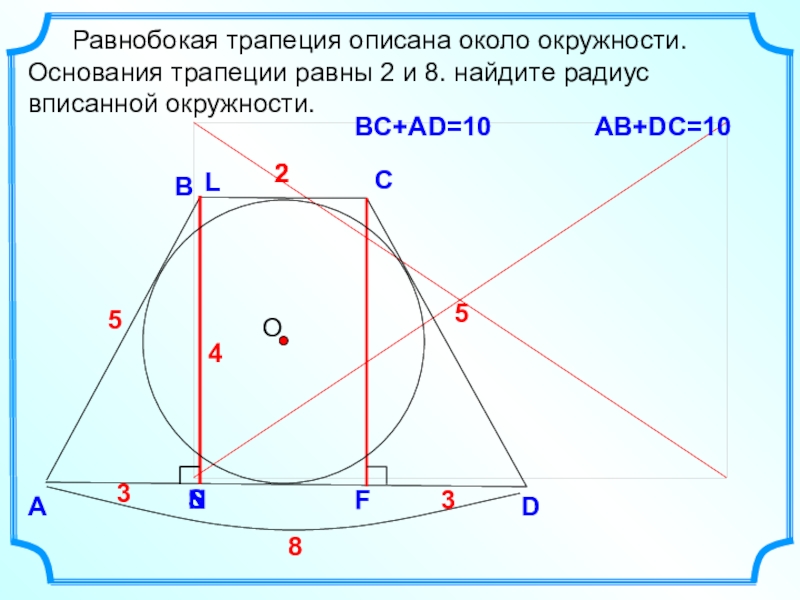
- 9. DВС Равнобокая трапеция описана около
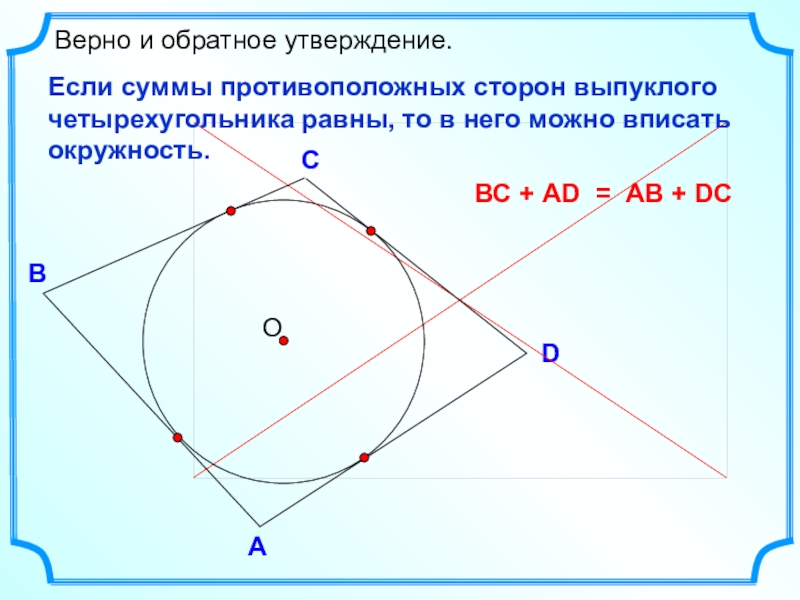
- 10. DВСВерно и обратное утверждение.АЕсли суммы противоположных сторон
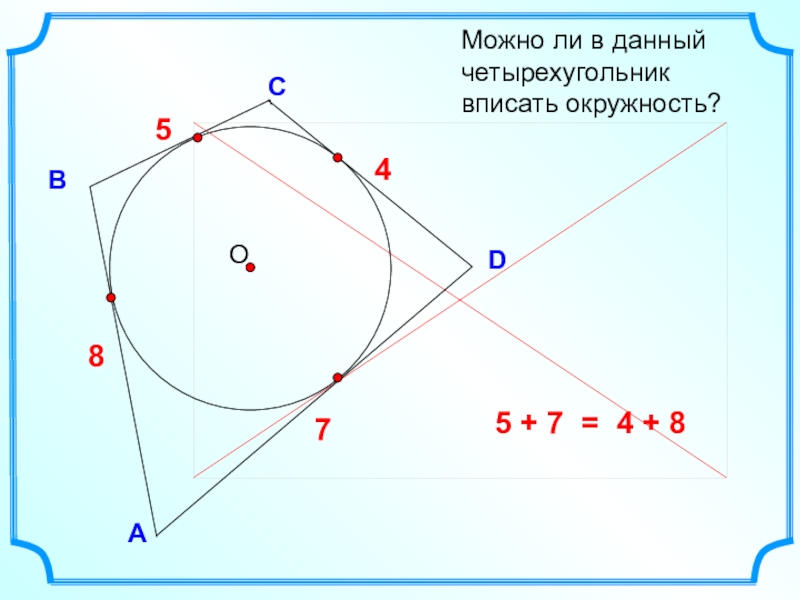
- 11. DВСМожно ли в данный четырехугольник вписать окружность?А5 + 7 = 4 + 85748
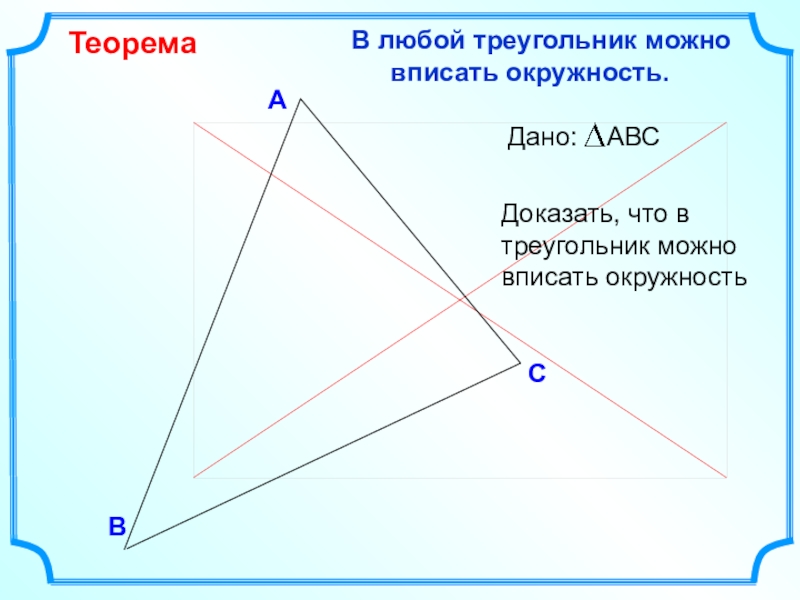
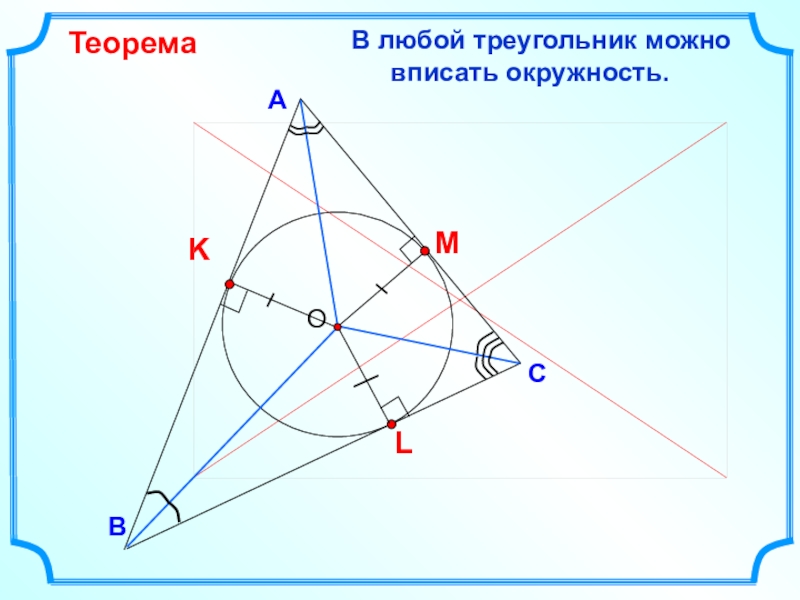
- 12. ВСА В любой треугольник можно вписать окружность.ТеоремаДоказать, что в треугольник можно вписать окружность
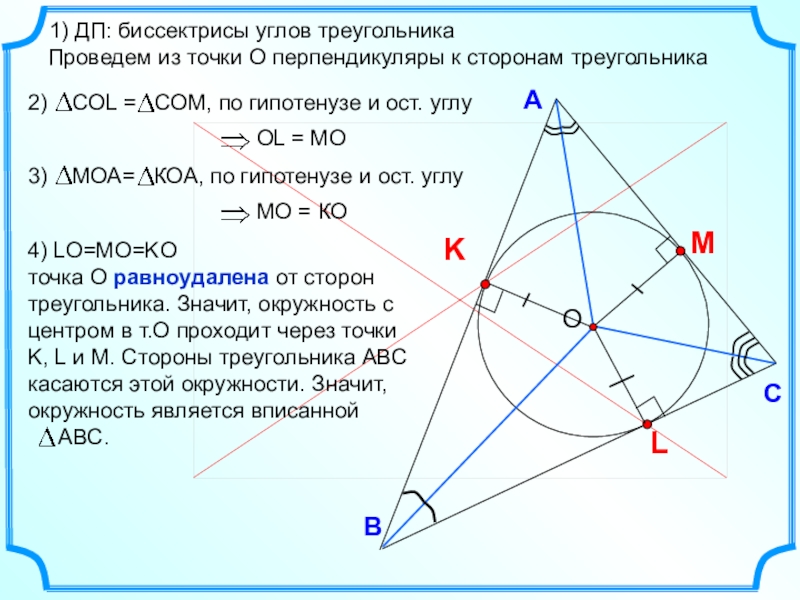
- 13. ВСА1) ДП: биссектрисы углов треугольникаПроведем из точки О перпендикуляры к сторонам треугольника
- 14. ВСА В любой треугольник можно вписать окружность.Теорема
- 15. DВС
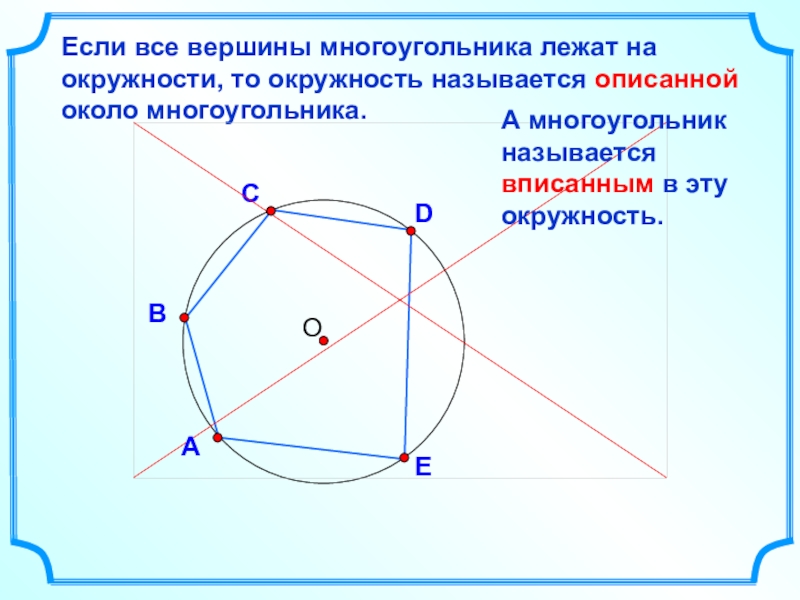
- 16. DВСЕсли все вершины многоугольника лежат на окружности,
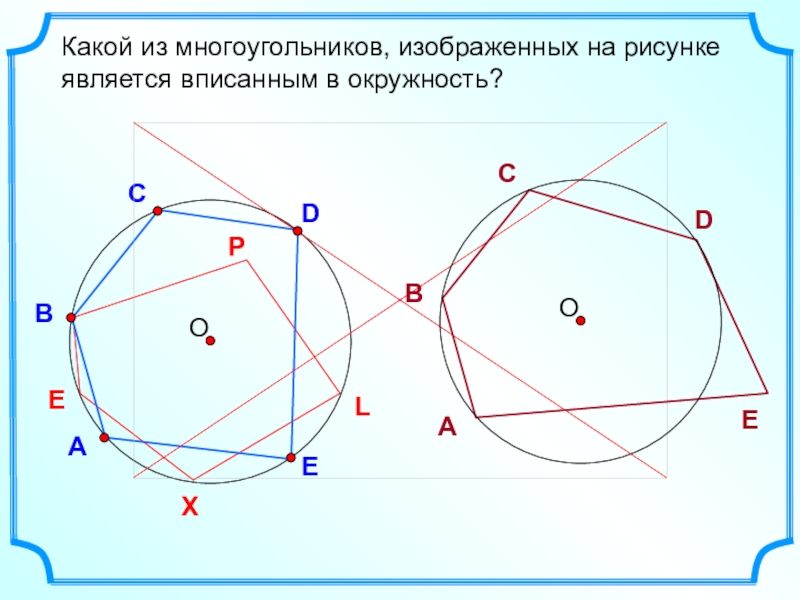
- 17. DВСКакой из многоугольников, изображенных на рисунке является вписанным в окружность?АELPXE
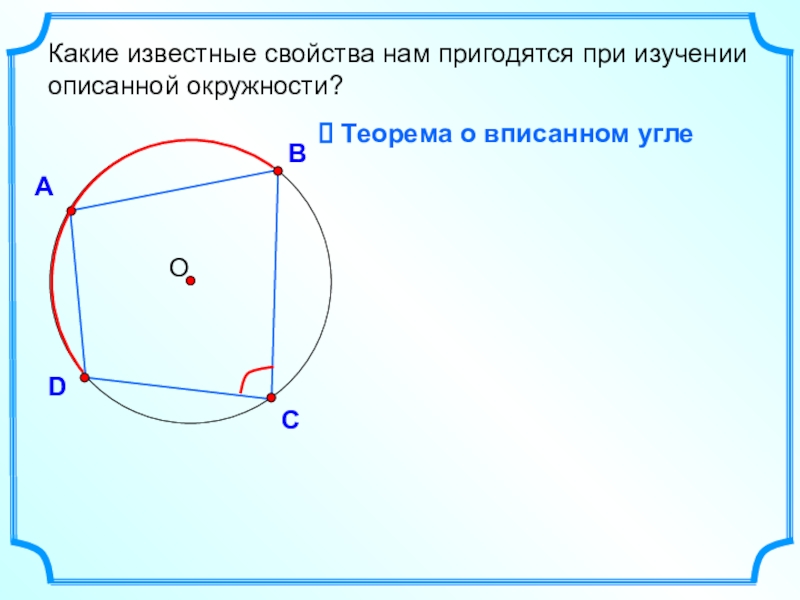
- 18. АВDСКакие известные свойства нам пригодятся при изучении описанной окружности? Теорема о вписанном угле
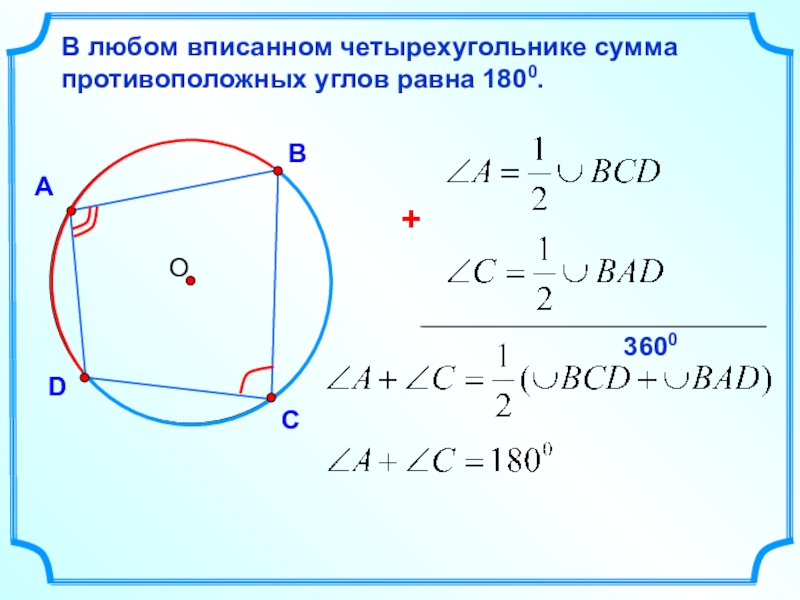
- 19. АВDВ любом вписанном четырехугольнике сумма противоположных углов равна 1800.С3600
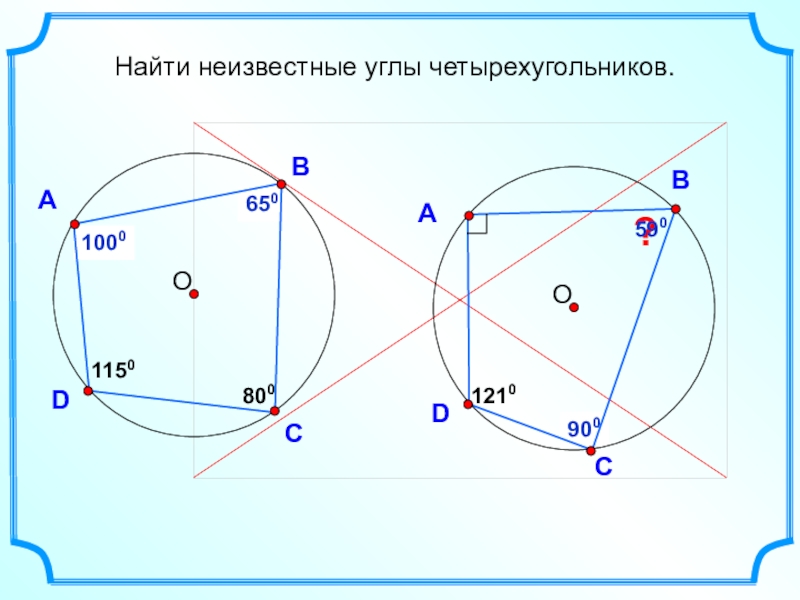
- 20. ?590?900?650?1000DАВС8001150DАВС1210Найти неизвестные углы четырехугольников.
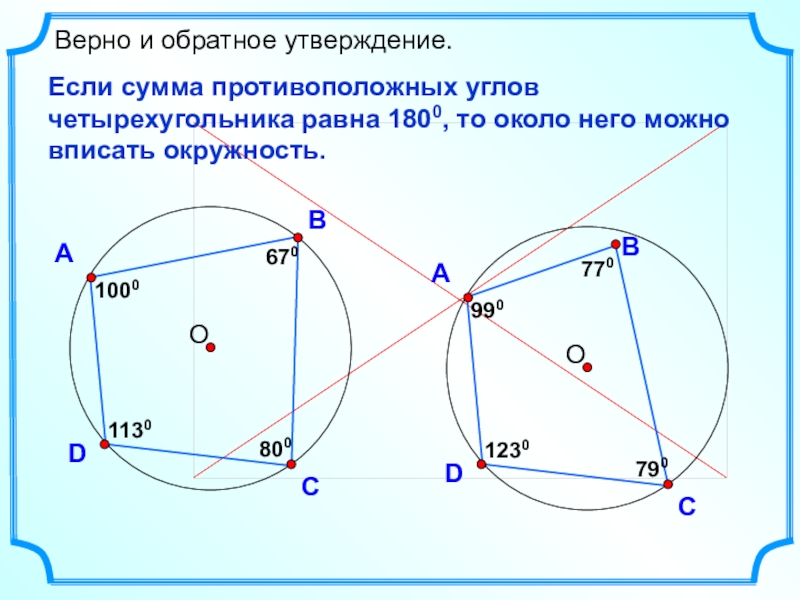
- 21. DВерно и обратное утверждение.Если сумма противоположных углов четырехугольника равна 1800, то около него можно вписать окружность.АВС80010001130670
- 22. ВСА
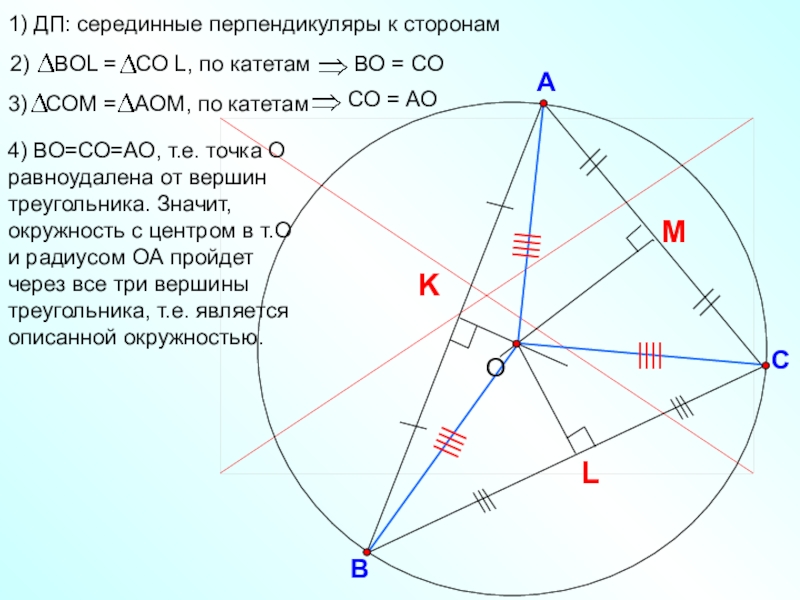
- 23. ВСА1) ДП: серединные перпендикуляры к сторонам4) ВО=СО=АО,
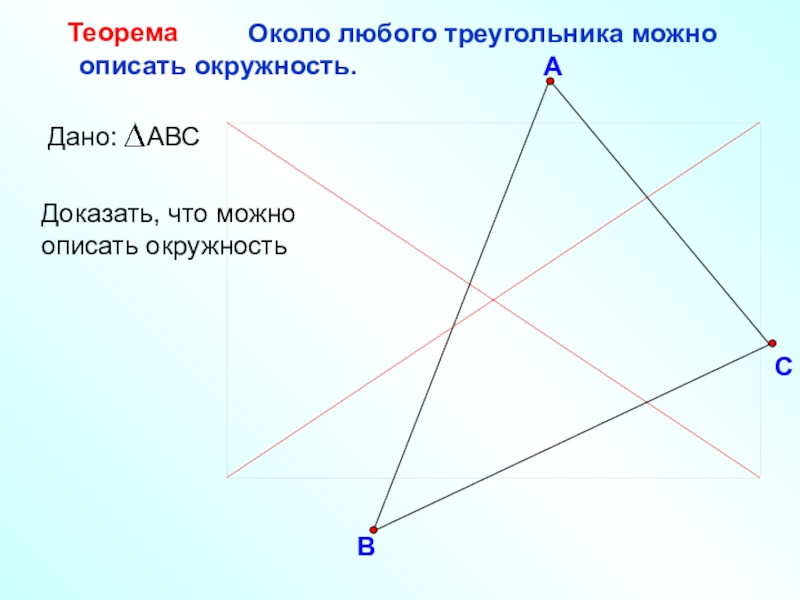
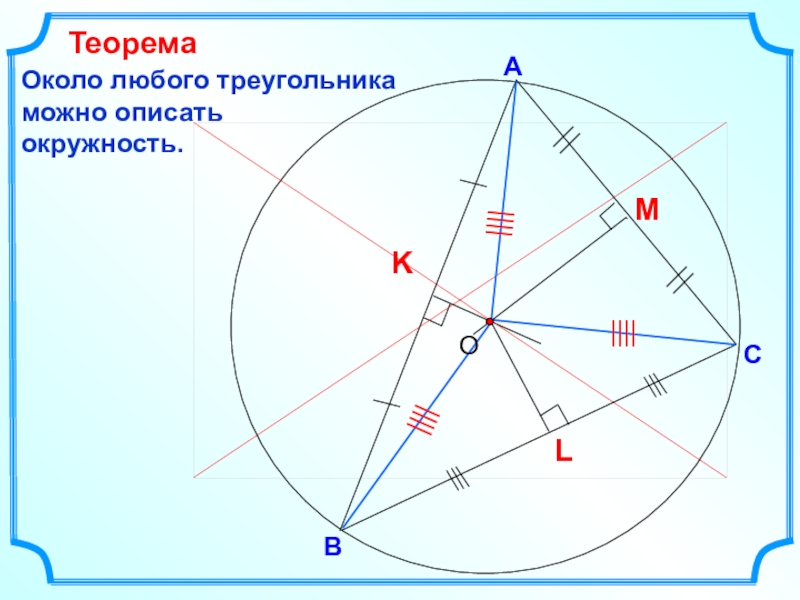
- 24. ВСАОколо любого треугольника можно описать окружность.Теорема
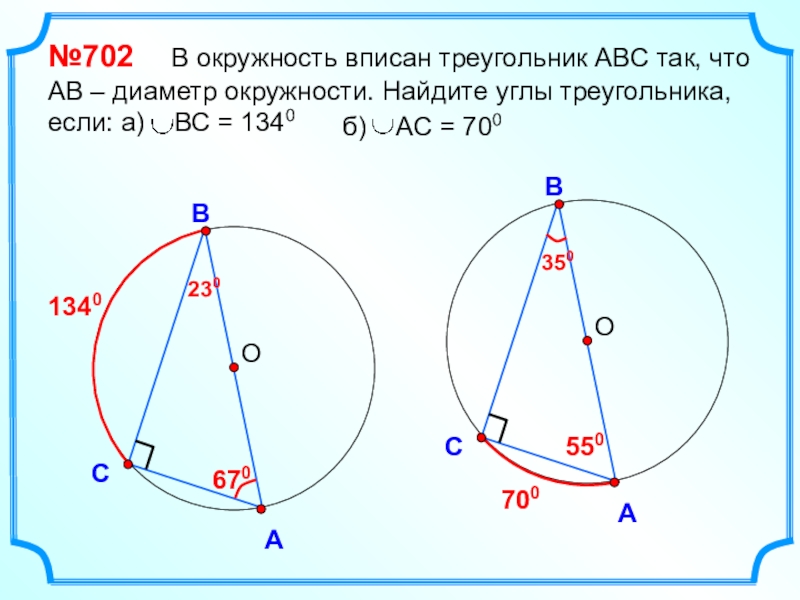
- 25. ОВСА№702 В окружность вписан треугольник
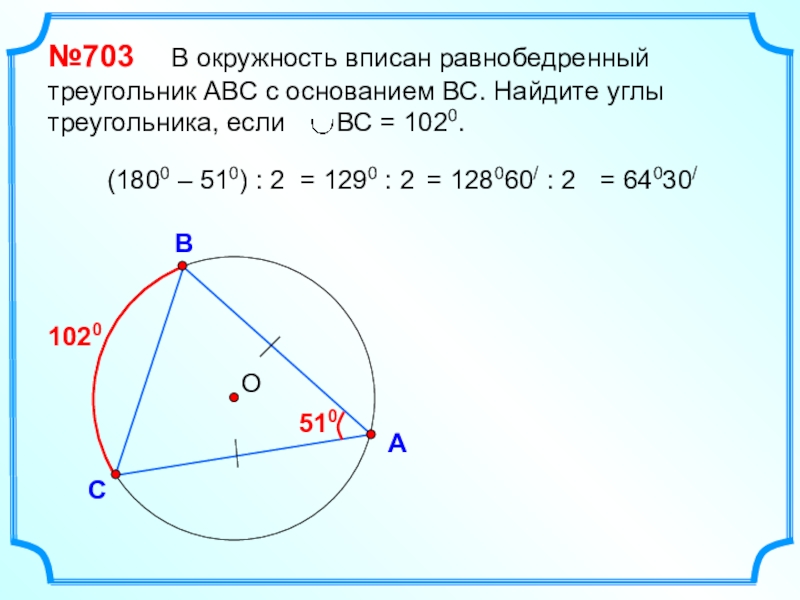
- 26. ОВСА№703 В окружность вписан равнобедренный
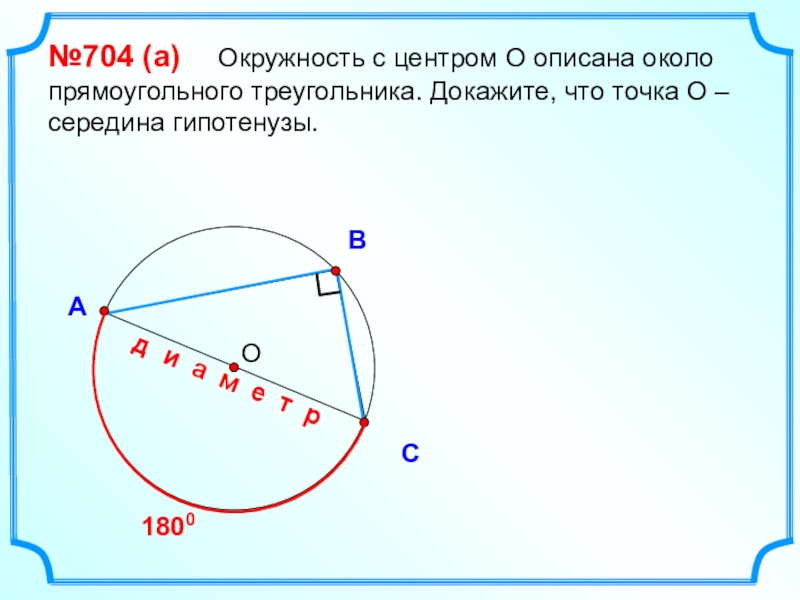
- 27. ВСА№704 (a) Окружность с центром
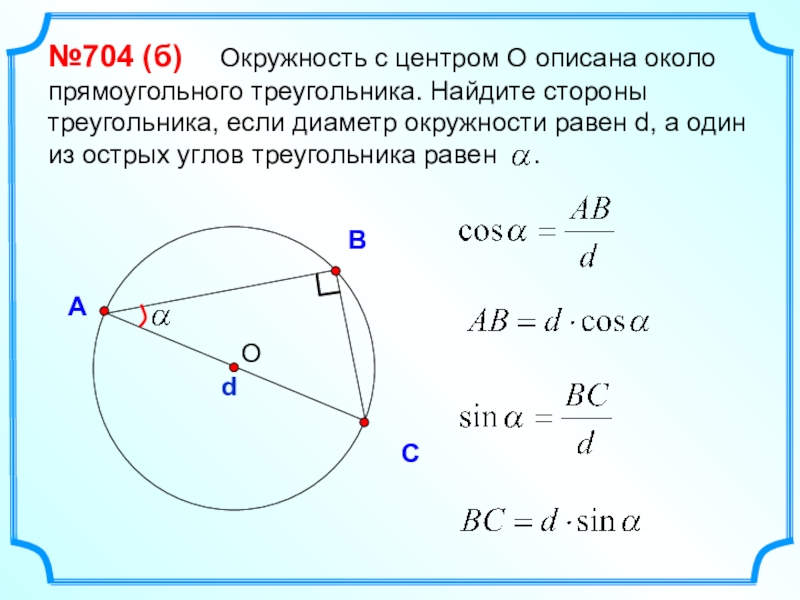
- 28. ВСА№704 (б) Окружность с центром
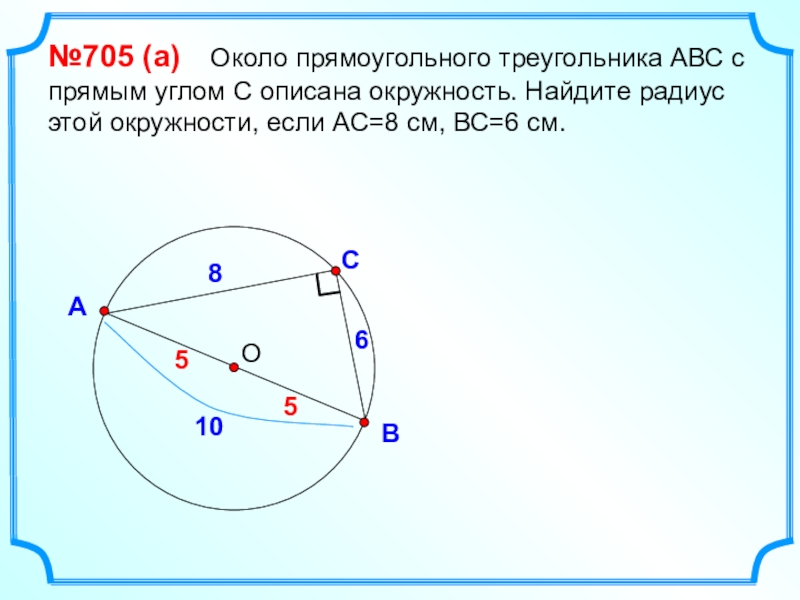
- 29. СВА№705 (а) Около прямоугольного треугольника АВС
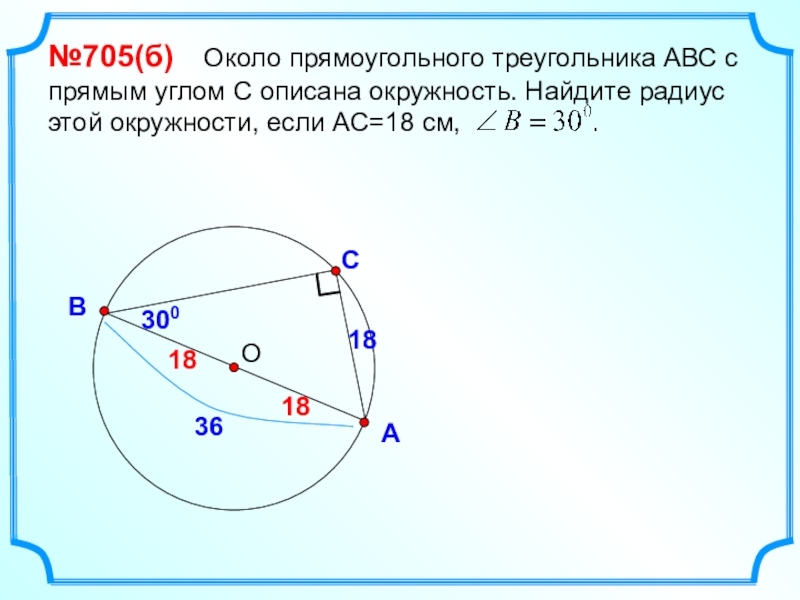
- 30. САВ№705(б) Около прямоугольного треугольника АВС с
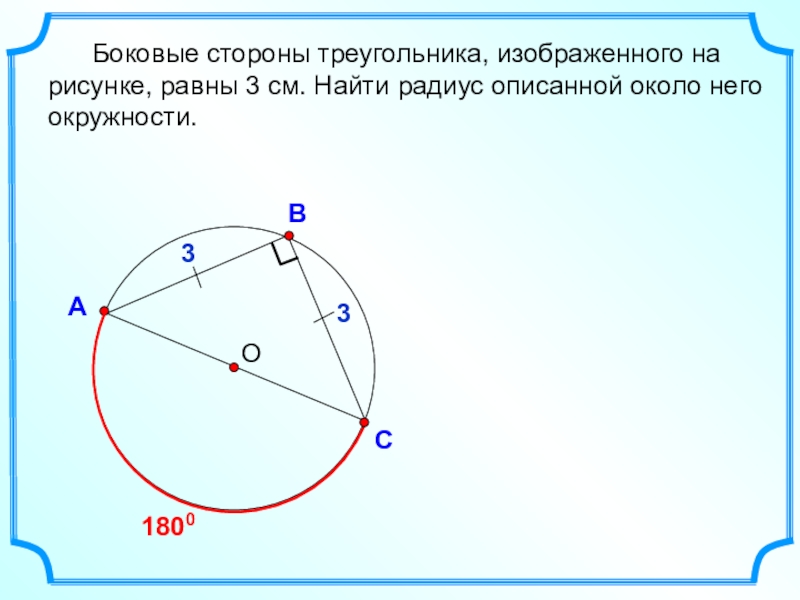
- 31. ОВСА Боковые стороны треугольника, изображенного
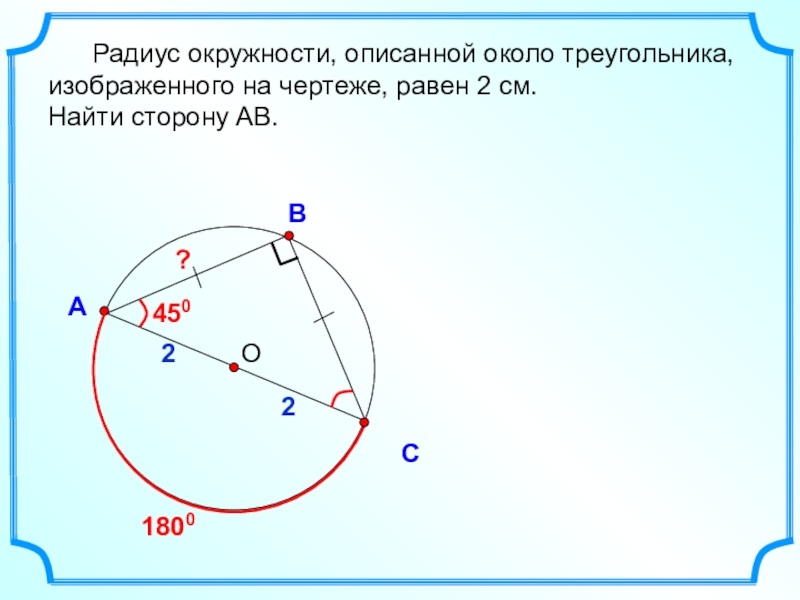
- 32. ОВСА Радиус окружности, описанной около
Слайд 2D
В
С
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в
А
E
А многоугольник называется описанным около этой окружности.
Слайд 5D
В
С
Какие известные свойства нам пригодятся при изучении вписанной окружности?
А
E
Свойство касательной
касательных
F
P
Слайд 7D
В
С
Сумма
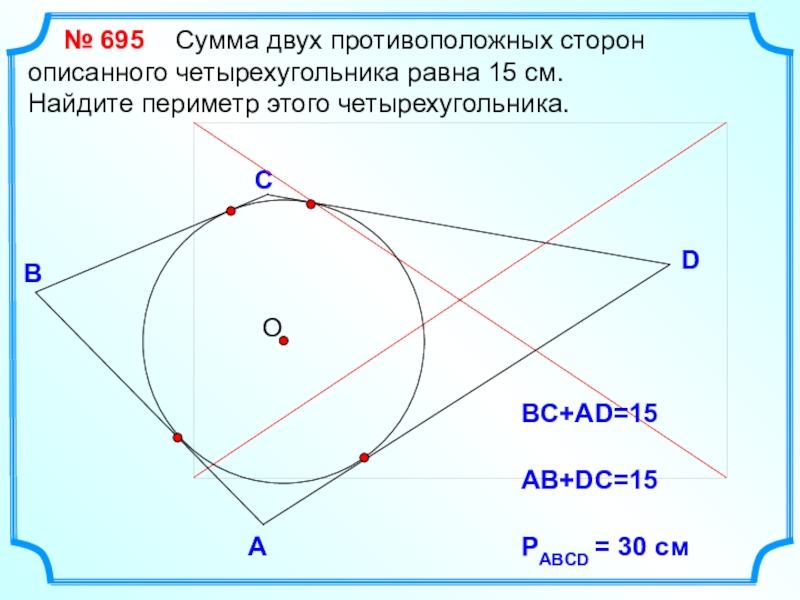
Найдите периметр этого четырехугольника.
А
№ 695
ВC+AD=15
AB+DC=15
PABCD = 30 см
Слайд 9D
В
С
Равнобокая трапеция описана около окружности. Основания трапеции равны
А
ВC+AD=10
AB+DC=10
2
8
2
4
Слайд 10D
В
С
Верно и обратное утверждение.
А
Если суммы противоположных сторон выпуклого четырехугольника равны, то
ВС + АD = АВ + DC
Слайд 12В
С
А
В любой треугольник можно вписать окружность.
Теорема
Доказать, что в треугольник
Слайд 13В
С
А
1) ДП: биссектрисы углов треугольника
Проведем из точки О перпендикуляры к сторонам
Слайд 15
D
В
С
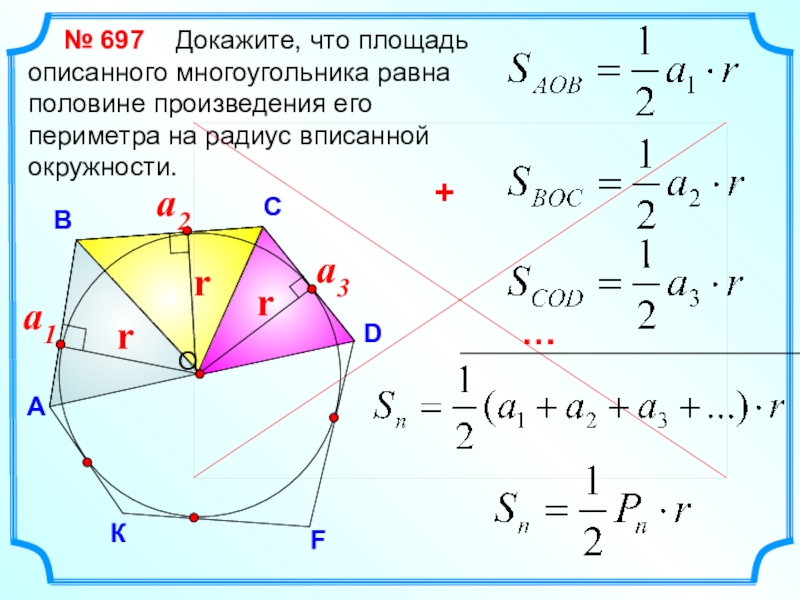
Докажите,
А
№ 697
F
a1
a2
a3
…
К
Слайд 16
D
В
С
Если все вершины многоугольника лежат на окружности, то окружность называется описанной
А
E
А многоугольник называется вписанным в эту окружность.
Слайд 18
А
В
D
С
Какие известные свойства нам пригодятся при изучении описанной окружности?
Теорема о
Слайд 21D
Верно и обратное утверждение.
Если сумма противоположных углов четырехугольника равна 1800, то
А
В
С
800
1000
1130
670
Слайд 22В
С
А
описать окружность.
Теорема
Доказать, что можно описать окружность
Слайд 23В
С
А
1) ДП: серединные перпендикуляры к сторонам
4) ВО=СО=АО, т.е. точка О равноудалена
Слайд 25
О
В
С
А
№702 В окружность вписан треугольник АВС так, что АВ
1340
670
230
700
550
350
Слайд 26
О
В
С
А
№703 В окружность вписан равнобедренный треугольник АВС с основанием
1020
510
(1800 – 510) : 2
= 1290 : 2
= 128060/ : 2
= 64030/
Слайд 27
В
С
А
№704 (a) Окружность с центром О описана около прямоугольного
1800
д и а м е т р
Слайд 28
В
С
А
№704 (б) Окружность с центром О описана около прямоугольного
d
Слайд 29
С
В
А
№705 (а) Около прямоугольного треугольника АВС с прямым углом С
8
6
Слайд 30
С
А
В
№705(б) Около прямоугольного треугольника АВС с прямым углом С описана
18
300
Слайд 31
О
В
С
А
Боковые стороны треугольника, изображенного на рисунке, равны 3
1800
3
3
Слайд 32
О
В
С
А
Радиус окружности, описанной около треугольника, изображенного на чертеже,
Найти сторону АВ.
1800
2
2
450
?