- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Теория обучения геометрии: Методико -педагогическое сопровождение урока. Модель.
Содержание
- 1. Теория обучения геометрии: Методико -педагогическое сопровождение урока. Модель.
- 2. Цели обучения геометрии в школеВыделяются два основных
- 3. Слайд 3
- 4. Э л е м е н т
- 5. В качестве примера рассмотрим задачу по теме
- 6. Лабораторные работыI. Планиметрия 1. Построение геометрических мест
- 7. Лабораторные работыII. Стереометрия 1. Изображение пространственных фигур
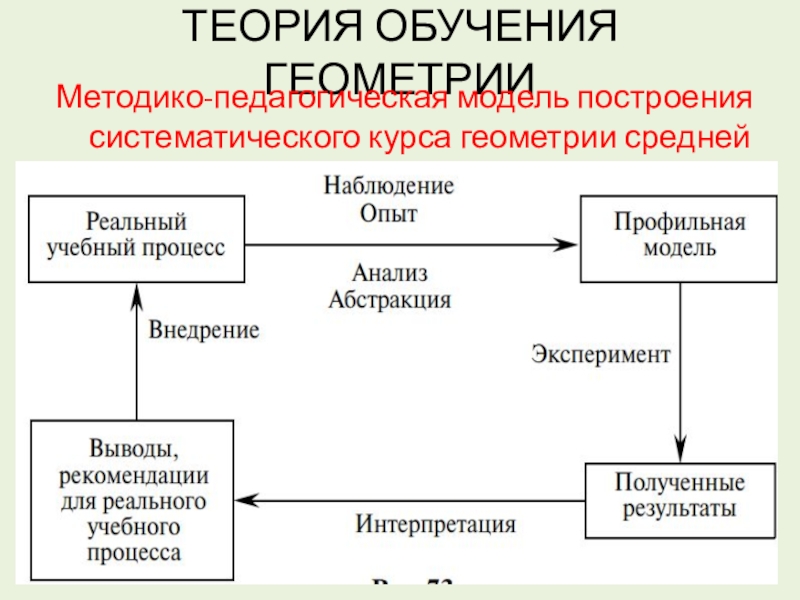
Слайд 1ТЕОРИЯ ОБУЧЕНИЯ ГЕОМЕТРИИ
Методико-педагогическая модель построения систематического курса геометрии средней школы
Слайд 2Цели обучения геометрии в школе
Выделяются два основных направления в постановке курса
В соответствии с этим определяются следующие ц е л и обучения математике в школе:
а) овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
б) интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;
в) формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
г) формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
Слайд 4Э л е м е н т ы с о д
1. Термины (их запись, чтение, обозначение); понятия (не определяемые и определяемые).
2. Аксиомы, теоремы, задачи (среди которых мы выделяем устные, основные (базовые, стандартные), повышенной трудности, нестандартные, исследовательские, прикладные и практические, занимательные, исторические).
3. Классификации.
4. Теории.
5. Факты (исторические справки, дополнительные сведения).
Слайд 5В качестве примера рассмотрим задачу по теме «Четырехугольники» курса геометрии основной
1. Уровень выравнивания. Докажите, что середины сторон (выпуклого) четырехугольника являются вершинами параллелограмма. Докажите, что площадь полученного параллелограмма равна половине площади данного четырехугольника. Указание. Для решения задачи проведите какую-нибудь диагональ данного четырехугольника и рассмотрите образовавшиеся треугольники.
2. Базовый, основной уровень. Какой четырехугольник получится, если последовательно соединить середины сторон (выпуклого) четырехугольника? Найдите площадь получившегося четырехугольника, если площадь данного четырехугольника равна 16 см2.
3. Продвинутый уровень. Какой четырехугольник получится, если последовательно соединить середины сторон (выпуклого) четырехугольника? Найдите площадь получившегося четырехугольника, если площадь данного четырехугольника равна Q. В каком случае полученный четырехугольник будет: а) параллелограммом; б) прямоугольником; в) ромбом; г) квадратом?
4. Творческий уровень. Докажите, что точка пересечения отрезков, соединяющих середины противоположных сторон (выпуклого) четырехугольника, делит пополам отрезок, соединяющий середины диагоналей этого четырехугольника.
Слайд 6Лабораторные работы
I. Планиметрия
1. Построение геометрических мест точек.
2. Построение кривых:
3. Получение циклоидальных кривых: циклоиды, кардиоиды, астроиды.
4. Центральная симметрия.
5. Поворот.
6. Осевая симметрия.
7. Параллельный перенос.
8. Заполнение плоскости: равными четырехугольниками, правильными многоугольниками.
9. Задачи на разрезание (на плоскости).
10. Вычисление площадей плоских фигур.
Слайд 7Лабораторные работы
II. Стереометрия
1. Изображение пространственных фигур на плоскости.
2. Моделирование
3. Опыты с листом Мебиуса.
4. Каскадные модели последовательно вписанных друг в друга правильных многогранников.
5. Стереометрические фигуры из куска бумаги.
6. Заполнение пространства многогранниками
7. Задачи на разрезание (в пространстве).
8. Фигуры вращения.
9. Вычисление площади поверхности фигур вращения.
10. Вычисление объема фигур вращения.