- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Теоремы: Признаки равенства треугольников
Содержание
- 1. Теоремы: Признаки равенства треугольников
- 2. Первые упоминания о фигуре были обнаружены на
- 3. После упадка математики в Древней Греции её
- 4. Столь большая заинтересованность к треугольнику и в
- 5. Треугольник является одной из ключевых и самых
- 6. Существует всего 3 признака равенства треугольников: первый,
- 7. ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВТЕОРЕМА:
- 8. ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВТЕОРЕМА: Если сторона
- 9. ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВТЕОРЕМА: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
- 10. ДОКАЗАТЕЛЬСТВА ТЕОРЕМ: первый признак рав-ва
- 11. ДОКАЗАТЕЛЬСТВА ТЕОРЕМ первый признак рав-ва
- 12. ДОКАЗАТЕЛЬСТВА ТЕОРЕМ первый признак рав-ва Рассмотрим
- 13. ДОКАЗАТЕЛЬСТВА ТЕОРЕМ второй признак рав-ва
- 14. ДОКАЗАТЕЛЬСТВА ТЕОРЕМ второй признак рав-ва
- 15. ДОКАЗАТЕЛЬСТВА ТЕОРЕМ третий признак рав-ва
- 16. СПАСИБО ЗА ВНИМАНИЕ!!!
Первые упоминания о фигуре были обнаружены на папирусах Древнего Египта (тут стоит отметить, что некоторым из них уже более 4000 лет). Затем большое внимание к треугольнику проявляли древние Греки: создание теоремы Пифагора и формула Герона. К
Слайд 2Первые упоминания о фигуре были обнаружены на папирусах Древнего Египта (тут
стоит отметить, что некоторым из них уже более 4000 лет). Затем большое внимание к треугольнику проявляли древние Греки: создание теоремы Пифагора и формула Герона. К слову эти открытия были сделаны примерно 2000 лет назад. Самый известный математик древности – Пифагор черпал информацию у египтян. Без полученных там знаний он бы не смог создать свою великую теорему, например египтянам было известно о том, что треугольник со сторонами 3, 4, 5 всегда будет являться прямоугольным – основа теоремы Пифагора.
Слайд 3После упадка математики в Древней Греции её центр переместился в Индию,
где были проведены тысячи исследований, которые также касались треугольника. Как ни странно, но после стольких открытий заинтересованность к треугольнику спала, и новая волна изучения данной фигуры пришла только в 15-16 веках. Именно в это время у треугольника появилось подавляющее количество признаков и свойств, начал развиваться раздел планиметрии под названием «Новая геометрия треугольника».
Слайд 4Столь большая заинтересованность к треугольнику и в целом к геометрии объясняется
тем, что математические знания были нужны в навигации и военном деле. Все открытия той эпохи помогают людям и несут хорошую службу до сих пор. К слову в то время огромный вклад в изучении треугольника внес русский, написавший труд «Новое начало геометрии».
Слайд 5Треугольник является одной из ключевых и самых важных и самых изученных
фигур в мире, несмотря на это его изучение продолжается множеством ученых до настоящего времени и закончится еще не скоро. Свойства и признаки, которые находят у треугольника, активно применяются во всех сферах жизни человека и областях промышленности, а законы, открытые несколько тысяч лет назад, никогда не устаревают и являются вечными
Слайд 6Существует всего 3 признака равенства треугольников: первый, второй и третий. Все
эти признаки ввёл в геометрию известный математик Пифагор. Его имя не мало встречается в учебниках математики.
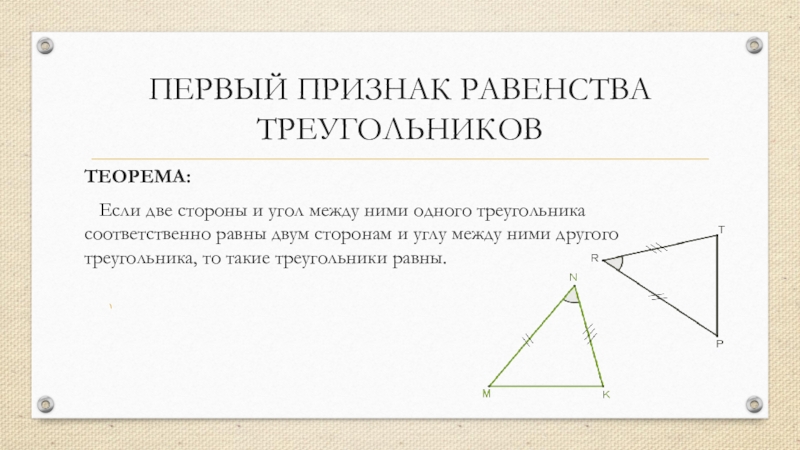
Слайд 7ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
ТЕОРЕМА:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Слайд 8ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
ТЕОРЕМА:
Если сторона и два прилежащих к
ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Слайд 9ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
ТЕОРЕМА:
Если три стороны одного треугольника соответственно равны трем
сторонам другого треугольника, то такие треугольники равны.
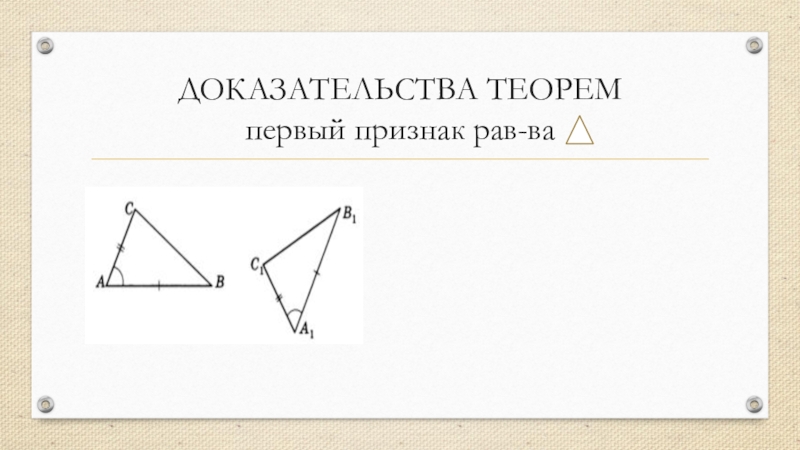
Слайд 12ДОКАЗАТЕЛЬСТВА ТЕОРЕМ
первый признак рав-ва
Рассмотрим треугольники ABC и A1B1C1, у
которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1. Докажем, что Δ ABC = Δ A1B1C1.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
Ч.т.д.
Так как ∠ А = ∠ А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.
Ч.т.д.