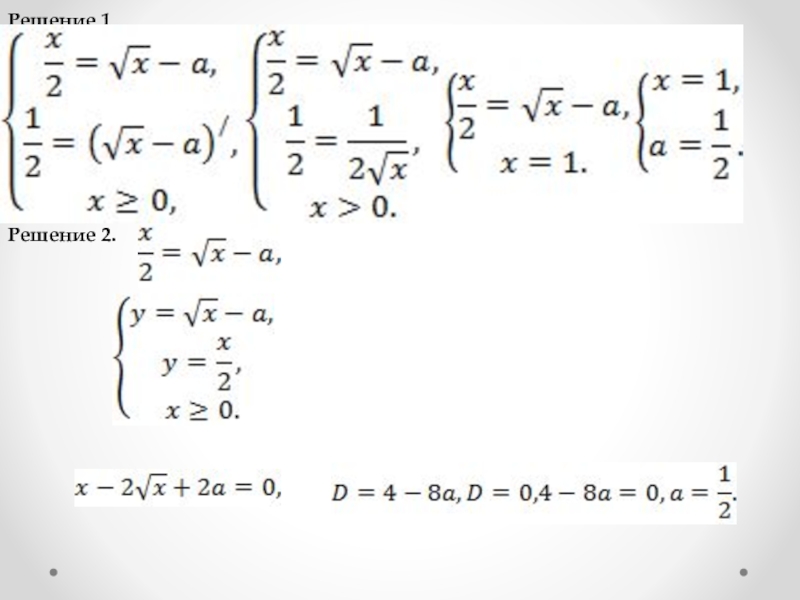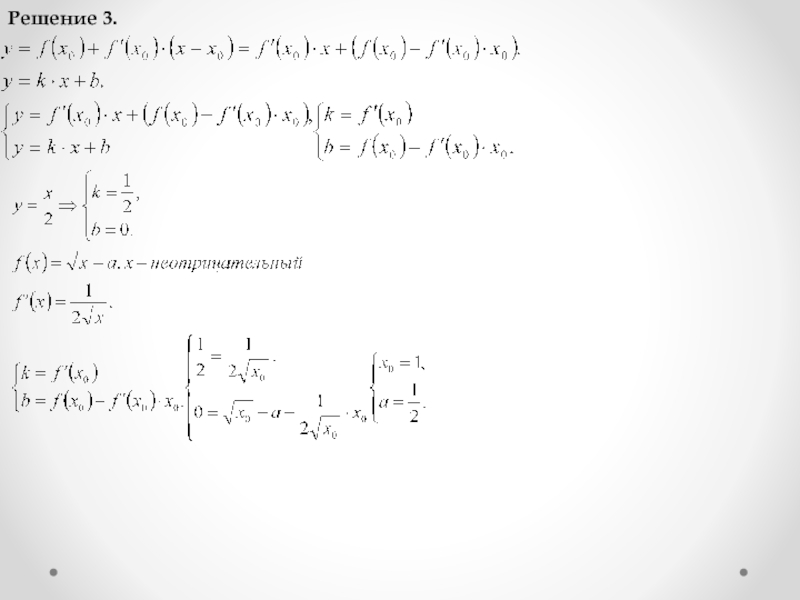Слайд 1«Каждый человек меня в чем-то превосходит;
и в этом смысле мне есть
чему у него поучиться»
Эмерсон Ральф
Мастер-класс:
«Раздел планиметрии в содержании ОГЭ и ЕГЭ»»
Постоянно действующий мастер-класс учителей математики
МБОУ «Лицей №9 им. К.Э. Циолковского» г. Калуги
«Методические подходы к изучению тем, вызывающих наибольшие затруднения при обучении математике». Занятие №4.
Слайд 2Проблема: трудности при подготовке к ГИА:
нетипичность формулировок заданий в вариантах ГИА.
В учебниках используются стандартные формулировки, которые слабых обучающихся ставят в тупик, хотя после пояснений они легко с ними справляются;
различные вариации заданий, которые увеличивают число алгоритмов, которыми должны владеть учащиеся;
усвоение школьной программы;
учащиеся зачастую не «видят» чертеж, не замечают на нем уже известных теорем и закономерностей.;
в сложных задачах типа 16 (бывшая С4) в ЕГЭ , №26 в ОГЭ почти всегда надо применять при решении очень большое количество теорем и свойств, пользоваться одновременно всеми полученными знаниями и навыками, а зачастую и дополнительными фактами, которые есть не во всех учебниках или встречаются в виде задачи, что почти не встречается в алгебре, даже при решении сложных заданий.
В 2016-2017 в МБОУ «Лицей «9 им. К.Э. Циолковского» г. Калуги
ОГЭ
Задание №26 решили 2,81%;
Задание №25 решили 8,45%;
Задание №24 решили 39,43%,
ЕГЭ (профиль)
Задание №16 решили 1,54%.
Слайд 3Цель при подготовке к ГИА:
важно пройти всю программу целиком, а
не только «то, что пригодится на экзамене»,
повысить свою культуру вычислений,
развивать умение читать графики,
правильно использовать терминологию,
учить формулы.
Цель проведения мастер-класса:
Цель 1 (теоретического) этапа: осветить авторскую программу опыта подготовки к ВПР, ЕГЭ на уроках математики: «Применение производной и её свойств в задачах ГИА»;
Цель 2 (практического) этапа: показать формы и методы осуществления программы.
Слайд 4Задачи:
- продемонстрировать коллегам приемы работы с учащимися («работа с текстовой графической
информацией», «работа в группах над творческим заданием» и т.д.);
- прокомментировать эффективность применения приемов;
- отработать приемы в деятельностном режиме;
- представить основные результаты внедрения технологии проектирования;
- задействовать участников в процесс;
- сделать их активными, разбудить в них то, что скрыто даже для них самих; понять и устранить то, что ему мешает в саморазвитии, чтобы они проявили себя как творцы.
Слайд 5
Оборудование:
проектор, экран;
дидактический материал.
Основные этапы мастер - класса:
- организационный (приветствие,
введение в тему мастер-класса);
- демонстрационный (демонстрация наиболее эффективных приемов работы, комментарий, отработка приемов в деятельностном режиме);
- заключительный (подведение итогов, рефлексия).
Слайд 6Описание содержания, этапы МК
1.Решение задач по подготовке к ВПР, ЕГЭ по
математике по теме «Производная. Свойства производной в заданиях ЕГЭ» по определенным темам в 10 классе.
2.Решение задач по подготовке к ВПР, ЕГЭ по математике по теме «Производная. Свойства производной в заданиях ЕГЭ» по определенным темам при повторении пройденной учебной программы в 10, 11 классах.
Слайд 7Форма проведения занятия - интегрированное занятие
(лекционно-практическое).
Слайд 8
Интернет-ресурсы:
Для подготовки учащихся к первой части рекомендуем использовать ресурсы Открытого банка
http://opengia.ru/subjects/mathematics-9/topics/7.
https://reshimvse.com,
http://school.umk-spo.biz,
http://self-edu.ru,
https://www.uchportal.ru,
https://znanija.com,
http://matematikaege.ru и др. или сборникам тестов для подготовки к ЕГЭ, например, учебного пособия Математика 10-11 класс. Подготовка к ОГЭ, ЕГЭ, Д.А. Мальцев и др. М: Народное образование, 2013 и др.
Слайд 9Основные приемы работы, которые будут демонстрироваться слушателям:
1.прием «заготовки» Д/З на урок.
2.метод
проектов.
3.метод применения ИКТ.
4.прием опережающего обучения.
5.методический приём «комментируемое управление».
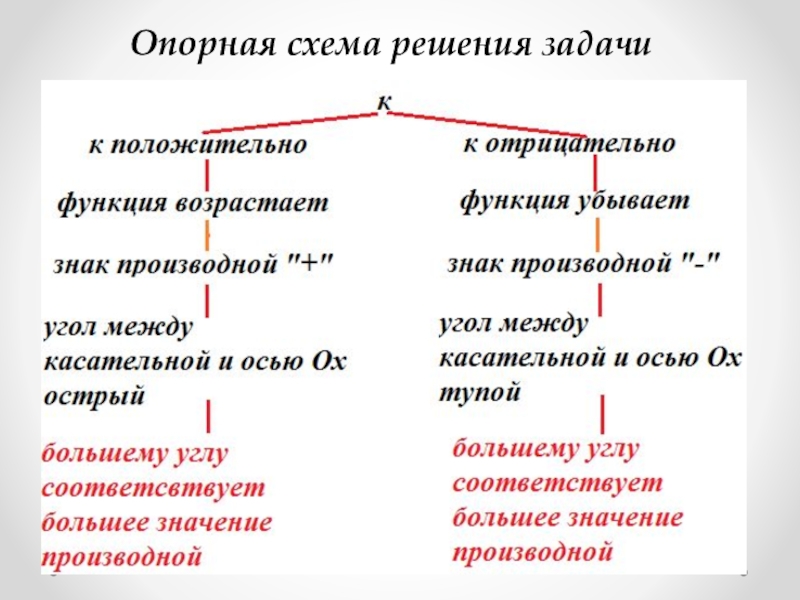
6.опорные схемы.
5.прием «Д/З по задачам ЕГЭ с дальнейшей презентацией решений».
6.метод создания заданий творческого характера.
7.приём презентации полученных результатов на уроке путем сканирования материала, решения.
8.приёмы обработки графической и текстовой информации.
9. приём «Тонкие» и «Толстые» вопросы.
10.приём «Составление краткой записи задачи».
11. приём «Вопросы к тексту».
12.приём «Верные и неверные утверждения».
13.приём Задания «на дополнение информации».
Слайд 1014.приём Задания «на восстановление текста».
15.приём Задания «на соотнесение».
16. приём взаимопроверки и
взаимообучения.
17. методика «Взаимообмен заданиями».
18.технология групповой работы.
19. технология развития критического мышления.
20.приём «кластер» .
21.метод мозгового штурма.
22.приём «Корзина» идей, понятий, имен…
23.приём «Фантастическая добавка».
24.прием рефлексии «Комплимент».
25.прием рефлексии Техника «Рефлексивная мишень».
26.прием рефлексии «А напоследок я скажу».
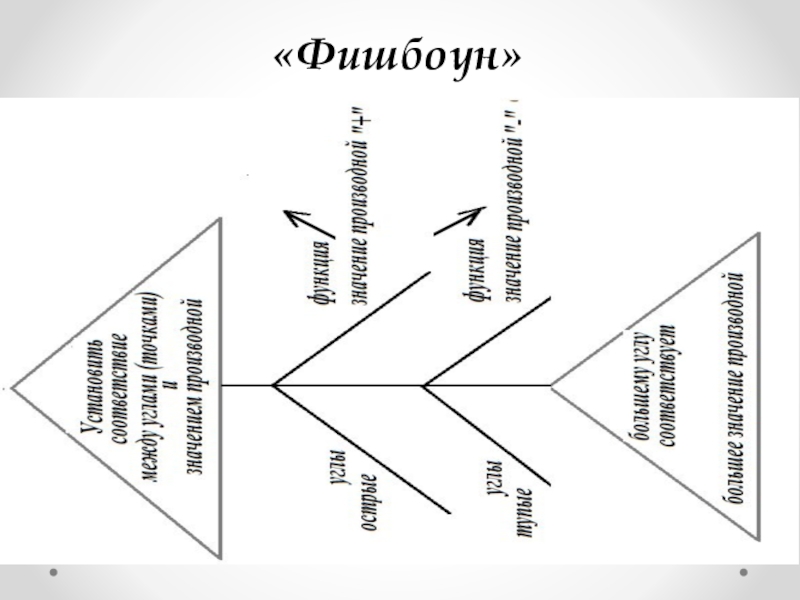
27. приём «Фишбоун».
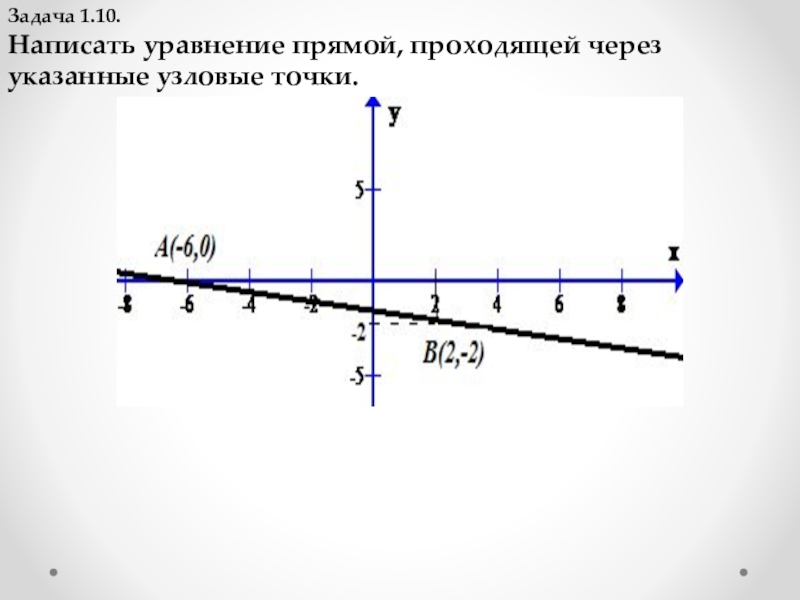
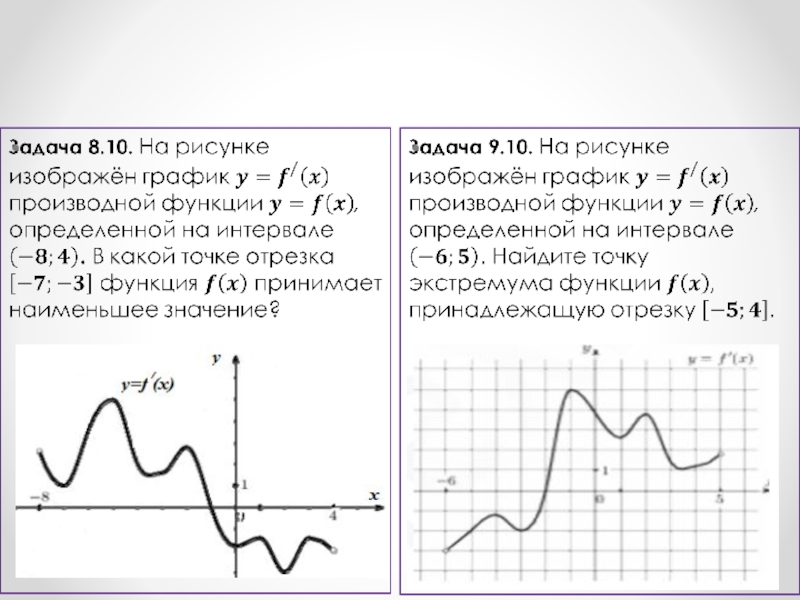
Слайд 13Задача 1.10.
Написать уравнение прямой, проходящей через указанные узловые точки.
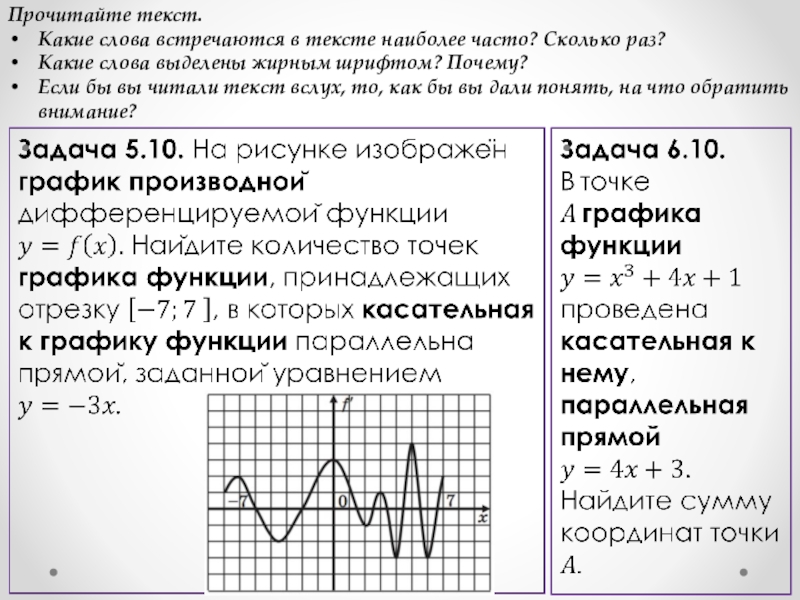
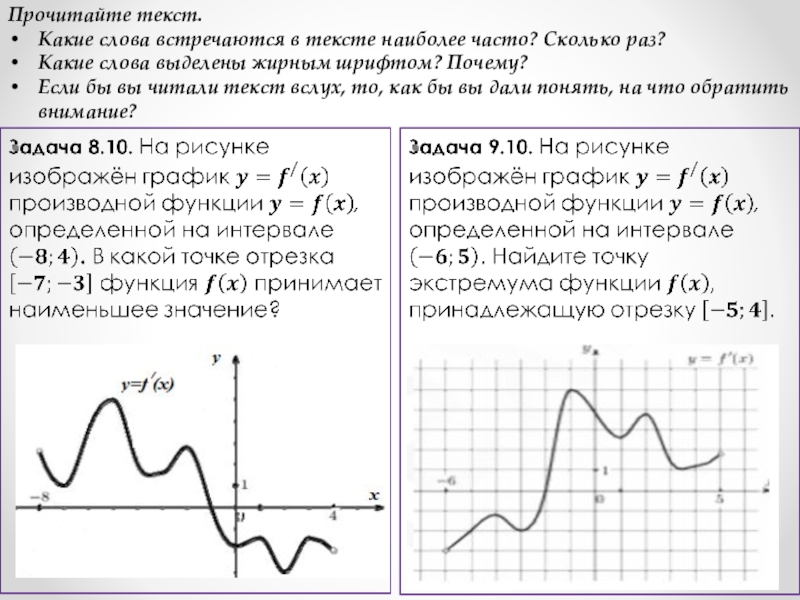
Слайд 16Прочитайте текст.
Какие слова встречаются в тексте наиболее часто? Сколько раз?
Какие слова
выделены жирным шрифтом? Почему?
Если бы вы читали текст вслух, то, как бы вы дали понять, на что обратить внимание?
С 2017/2018 учебного года МБОУ «Лицей №9 им. К.Э. Циолковского» г. Калуги присвоен статус региональной инновационной площадки «Формирование у обучающихся единого культурного кода России на основе продвижения передовых методик и практик в рамках реализации Концепции филологического образования».
Слайд 17
Прочитайте текст.
Какие слова встречаются в тексте наиболее часто? Сколько раз?
Какие слова
выделены жирным шрифтом? Почему?
Если бы вы читали текст вслух, то, как бы вы дали понять, на что обратить внимание?
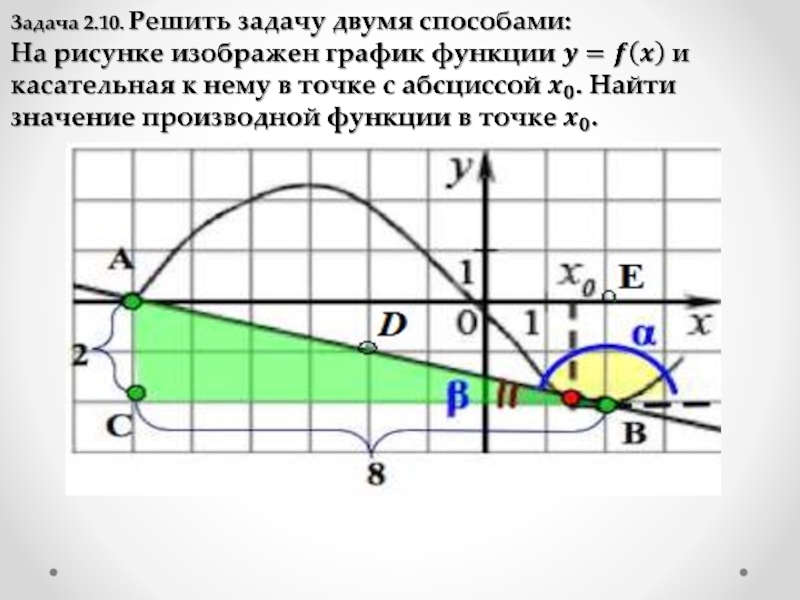
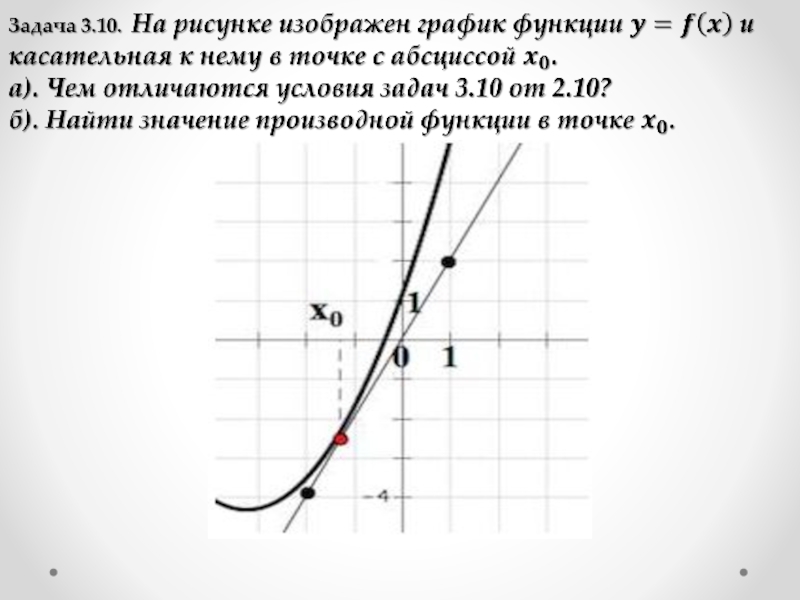
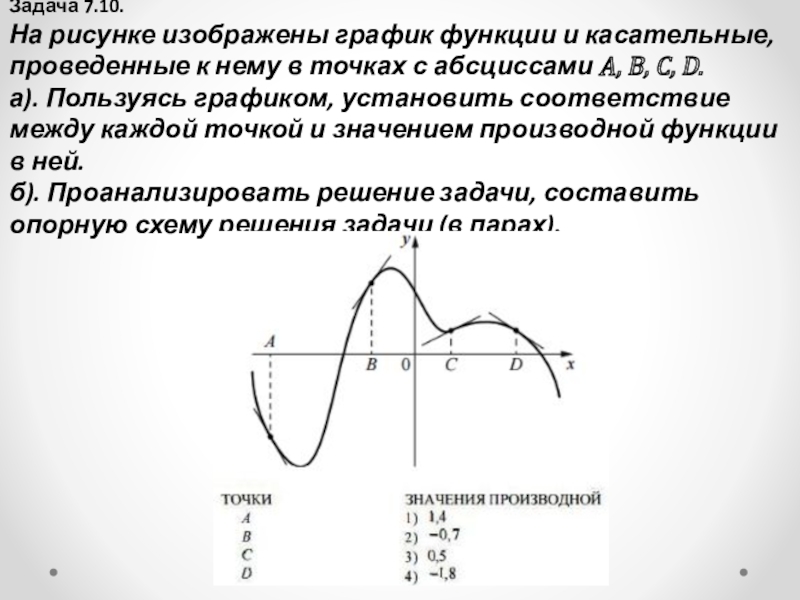
Слайд 18Задача 7.10.
На рисунке изображены график функции и касательные, проведенные к нему
в точках с абсциссами A, B, C, D.
а). Пользуясь графиком, установить соответствие между каждой точкой и значением производной функции в ней.
б). Проанализировать решение задачи, составить опорную схему решения задачи (в парах).
Слайд 21
Прочитайте текст.
Какие слова встречаются в тексте наиболее часто? Сколько раз?
Какие слова
выделены жирным шрифтом? Почему?
Если бы вы читали текст вслух, то, как бы вы дали понять, на что обратить внимание?
Слайд 23
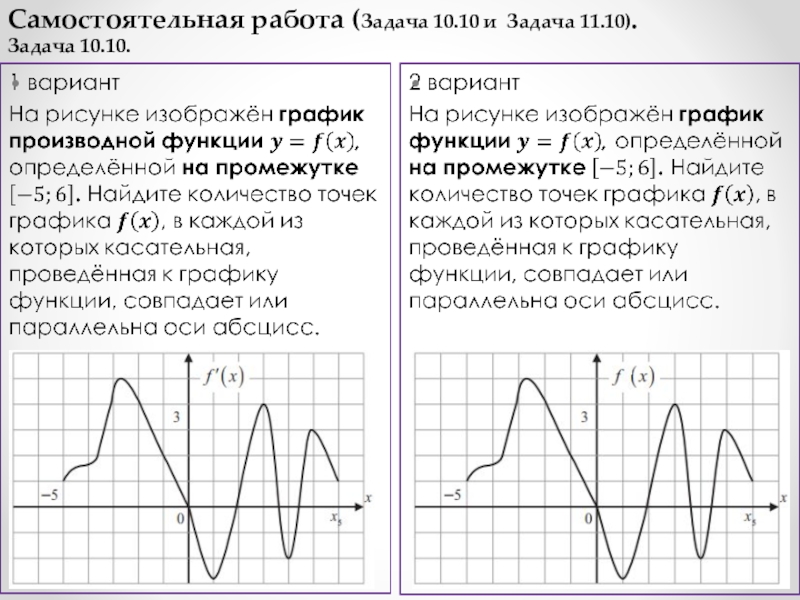
Самостоятельная работа (Задача 10.10 и Задача 11.10).
Задача 10.10.
Слайд 24
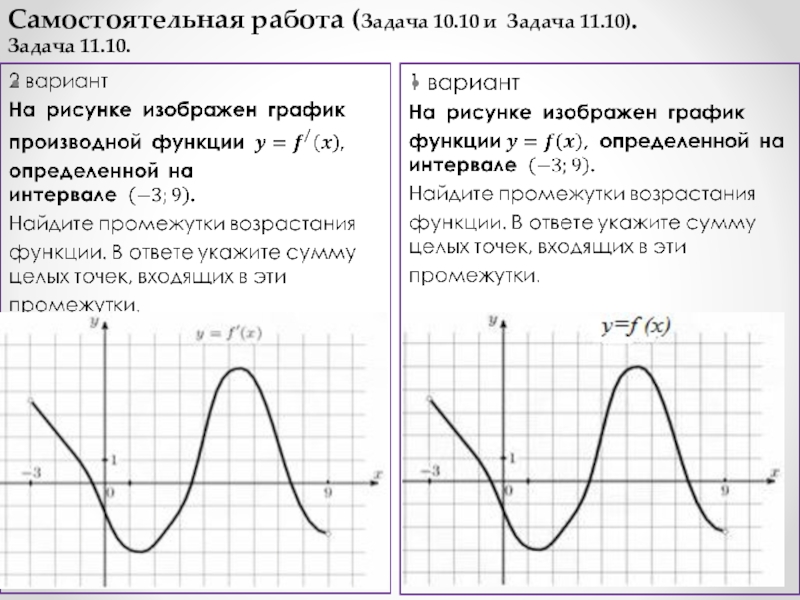
Самостоятельная работа (Задача 10.10 и Задача 11.10).
Задача 11.10.
Слайд 25От простого к сложному на уроках повторения
в 11 классе.
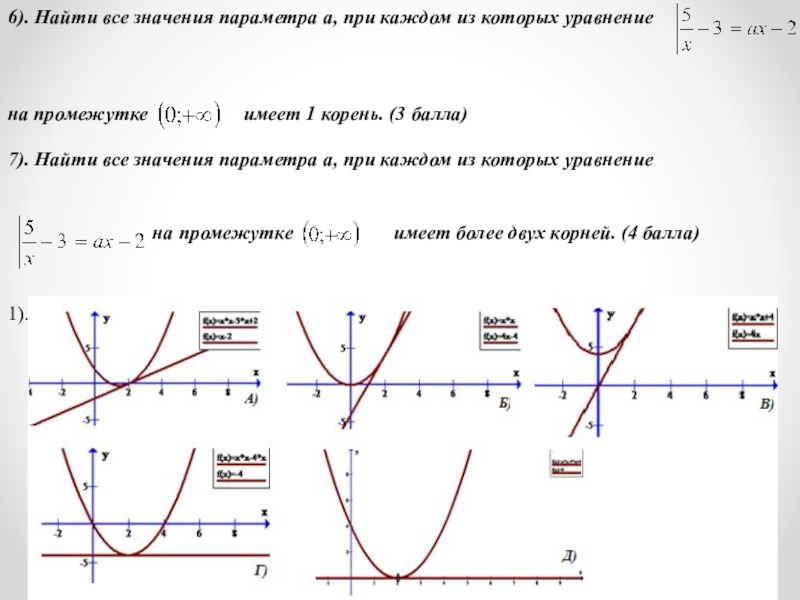
Слайд 266). Найти все значения параметра а, при каждом из которых уравнение
на промежутке имеет 1 корень. (3 балла)
7). Найти все значения параметра а, при каждом из которых уравнение
на промежутке имеет более двух корней. (4 балла)
1).
Слайд 30Задача 4.11. (Еженедельная учебно-методическая газета «Математика», издательский дом «Первое сентября», №16,
2004). При каких значениях параметра а уравнение
имеет единственное решение.
Слайд 311 способ. Аналитический способ. Рассмотрим два случая:
1.
При этом значении параметра а уравнение принимает вид
Это единственное решение.
2. Тогда - квадратное уравнение, дискриминант которого
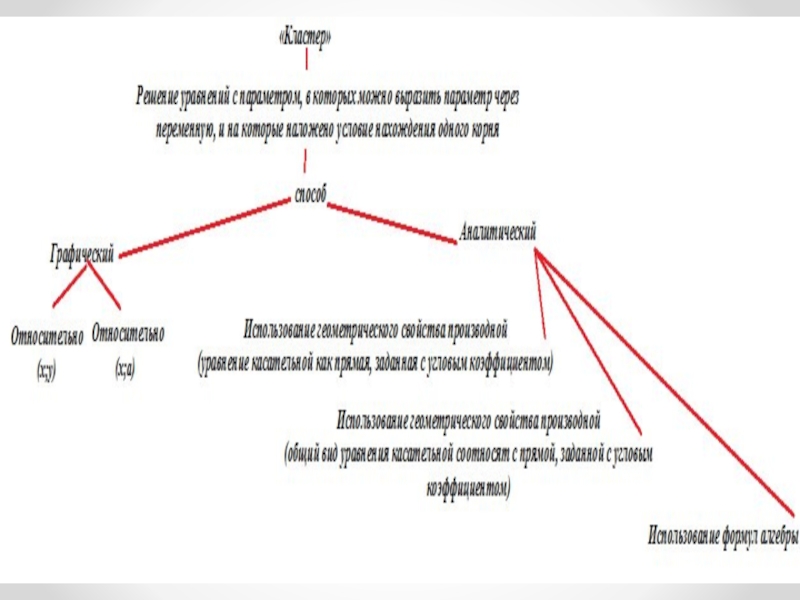
Слайд 32Способы(методы) решения задач с параметром:
Способ I (аналитический). Это способ так
называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра.
Комментарий. Аналитический способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им.
Способ II (графический). В зависимости от задачи (с переменной х и параметром а) рассматриваются графики или в координатной плоскости (х; у), или в координатной плоскости (х; а).
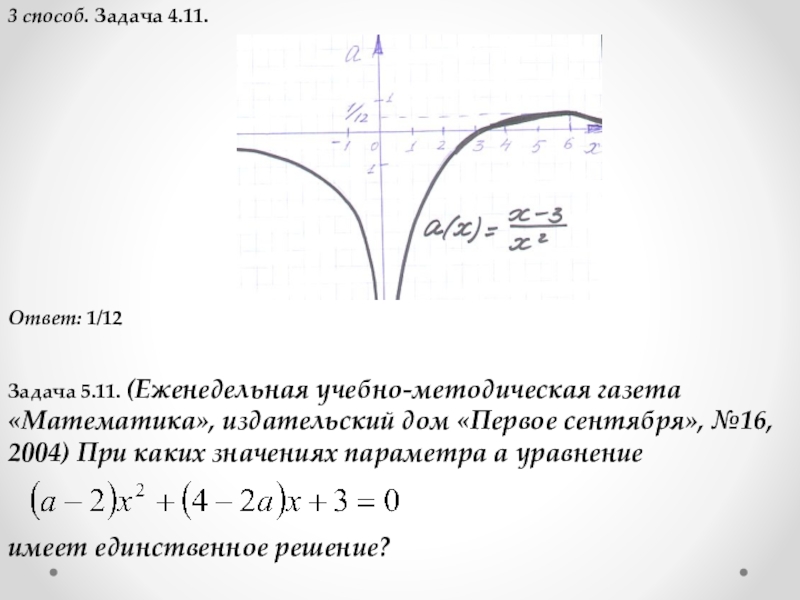
Слайд 333 способ. Задача 4.11.
Ответ: 1/12
Задача 5.11. (Еженедельная учебно-методическая газета «Математика»,
издательский дом «Первое сентября», №16, 2004) При каких значениях параметра а уравнение
имеет единственное решение?
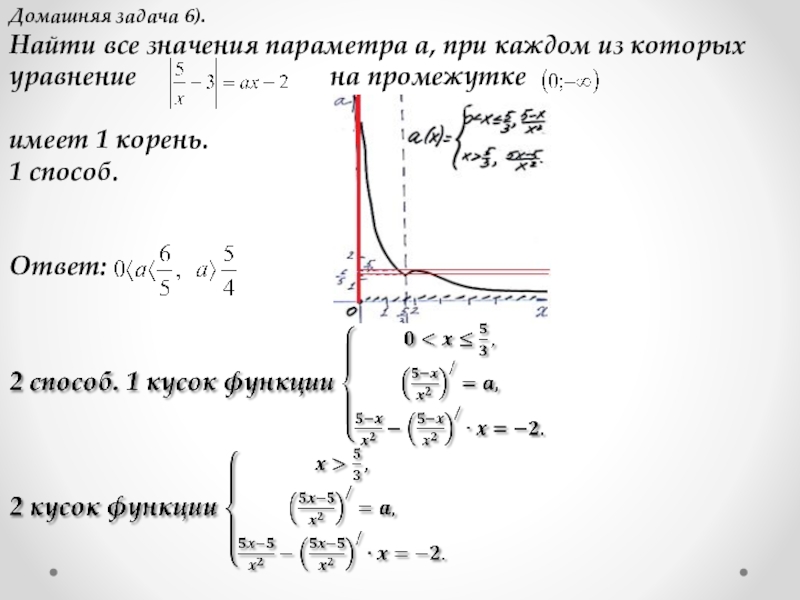
Слайд 36Домашняя задача 6).
Найти все значения параметра а, при каждом из которых
уравнение на промежутке
имеет 1 корень.
Слайд 37Домашняя задача 6).
Найти все значения параметра а, при каждом из которых
уравнение на промежутке
имеет 1 корень.
1 способ.
Ответ:
Слайд 38
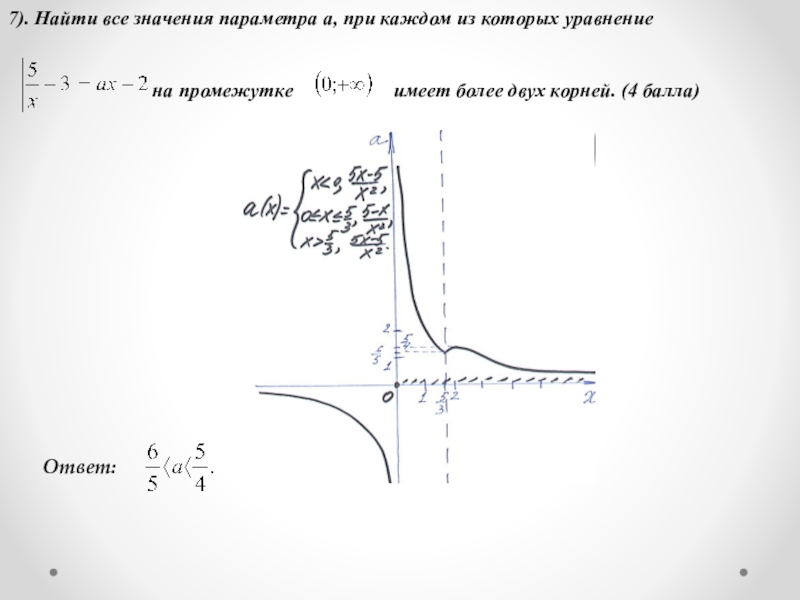
7). Найти все значения параметра а, при каждом из которых
уравнение
на промежутке имеет более двух корней. (4 балла)
Ответ:
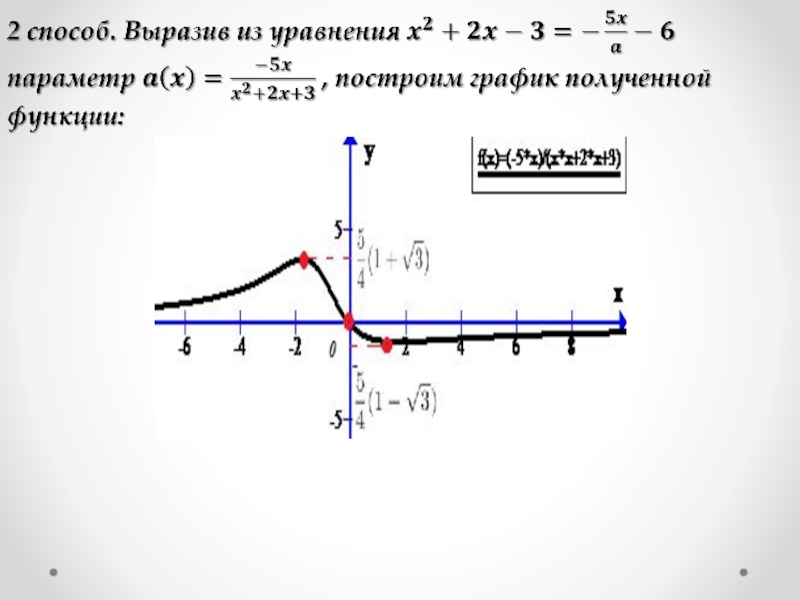
Слайд 40Решение.
1 способ. Графиком f(x ) является парабола, пересекающая ось Ox
в точках x=-3 и x=1, а ось Oy в точке y=-3.
Графиком при каждом фиксированном a является прямая:
1). При a=0 это прямая x=0. Она имеет ровно одну точку пересечения с f(x), а именно, точку (0;-3).
2). При a≠0 это пучок прямых ,
проходящих через точку 0;-6.
Графики будут иметь ровно 1 точку пересечения при тех значениях a, при которых прямая y будет касаться параболы. Условия касания:
Ответ:
Слайд 42Прием рефлексии «Комплимент»,
прием рефлексии «А напоследок я скажу»,
прием рефлексии
Техника «Рефлексивная мишень».