- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презентація з геометрії для 8 класу Вписані чотирикутники
Содержание
- 1. Презентація з геометрії для 8 класу Вписані чотирикутники
- 2. ОзначенняЯкщо всі вершини чотирикутника лежать на колі,
- 3. Не будь-який чотирикутник можна вписати в коло
- 4. Яку ж властивість повинен мати чотирикутник,
- 5. Сума протилежних кутів чотирикутника, вписаного в коло
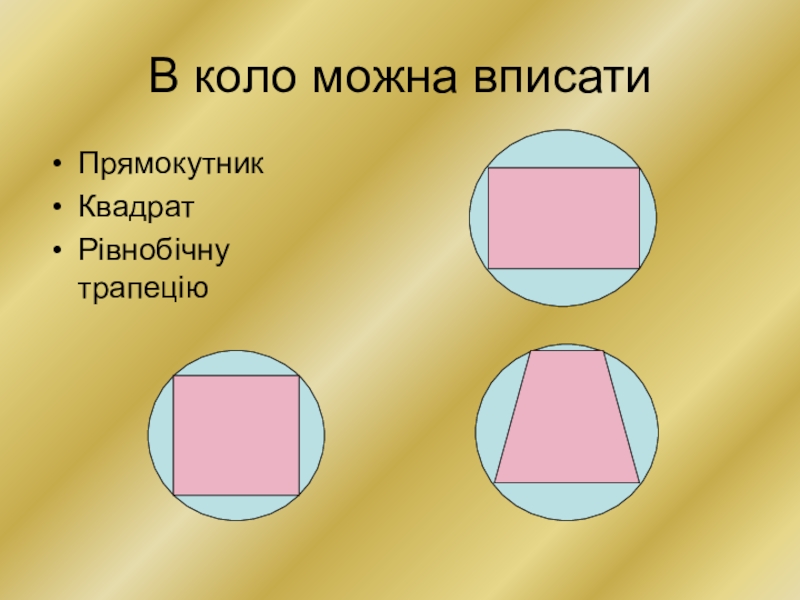
- 6. В коло можна вписатиПрямокутникКвадратРівнобічну трапецію
- 7. Центр кола,описаного навколо чотирикутника, рівновіддалений від його
- 8. Задача прикладного змістуМенша сторона футбольного поля, що
- 9. Задачі на застосування властивості чотирикутника, вписаного
- 10. Джерела інформаціїГеометрія: Підручник для 8 класу з
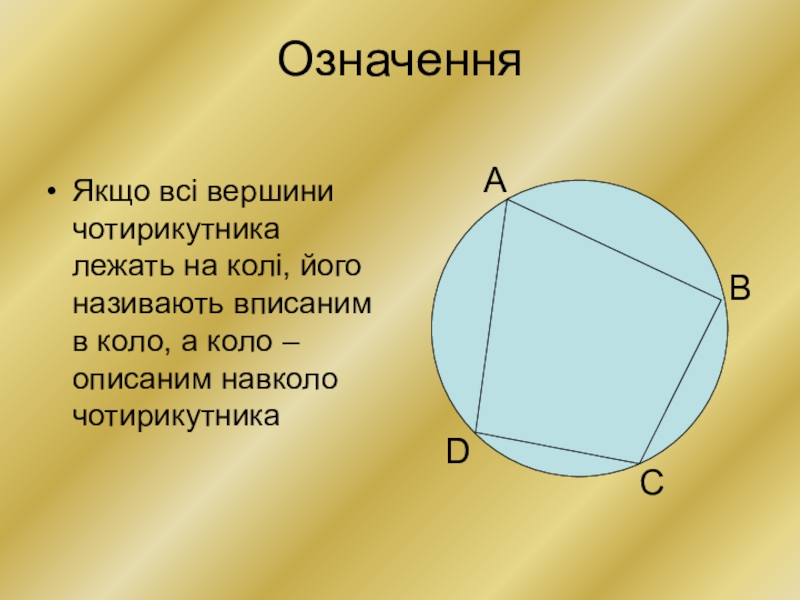
ОзначенняЯкщо всі вершини чотирикутника лежать на колі, його називають вписаним в коло, а коло –описаним навколо чотирикутникаАВСD
Слайд 2Означення
Якщо всі вершини чотирикутника лежать на колі, його називають вписаним в
коло, а коло –описаним навколо чотирикутника
А
В
С
D
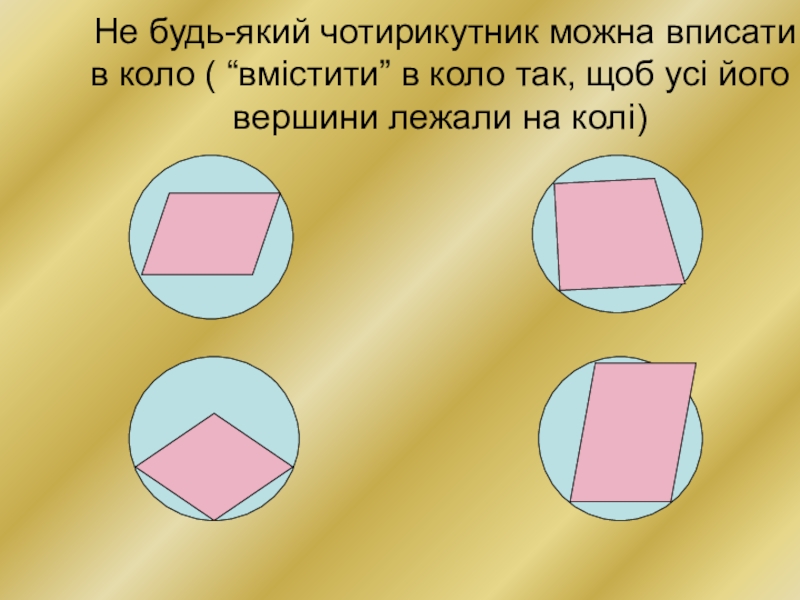
Слайд 3Не будь-який чотирикутник можна вписати в коло ( “вмістити” в коло
так, щоб усі його вершини лежали на колі)
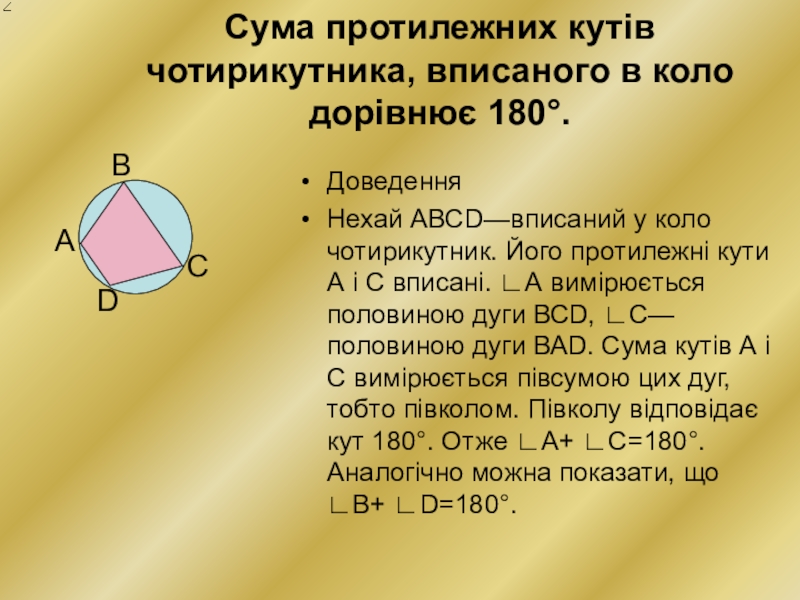
Слайд 5Сума протилежних кутів чотирикутника, вписаного в коло дорівнює 180°.
Доведення
Нехай АВСD—вписаний у
коло чотирикутник. Його протилежні кути А і С вписані. ∟А вимірюється половиною дуги ВСD, ∟С—половиною дуги ВАD. Сума кутів А і С вимірюється півсумою цих дуг, тобто півколом. Півколу відповідає кут 180°. Отже ∟А+ ∟С=180°. Аналогічно можна показати, що ∟В+ ∟D=180°.
А
В
С
D
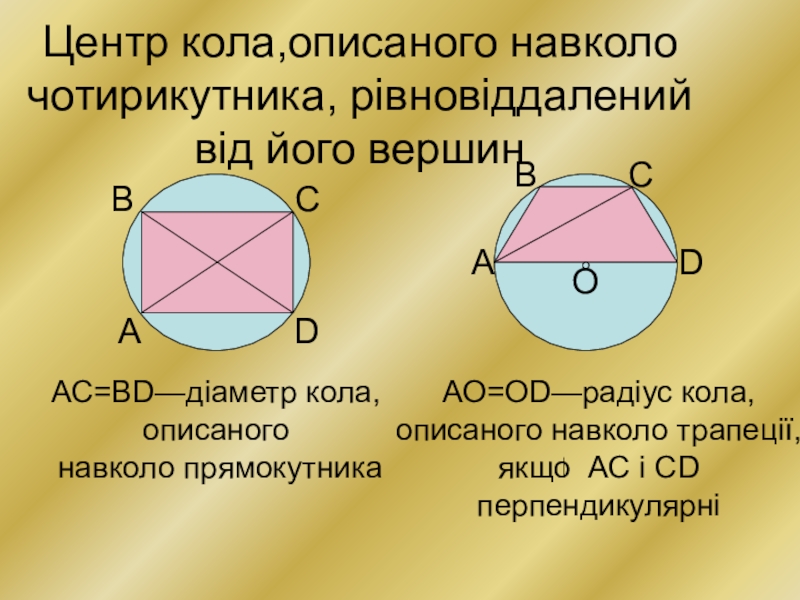
Слайд 7Центр кола,описаного навколо чотирикутника, рівновіддалений від його вершин
А
В
С
D
АС=ВD—діаметр кола,
описаного
навколо прямокутника
А
В
С
D
АО=ОD—радіус
кола,
описаного навколо трапеції,
якщо АС і СD
перпендикулярні
описаного навколо трапеції,
якщо АС і СD
перпендикулярні
О
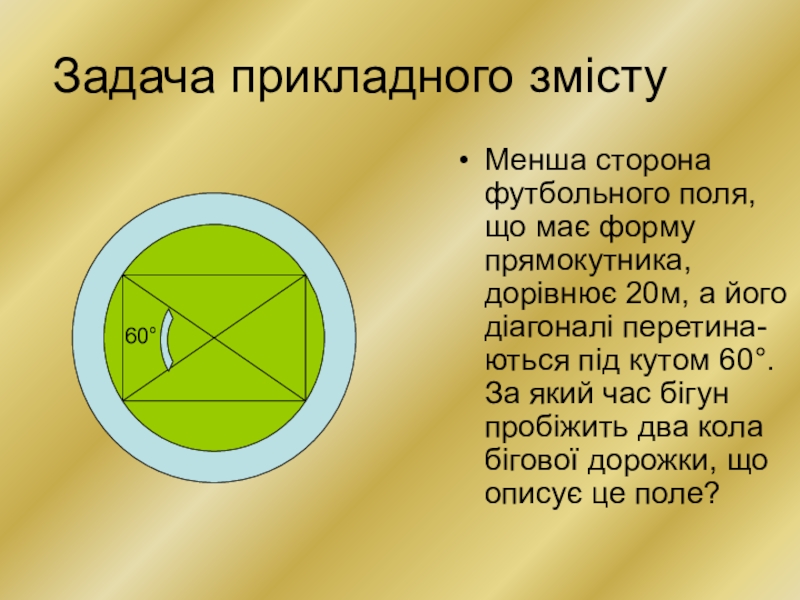
Слайд 8Задача прикладного змісту
Менша сторона футбольного поля, що має форму прямокутника, дорівнює
20м, а його діагоналі перетина-ються під кутом 60°. За який час бігун пробіжить два кола бігової дорожки, що описує це поле?
60°
Слайд 9Задачі на застосування
властивості чотирикутника, вписаного в коло
Два послідовні кути вписаного
чотирикутника дорівнюють 80° і 120°. Знайдіть два інші його кути.
Чи можна описати коло навколо чотирикутника, кути якого, взяті послідовно,пропорційні числам: а) 2,5,7,4; б) 3,4,7,5?
Менша сторона прямокутника дорівнює 12см,а кут між діагоналями дорівнює 60°. Знайдіть радіус кола, описаного навколо прямокутника.
Діагональ трапеції перпендикулярна до бічної сторони, що дорівнює 6см. Знайдіть радіус кола, описаного навколо трапеції, якщо її гострий кут дорівнює 60°.
Кути трапеції пропорційні числам 1 і 2,а діагональ є бісектрисою гострого кута. Знайдіть радіус описаного кола, якщо бічна сторона трапеції дорівнює 12см.
Чи можна описати коло навколо чотирикутника, кути якого, взяті послідовно,пропорційні числам: а) 2,5,7,4; б) 3,4,7,5?
Менша сторона прямокутника дорівнює 12см,а кут між діагоналями дорівнює 60°. Знайдіть радіус кола, описаного навколо прямокутника.
Діагональ трапеції перпендикулярна до бічної сторони, що дорівнює 6см. Знайдіть радіус кола, описаного навколо трапеції, якщо її гострий кут дорівнює 60°.
Кути трапеції пропорційні числам 1 і 2,а діагональ є бісектрисою гострого кута. Знайдіть радіус описаного кола, якщо бічна сторона трапеції дорівнює 12см.
Слайд 10Джерела інформації
Геометрія: Підручник для 8 класу з поглибленим вивченням математики./
А.Г.Мерзляк та ін.-Харків, Гімназія,2009
Геометрия: Учебник для 7-9 кл. сред. шк./ Л. С. Атанасян и др.- М.: Просвещение, 1992
www. erudition. ru
www. college. ru
http: //school-collection
Геометрия: Учебник для 7-9 кл. сред. шк./ Л. С. Атанасян и др.- М.: Просвещение, 1992
www. erudition. ru
www. college. ru
http: //school-collection