- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Окружность, геометрия, 8 класс
Содержание
- 1. Презентация.Окружность, геометрия, 8 класс
- 2. Окружность — геометрическое место всех точек плоскости , равноудалённых
- 3. ОABЦентр окружности -точка, от которой равноудалены на
- 4. Прямая может не иметь с окружностью общих
- 5. Если прямая проходит через центр окружности, то
- 6. d
- 7. 2) d = гВ этом случае ОН=
- 8. d > гВ этом случае ОН > г,
- 9. Прямая и окружность могут иметь одну или
- 10. ДоказательствоПусть р — касательная к окружности с
- 11. Касательная к окружностиРассмотрим две касательные к окружности
- 12. Доказательство:По теореме о свойстве касательной углы 1
- 13. ДоказательствоИз условия теоремы следует, что данный радиус
- 14. На этой теореме основано решение задач на
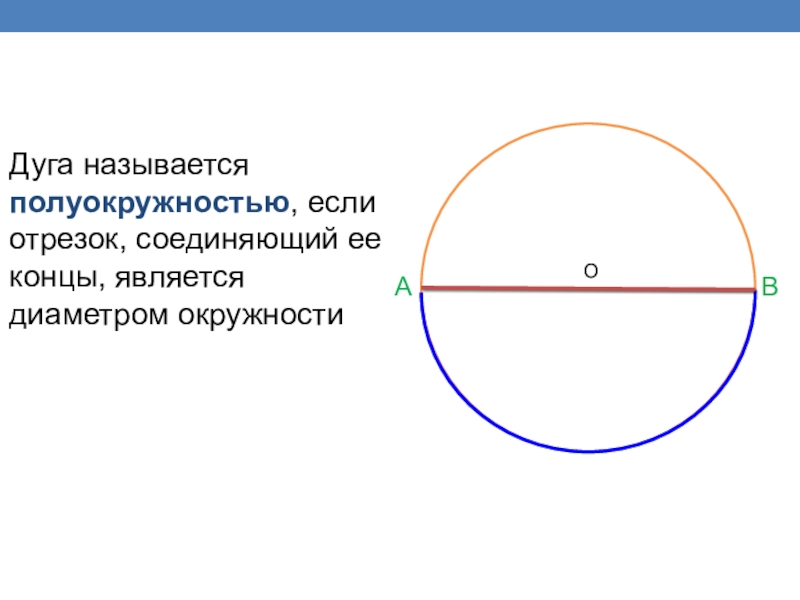
- 15. Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружностиABO
- 16. Угол с вершиной в центре окружности называется
- 17. ABOОABОABLLДугу окружности можно измерять в градусах. Если
- 18. Теорема о вписанном углеВписанный угол измеряется половиной дуги, на которую он опираетсяОABMC
- 19. Теорема о вписанном углеПусть < ABC —
- 20. Три возможных случая расположения луча ВО относительно
- 21. Следствие 1Следствие 2Вписанные углы, опирающиеся на одну
- 22. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хордыBАСDE1234Теорема
- 23. Пусть хорды АВ и CD пересекаются в
- 24. Орнаменты
- 25. http://ru.wikipedia.org/wiki/%CE%EA%F0%F3%E6%ED%EE%F1%F2%FChttp://www.problems.ru/thes.php?letter=14http://uztest.ru/abstracts/?idabstract=149650http://slovo.ws/urok/geometr/07/003/164.htmlhttp://www.liveinternet.ru/users/galinaak/post199693536/
- 26. Слайд 26
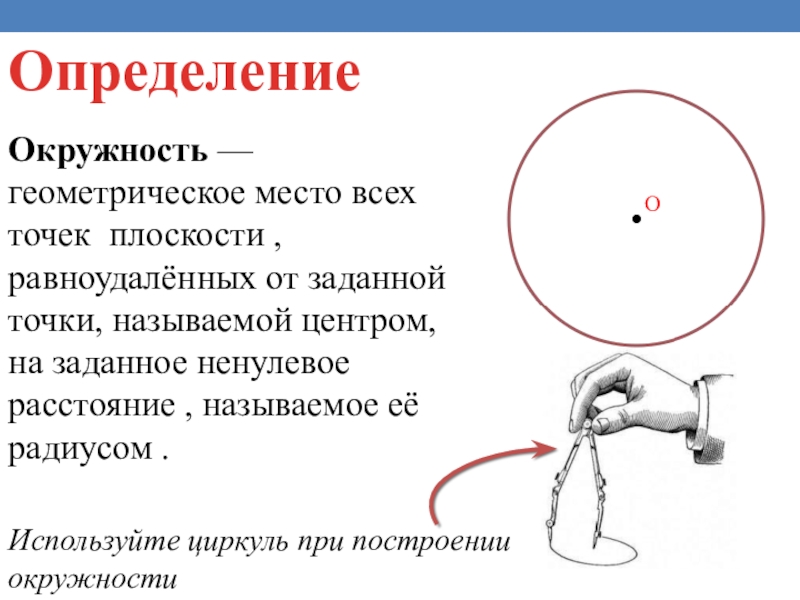
Слайд 2Окружность — геометрическое место всех точек плоскости , равноудалённых от заданной точки, называемой
О
Определение
Используйте циркуль при построении окружности
Слайд 3О
A
B
Центр окружности -точка, от которой равноудалены на заданное расстояние все точки
Отрезок, соединяющий любую точку окружности с ее центром, а также его длина, называется радиусом окружности.
ОA- радиус окружности
Диаметром окружности называется хорда данной окружности, проходящая через ее центр.
Отрезок, соединяющий две точки окружности, называется хордой окружности, а также хордой ограниченного ей круга.
AB- хорда, проходящая через ее центр О
ВСПОМНИ!!!
Слайд 4
Прямая может не иметь с окружностью общих точек; иметь с окружностью
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Точка касания двух окружностей лежит на линии, соединяющей их центры.
Свойства окружности
Слайд 5Если прямая проходит через центр окружности, то она пересекает окружность в
Пусть прямая р не проходит через центр о окружности радиуса г.
Проведем перпендикуляр ОН к прямой р и обозначим буквой d длину этого перпендикуляра, т. е. расстояние от центра данной окружности до прямой
О
H
p
Взаимное расположение прямой
и окружности
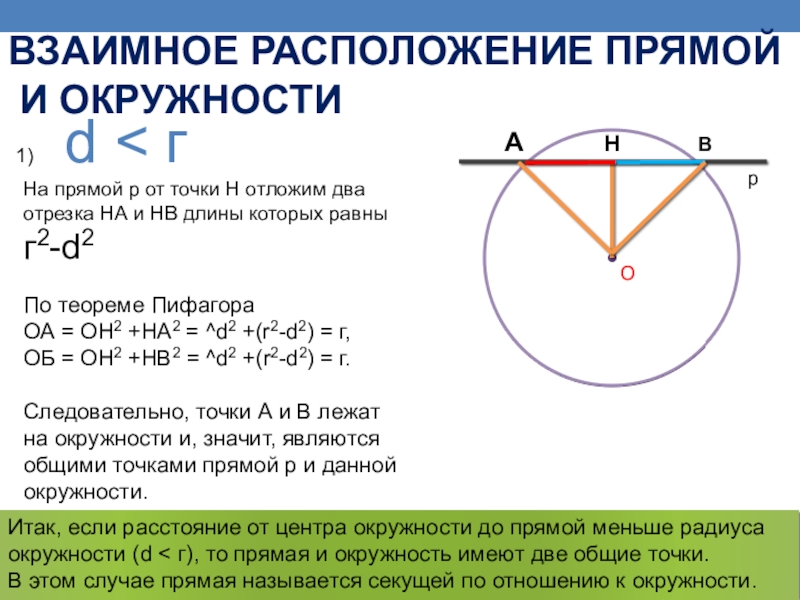
Слайд 6 d
По теореме Пифагора
ОА = ОН2 +НА2 = ^d2 +(r2-d2) = г,
ОБ = OH2 +НВ2 = ^d2 +(r2-d2) = г.
Следовательно, точки А и В лежат на окружности и, значит, являются общими точками прямой р и данной окружности.
Взаимное расположение прямой
и окружности
О
А
B
H
p
Итак, если расстояние от центра окружности до прямой меньше радиуса окружности (d < г), то прямая и окружность имеют две общие точки.
В этом случае прямая называется секущей по отношению к окружности.
Слайд 72) d = г
В этом случае ОН= г, т. е. точка
Прямая р и окружность не имеют других общих точек, так как для любой точки М прямой р, отличной от точки Н, ОМ > ОН = г (наклонная ОМ больше перпендикуляра ОН), и, следовательно, точка М не лежит на окружности.
О
M
H
p
Итак, если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
Взаимное расположение прямой
и окружности
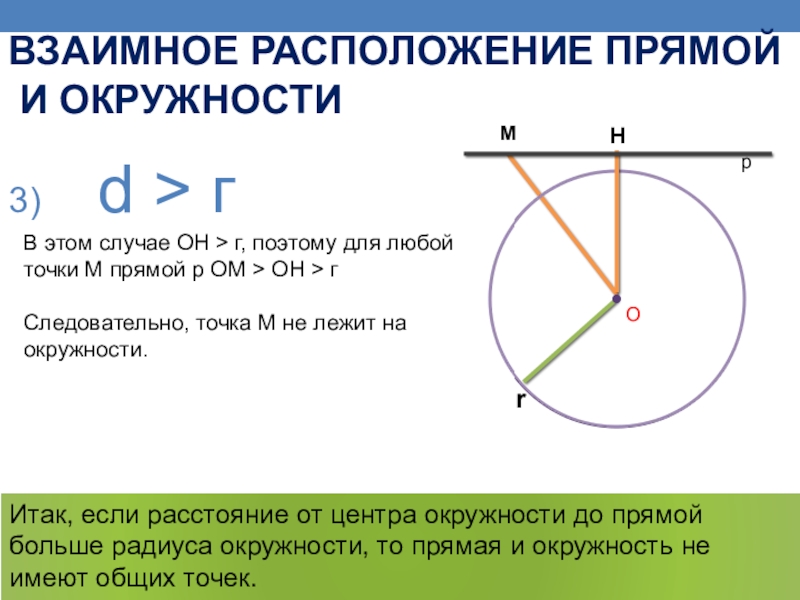
Слайд 8 d > г
В этом случае ОН > г, поэтому для любой точки
Следовательно, точка М не лежит на окружности.
О
M
H
p
r
Итак, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
Взаимное расположение прямой
и окружности
Слайд 9Прямая и окружность могут иметь одну или две общие точки и
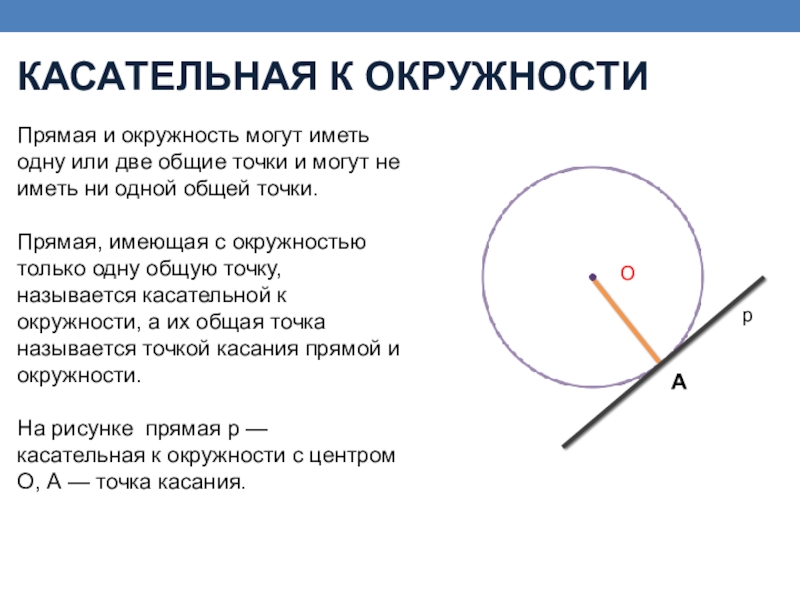
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
На рисунке прямая р — касательная к окружности с центром О, А — точка касания.
Касательная к окружности
О
A
p
Слайд 10
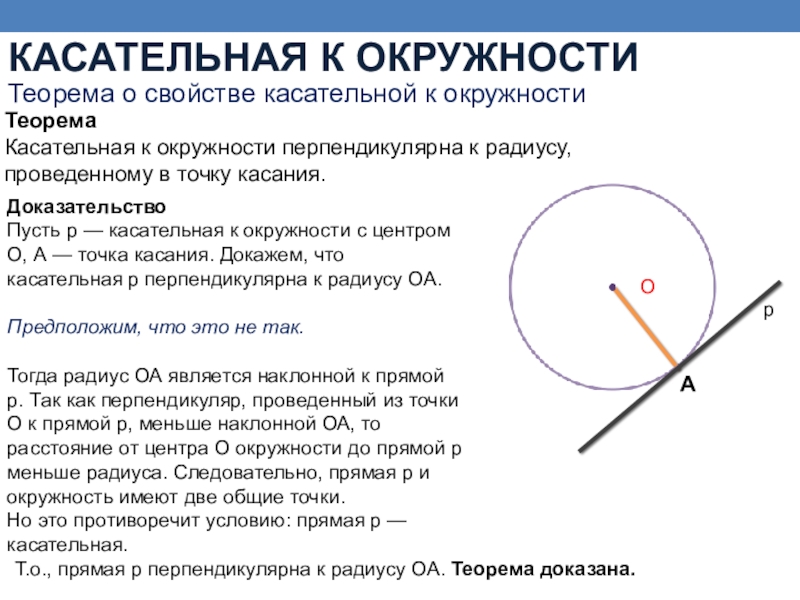
Доказательство
Пусть р — касательная к окружности с центром О, А —
Предположим, что это не так.
Тогда радиус ОА является наклонной к прямой р. Так как перпендикуляр, проведенный из точки О к прямой р, меньше наклонной ОА, то расстояние от центра О окружности до прямой р меньше радиуса. Следовательно, прямая р и окружность имеют две общие точки.
Но это противоречит условию: прямая р — касательная.
Касательная к окружности
О
A
p
Теоремa о свойстве касательной к окружности
Теорема
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Т.o., прямая р перпендикулярна к радиусу ОА. Теорема доказана.
Слайд 11Касательная к окружности
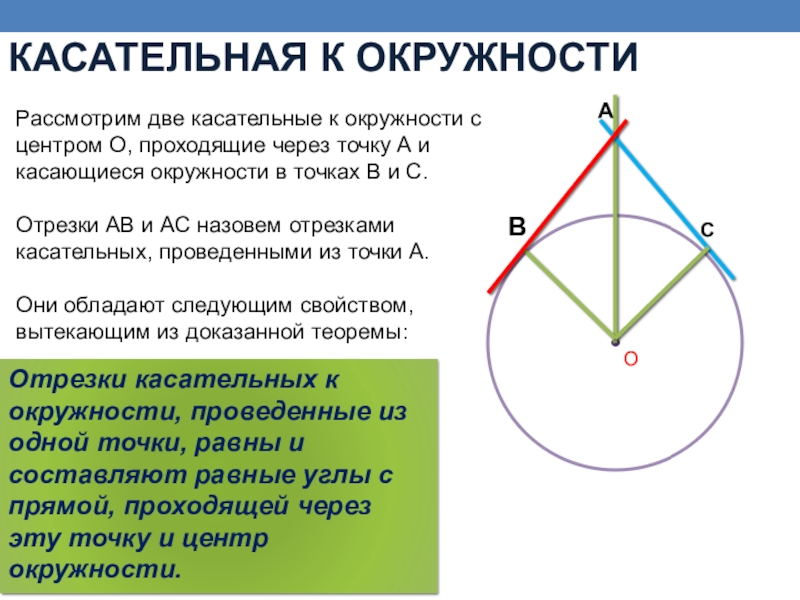
Рассмотрим две касательные к окружности с центром О, проходящие
Отрезки АВ и АС назовем отрезками касательных, проведенными из точки А.
Они обладают следующим свойством, вытекающим из доказанной теоремы:
О
B
C
A
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
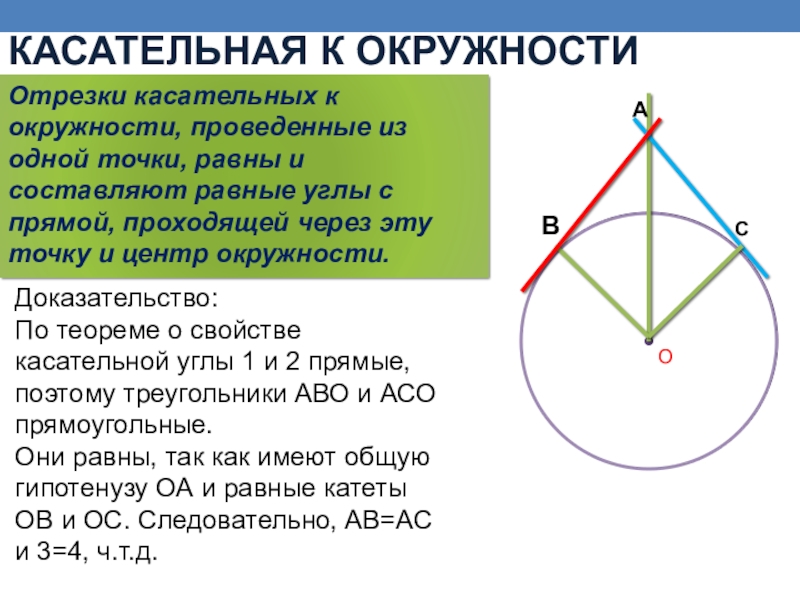
Слайд 12Доказательство:
По теореме о свойстве касательной углы 1 и 2 прямые, поэтому
Они равны, так как имеют общую гипотенузу ОА и равные катеты ОВ и ОС. Следовательно, АВ=АС и 3=4, ч.т.д.
О
B
C
A
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Касательная к окружности
Слайд 13Доказательство
Из условия теоремы следует, что данный радиус является перпендикуляром, проведенным из
Теорема, обратная теореме о свойстве касательной (признак касательной)
Теорема
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Слайд 14На этой теореме основано решение задач на построение касательной. Решим одну
Теорема, обратная теореме о свойстве касательной (признак касательной)
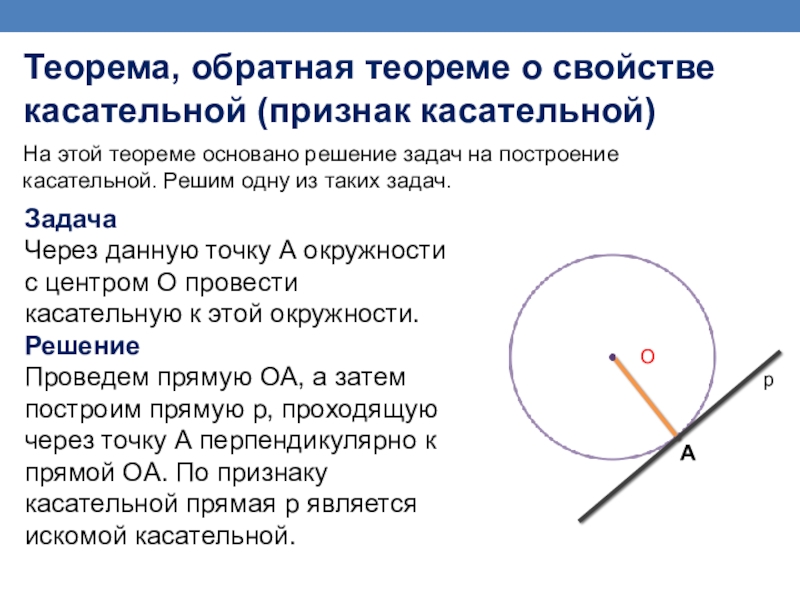
Задача
Через данную точку А окружности с центром О провести касательную к этой окружности.
Решение
Проведем прямую ОА, а затем построим прямую р, проходящую через точку А перпендикулярно к прямой ОА. По признаку касательной прямая р является искомой касательной.
О
A
p
Слайд 15Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности
A
B
O
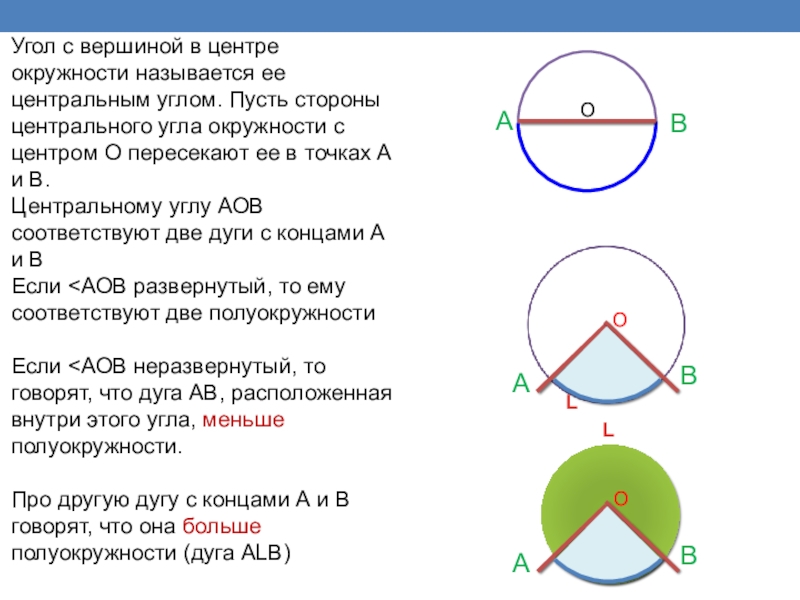
Слайд 16Угол с вершиной в центре окружности называется ее центральным углом. Пусть
Центральному углу АОВ соответствуют две дуги с концами А и В
Если <АОВ развернутый, то ему соответствуют две полуокружности
Если <АОВ неразвернутый, то говорят, что дуга АВ, расположенная внутри этого угла, меньше полуокружности.
Про другую дугу с концами А и В говорят, что она больше полуокружности (дуга ALB)
A
B
O
О
A
B
О
A
B
L
L
Слайд 17A
B
O
О
A
B
О
A
B
L
L
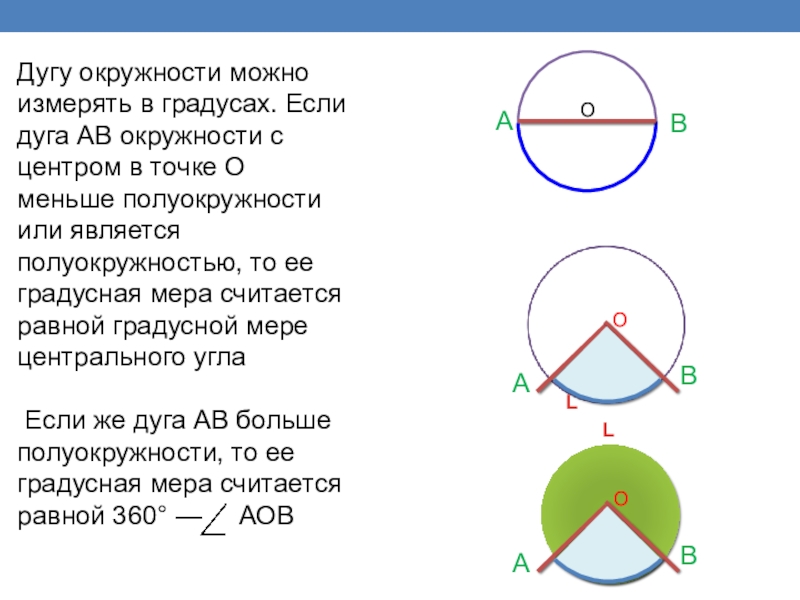
Дугу окружности можно измерять в градусах. Если дуга АВ окружности с
Если же дуга АВ больше полуокружности, то ее градусная мера считается равной 360° — АОВ
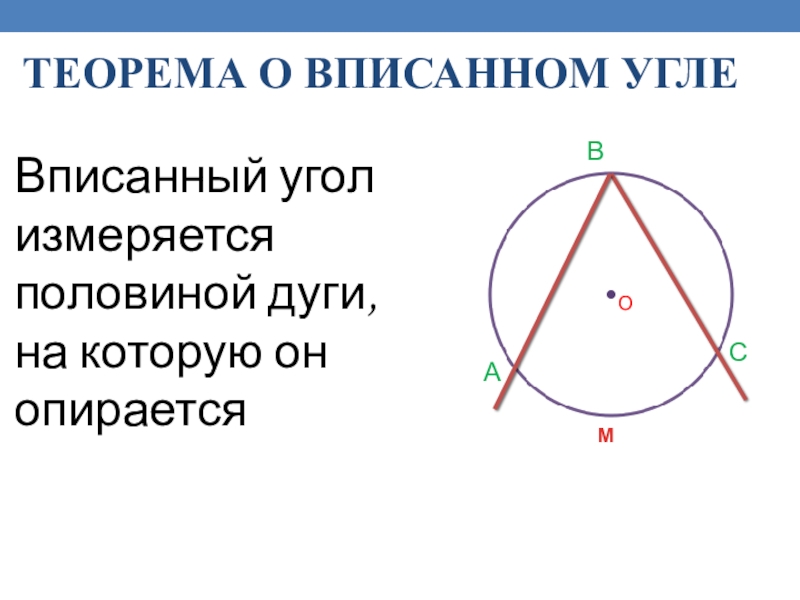
Слайд 18Теорема о вписанном угле
Вписанный угол измеряется половиной дуги, на которую он
О
A
B
M
C
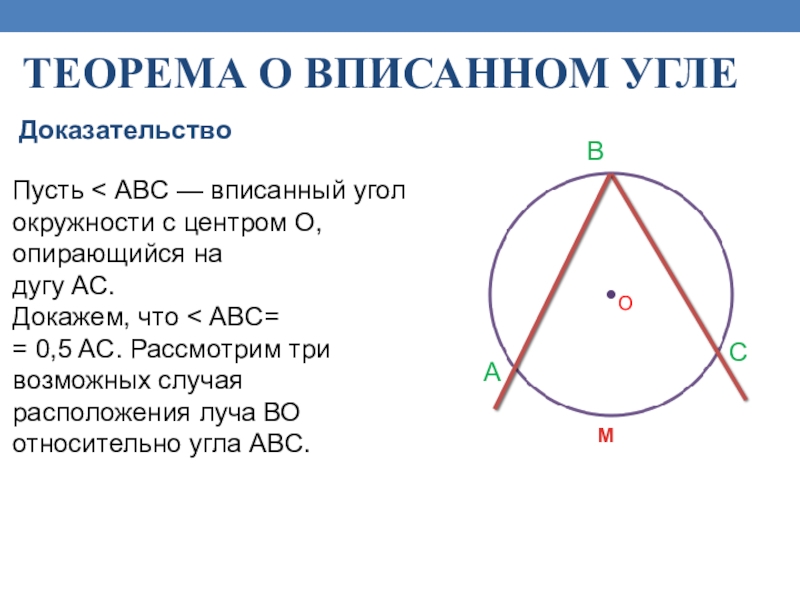
Слайд 19Теорема о вписанном угле
Пусть < ABC — вписанный угол окружности с
дугу АС.
Докажем, что < ABC=
= 0,5 AC. Рассмотрим три возможных случая расположения луча ВО относительно угла ABC.
О
A
B
M
C
Доказательство
Слайд 20Три возможных случая расположения луча ВО относительно угла АВС
Луч ВО совпадает
Луч ВО делит угол АВС на два угла (Рис. б)
Луч ВО не делит угол АВС на два угла и не совпадает со стороной этого угла (Рис. в)
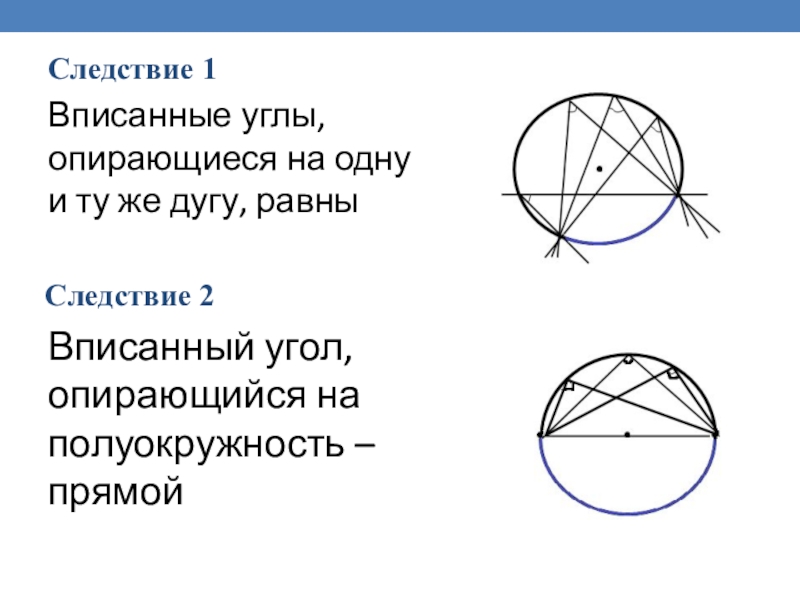
Слайд 21Следствие 1
Следствие 2
Вписанные углы, опирающиеся на одну и ту же дугу,
Вписанный угол, опирающийся на полуокружность – прямой
Слайд 22Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно
B
А
С
D
E
1
2
3
4
Теорема
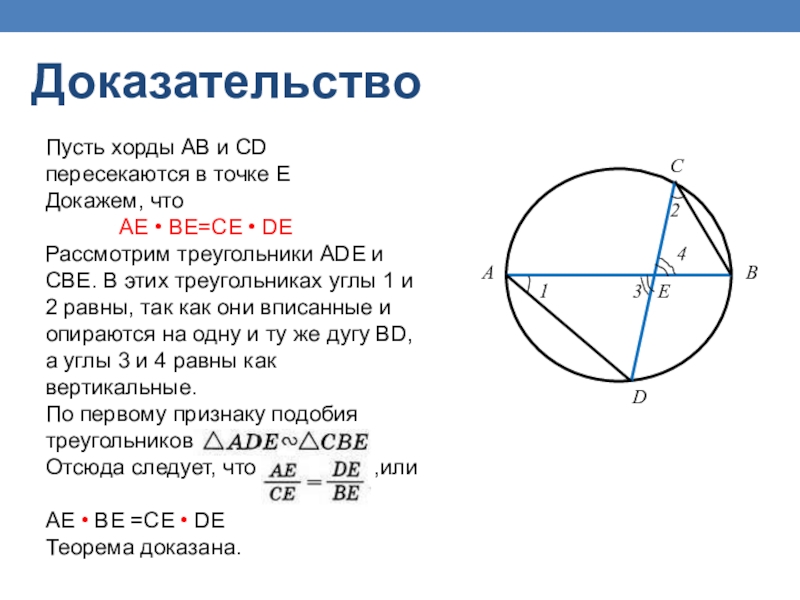
Слайд 23Пусть хорды АВ и CD пересекаются в точке Е
Докажем, что
Рассмотрим треугольники ADE и
СBE. В этих треугольниках углы 1 и 2 равны, так как они вписанные и опираются на одну и ту же дугу BD, а углы 3 и 4 равны как вертикальные.
По первому признаку подобия треугольников
Отсюда следует, что ,или
АЕ • ВЕ =СЕ • DE
Теорема доказана.
B
А
С
D
E
1
2
3
4
Доказательство