- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока-конкурса по математике по теме Тела вращения
Содержание
- 1. Презентация урока-конкурса по математике по теме Тела вращения
- 2. ЦЕЛИ УРОКА:Обобщить и систематизировать знания о
- 3. ВЫСТУПЛЕНИЕ КОМАНД УЧАСТНИКОВ КОНФЕРЕНЦИИ
- 4. Выступление команды ЦИЛИНДРЫ
- 5. План:1.Понятие цилиндра2.Прямой круговой цилиндр и его элементы3.Сечения
- 6. ЦИЛИНДРИЧЕСКОЕ ТЕЛО (Цилиндр) образующиеО1Оάβм1мrά||βLL1L=L1АА1Определение: цилиндрическим телом или цилиндром
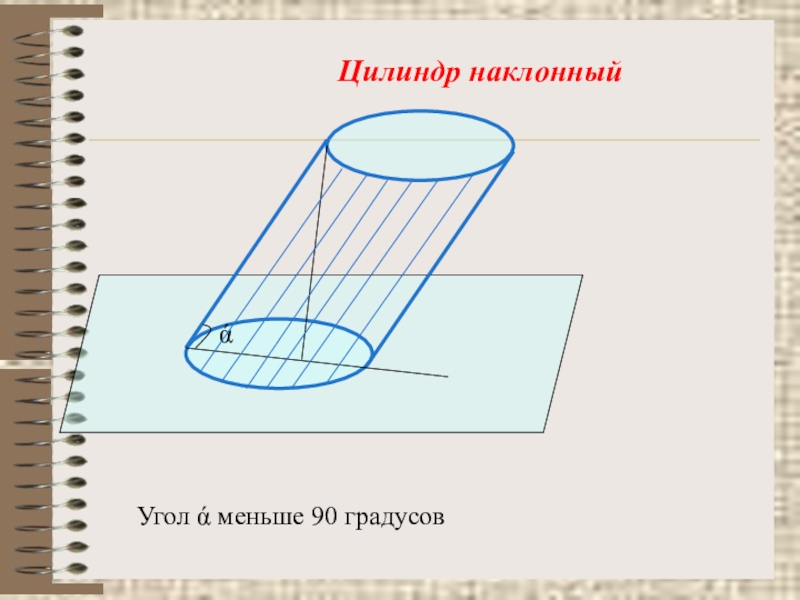
- 7. Угол ά меньше 90 градусовЦилиндр наклонный
- 8. ЦИЛИНДР прямой круговойОпределение: прямым круговым цилиндром называется
- 9. 3. Радиусом цилиндра называется радиус его основания4.
- 10. АDВСРис.1Прямой круговой цилиндр можно получить вращением прямоугольника
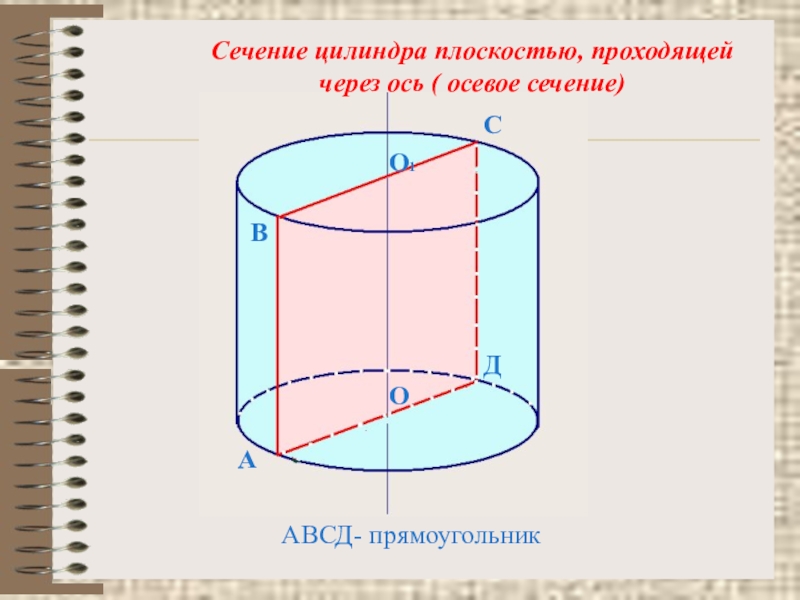
- 11. АВСДОО1Сечение цилиндра плоскостью, проходящей через ось ( осевое сечение)АВСД- прямоугольник
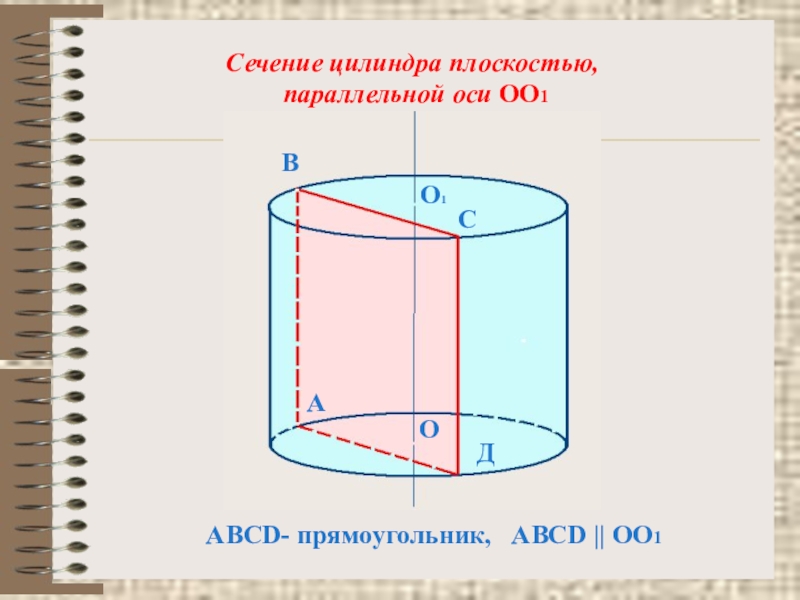
- 12. АВСДАВСD- прямоугольник, ABCD || ОО1О1Сечение цилиндра плоскостью, параллельной оси ОО1О
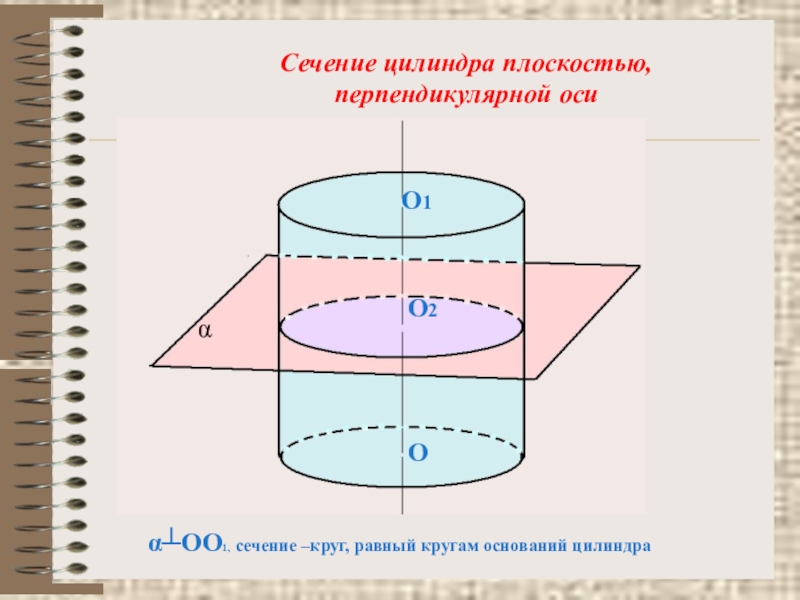
- 13. α┴OO1, сечение –круг, равный кругам оснований цилиндраСечение цилиндра плоскостью, перпендикулярной осиOO1O2α
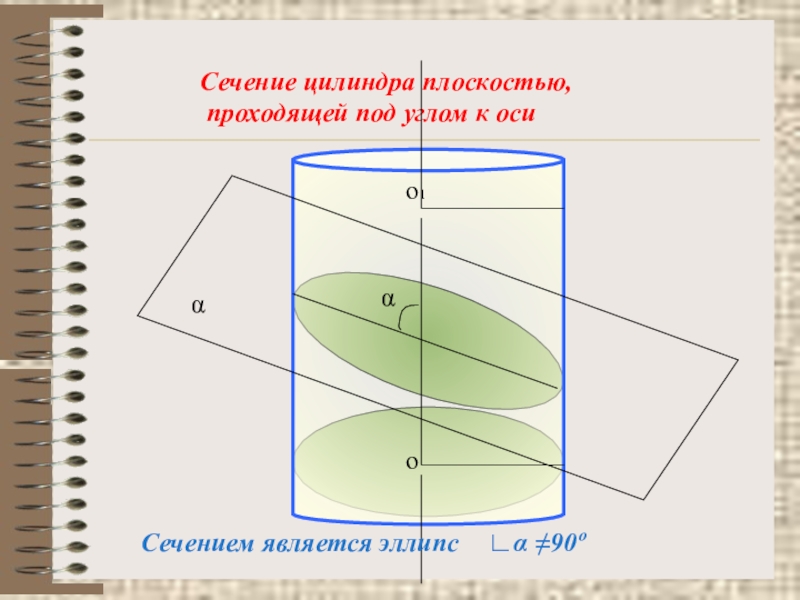
- 14. Сечение цилиндра плоскостью, проходящей под углом к осиСечением является эллипсα∟α ≠90ºоо1α
- 15. АВВ1А1- прямоугольникВА1В1А2πrhSбок = 2πrhSполн = Sбок+ 2
- 16. «Боковые и полные поверхности подобных цилиндров относятся
- 17. Цилиндры в архитектуре
- 18. Современная архитектура и цилиндры
- 19. Выступление команды КОНУСЫ
- 20. Историческая справка Конус в
- 21. Определение и основные элементыКонус – тело, полученное
- 22. Отрезок BC=2R – диаметр основания.Треугольник SBC-осевое сечение
- 23. Сечение конусаСекущая плоскость проходит через ось конуса (осевое сечение – равнобедренный треугольник)
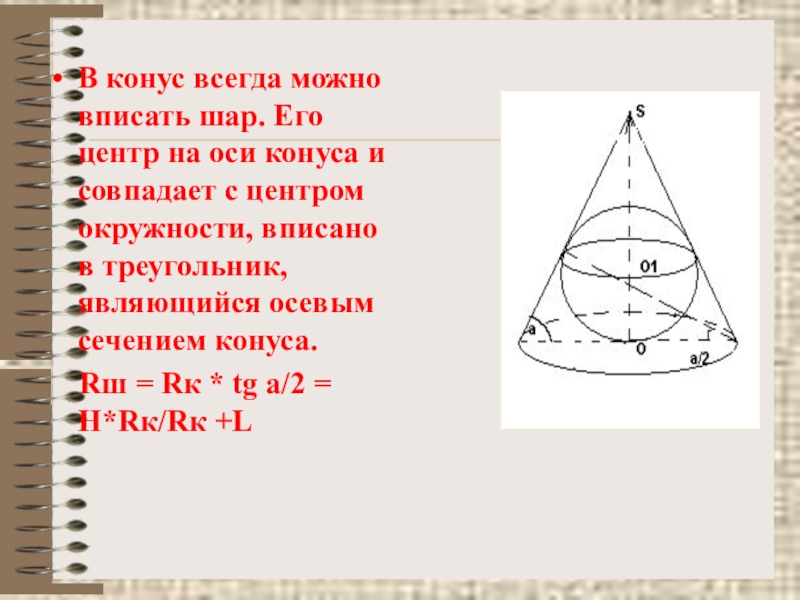
- 24. В конус всегда можно вписать шар. Его
- 25. Усечённый конусОснование исходного конуса и круг, полученный
- 26. Формулы нахождение площадей конуса
- 27. Площадь боковой поверхности усечённого
- 28. Объём конуса
- 29. Дополнительная информация о конусеВ геологии существует понятие
- 30. 3. «Конусами» называется семейство морских моллюсков подкласса
- 31. 4. По статистике на Земле ежегодно гибнет
- 32. Конусы вокруг нас
- 33. Выступление команды ШАРЫ
- 34. Сфера – множество точек пространства, расположенных на
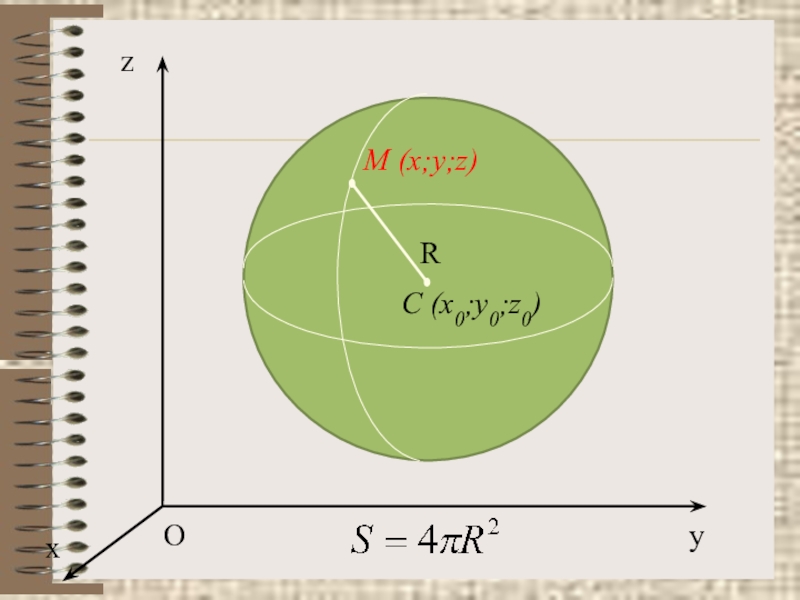
- 35. C (x0;y0;z0)RM (x;y;z)Ozyx
- 36. Расстояние от произвольной точки M (x;y;z) до точки С вычисляется по формуле:MC= (х-х0)2+(у-у0)2 +(z-z0)2
- 37. Уравнение сферы в прямоугольной системе Если точка
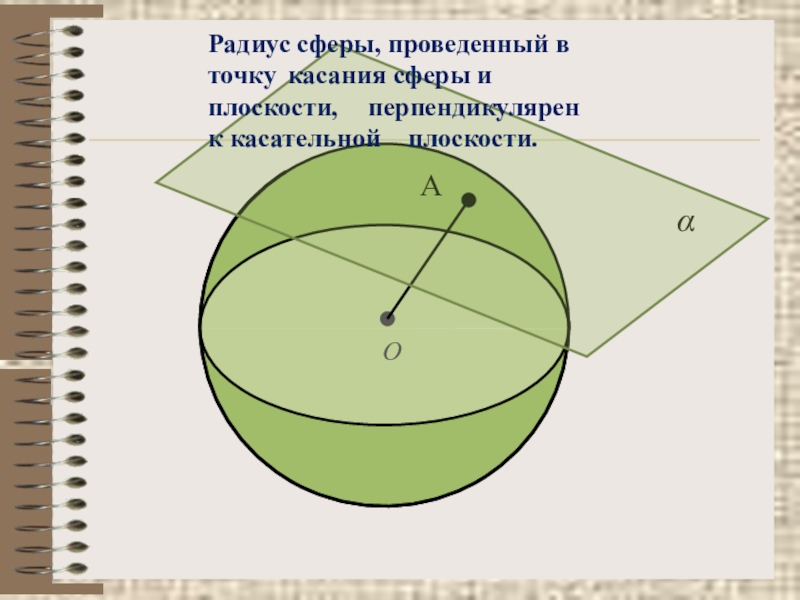
- 38. Оα АРадиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
- 39. Сферы и шары в природе
- 40. ВЫСТУПЛЕНИЕ КОМАНД УЧАСТНИКОВ КОНФЕРЕНЦИИ второй
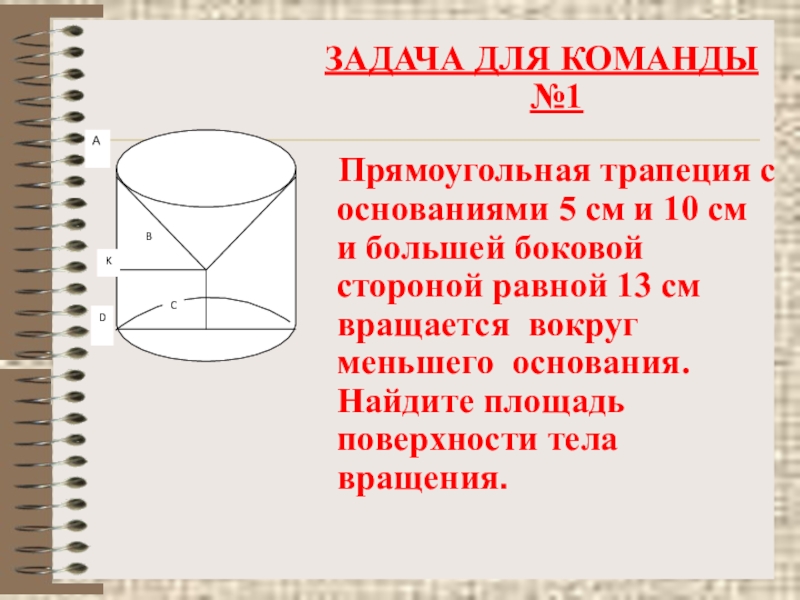
- 41. ЗАДАЧА ДЛЯ КОМАНДЫ №1 Прямоугольная
- 42. ЗАДАЧА ДЛЯ КОМАНДЫ № 2
- 43. ЗАДАЧА ДЛЯ КОМАНДЫ № 3
- 44. ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ1.Прямоугольный треугольник, катеты которого равны 15
- 45. ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ2.Площадь сечения шара плоскостью, проведённой через
- 46. ВЫСТУПЛЕНИЕ КОМАНД УЧАСТНИКОВ КОНФЕРЕНЦИИ третий
- 47. Слайд 47
- 48. Награждение победителей ПОДВЕДЕНИЕ ИТОГОВ
Слайд 1
КОНКУРС по математике
тема: Тела вращения
(ЦИЛИНДР, КОНУС, ШАР)
Преподаватель математики
ГАУ КО «Колледж предпринимательства»
ОСПОВАГ.В.
Слайд 2ЦЕЛИ УРОКА:
Обобщить и систематизировать знания о телах вращения, применение их
Развивать пространственное и логическое мышление, творческую деятельность, умение аргументировать свою речь.
Воспитывать культуру общения.
Слайд 3
ВЫСТУПЛЕНИЕ КОМАНД
УЧАСТНИКОВ КОНФЕРЕНЦИИ
первый тур: ПРЕДСТАВЛЕНИЕ.ОБМЕН
Команда № 1 «ЦИЛИНДРЫ»
Команда № 2 «КОНУСЫ»
Команда № 3 «ШАРЫ»
Слайд 5План:
1.Понятие цилиндра
2.Прямой круговой цилиндр и его элементы
3.Сечения цилиндра плоскостью
4.Площадь боковой и
поверхности цилиндра
5.Цилиндры вокруг нас
6. Самостоятельная работа
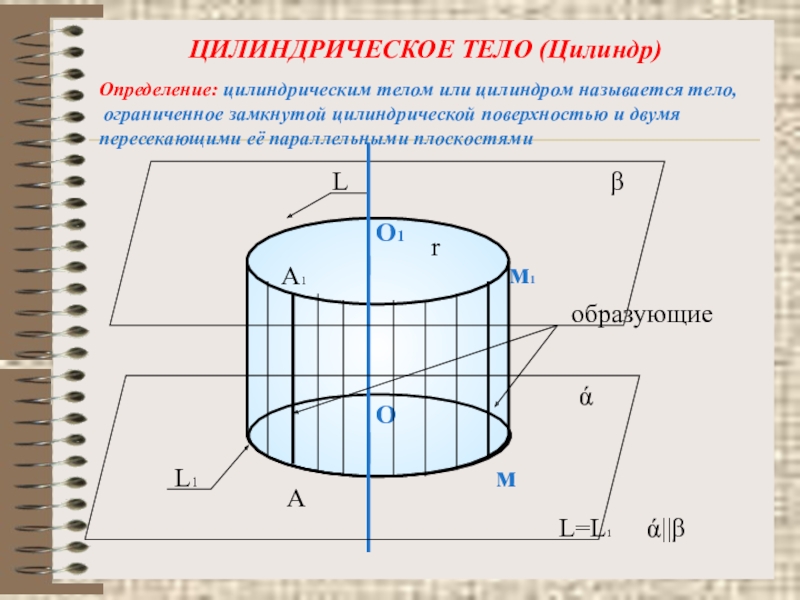
Слайд 6ЦИЛИНДРИЧЕСКОЕ ТЕЛО (Цилиндр)
образующие
О1
О
ά
β
м1
м
r
ά||β
L
L1
L=L1
А
А1
Определение: цилиндрическим телом или цилиндром называется тело,
ограниченное замкнутой
пересекающими её параллельными плоскостями
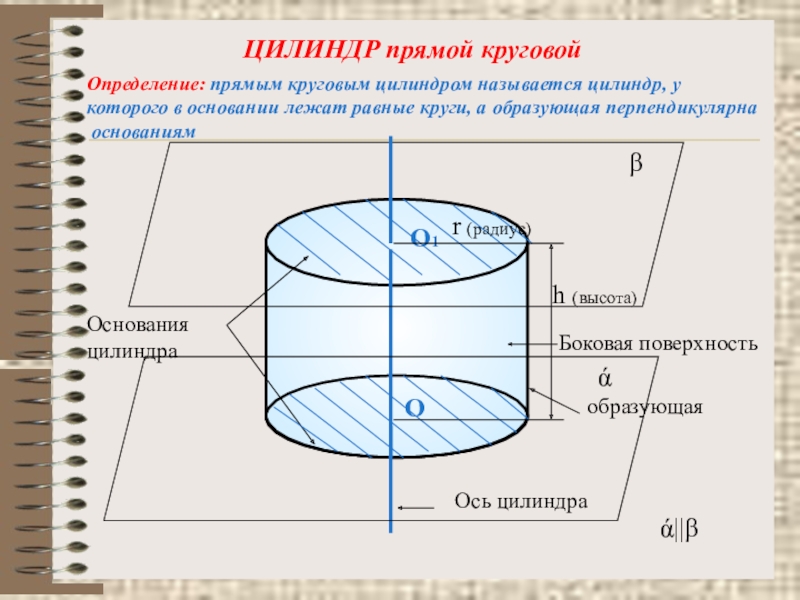
Слайд 8ЦИЛИНДР прямой круговой
Определение: прямым круговым цилиндром называется цилиндр, у
которого в
основаниям
ά||β
Слайд 93. Радиусом цилиндра называется радиус его основания
4. Высота цилиндра- расстояние между
в прямом цилиндре она совпадает с образующей
5. Ось цилиндра- прямая, проходящая через центры оснований,
Она параллельна образующим.
1. Боковой поверхностью цилиндра называется часть
цилиндрической поверхности, заключенная между
параллельными плоскостями
2. Основания- часть плоскостей, отсекаемых цилиндрической
поверхностью,
Слайд 10
А
D
В
С
Рис.1
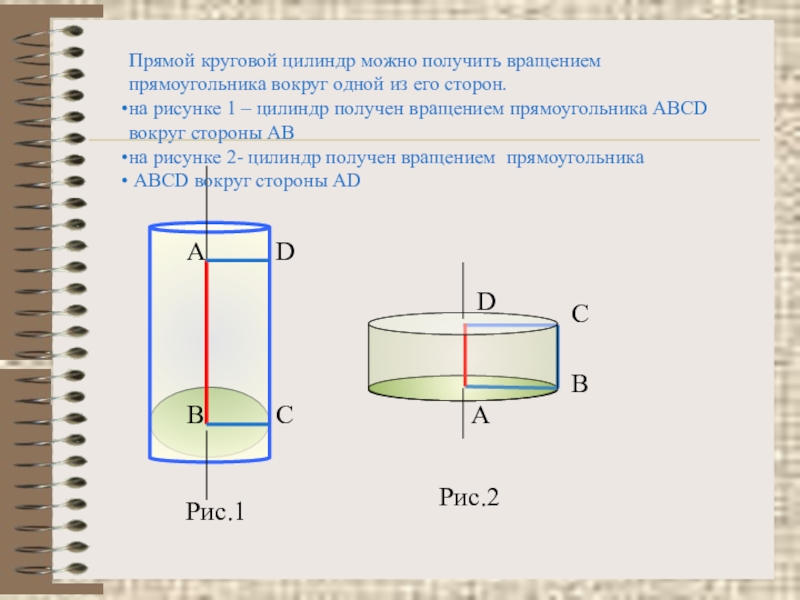
Прямой круговой цилиндр можно получить вращением
прямоугольника вокруг одной из его
на рисунке 1 – цилиндр получен вращением прямоугольника АВСD
вокруг стороны АВ
на рисунке 2- цилиндр получен вращением прямоугольника
АВСD вокруг стороны AD
Слайд 11
А
В
С
Д
О
О1
Сечение цилиндра плоскостью, проходящей
через ось ( осевое сечение)
АВСД- прямоугольник
Слайд 13α┴OO1, сечение –круг, равный кругам оснований цилиндра
Сечение цилиндра плоскостью,
перпендикулярной оси
O
O1
O2
α
Слайд 15АВВ1А1- прямоугольник
В
А1
В1
А
2πr
h
Sбок = 2πrh
Sполн = Sбок+ 2 Sосн => Sполн =
Боковая и полная поверхность цилиндра
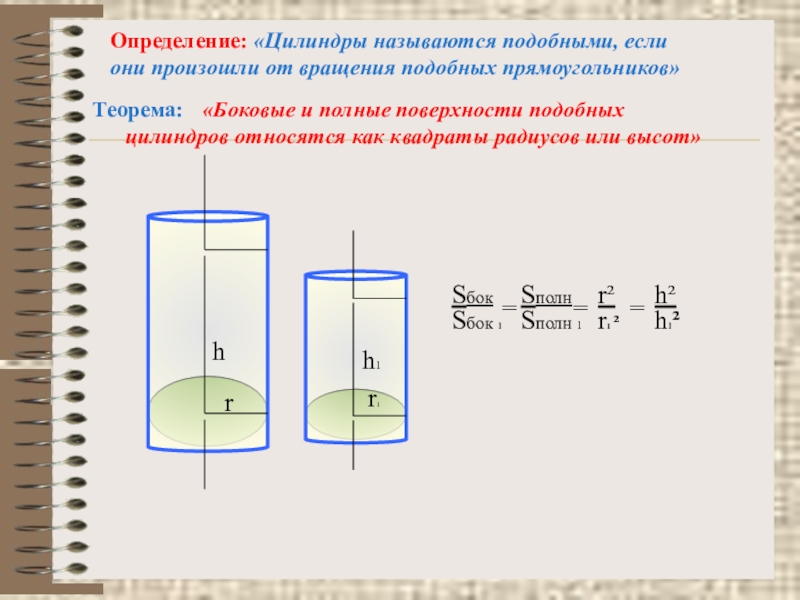
Слайд 16«Боковые и полные поверхности подобных
цилиндров относятся как квадраты радиусов или
Теорема:
Определение: «Цилиндры называются подобными, если
они произошли от вращения подобных прямоугольников»
Sбок 1
=
r1 ²
=
h1²
Sбок
r²
h²
=
Sполн
Sполн 1
Слайд 20Историческая справка
Конус в переводе с греческого «konos»
Много сделала для геометрии школа Платона. Ей принадлежат: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
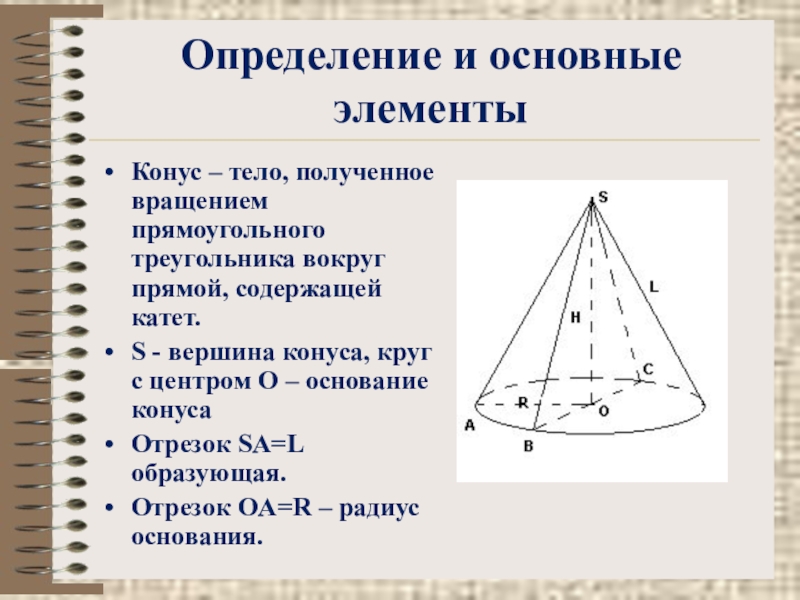
Слайд 21Определение и основные элементы
Конус – тело, полученное вращением прямоугольного треугольника вокруг
S - вершина конуса, круг с центром О – основание конуса
Отрезок SA=L образующая.
Отрезок OA=R – радиус основания.
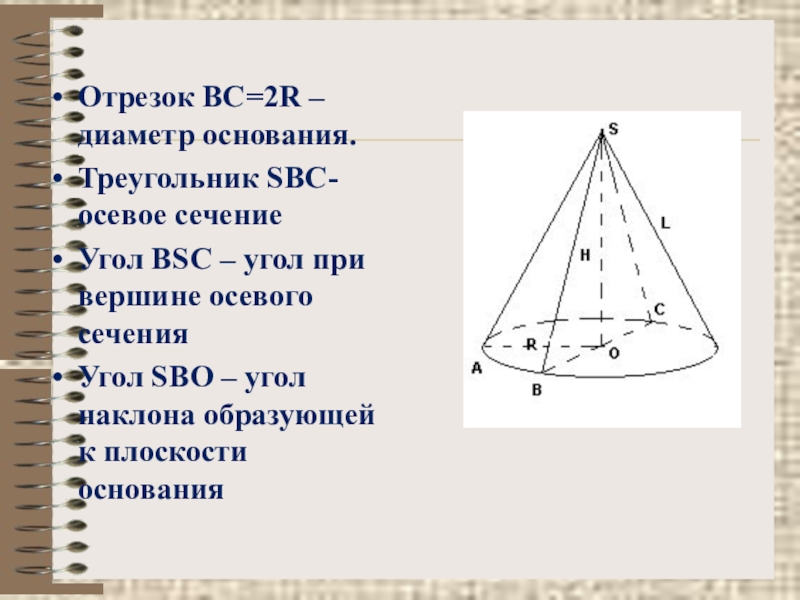
Слайд 22Отрезок BC=2R – диаметр основания.
Треугольник SBC-осевое сечение
Угол BSC – угол
Угол SBO – угол наклона образующей к плоскости основания
Слайд 23
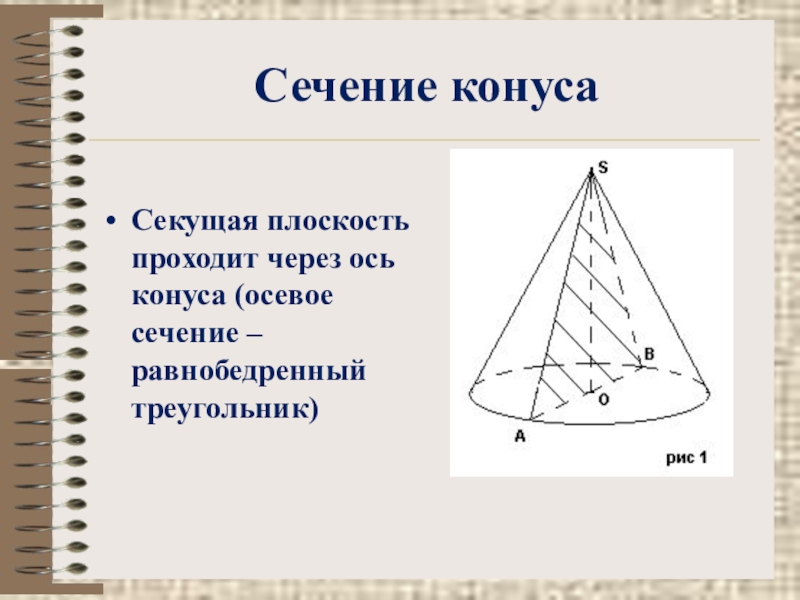
Сечение конуса
Секущая плоскость проходит через ось конуса (осевое сечение – равнобедренный
Слайд 24В конус всегда можно вписать шар. Его центр на оси конуса
Rш = Rк * tg a/2 = H*Rк/Rк +L
Слайд 25Усечённый конус
Основание исходного конуса и круг, полученный в сечении этого конуса
Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью
Отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса.
Все образующие усечённого конуса равны друг другу.
Слайд 26Формулы
нахождение площадей конуса
Площадь полной поверхности конуса:
Площадь боковой поверхности:
Sбок=Sкруг сектора=Пчl
Площадь осевого сечения:
Sсеч=Rh
Слайд 27 Площадь боковой поверхности усечённого конуса равна произведению полусуммы
Sбок=П(r+r1)l
Слайд 29Дополнительная информация о конусе
В геологии существует понятие «конус выноса». Это форма
В биологии есть понятие «конус нарастания». Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.
Слайд 303. «Конусами» называется семейство морских моллюсков подкласса переднежаберных. Конусов свыше 500
Слайд 314. По статистике на Земле ежегодно гибнет от разрядов молний 6
Слайд 34Сфера – множество точек пространства, расположенных
на заданном расстоянии от центра
Тело, ограниченное
Сфера – граница шара
Слайд 36 Расстояние от произвольной точки M (x;y;z) до точки С вычисляется
MC= (х-х0)2+(у-у0)2 +(z-z0)2
Слайд 37Уравнение сферы в прямоугольной системе
Если точка М лежит на данной
(х-х0)2+(у-у0)2 +(z-z0)2 = R2
Слайд 38
О
α
А
Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен
Слайд 40
ВЫСТУПЛЕНИЕ КОМАНД
УЧАСТНИКОВ КОНФЕРЕНЦИИ
второй тур ДЕМОНСТРАЦИЯ ЗНАНИЙ
Команда № 1 «ЦИЛИНДРЫ»
Команда № 2
Команда № 3 «ШАРЫ»
Слайд 41ЗАДАЧА ДЛЯ КОМАНДЫ №1
Прямоугольная трапеция с основаниями 5
K
D
А
B
C
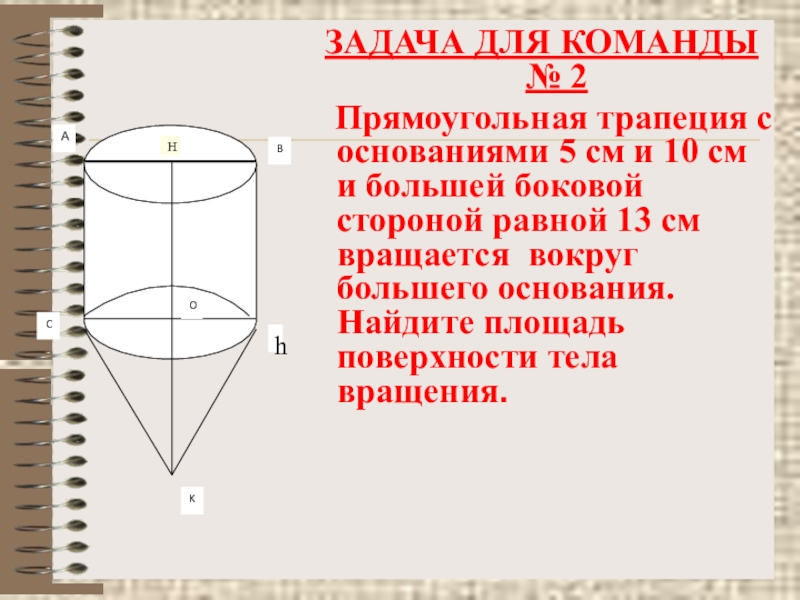
Слайд 42ЗАДАЧА ДЛЯ КОМАНДЫ № 2
Прямоугольная трапеция с основаниями
А
B
C
h
O
K
H
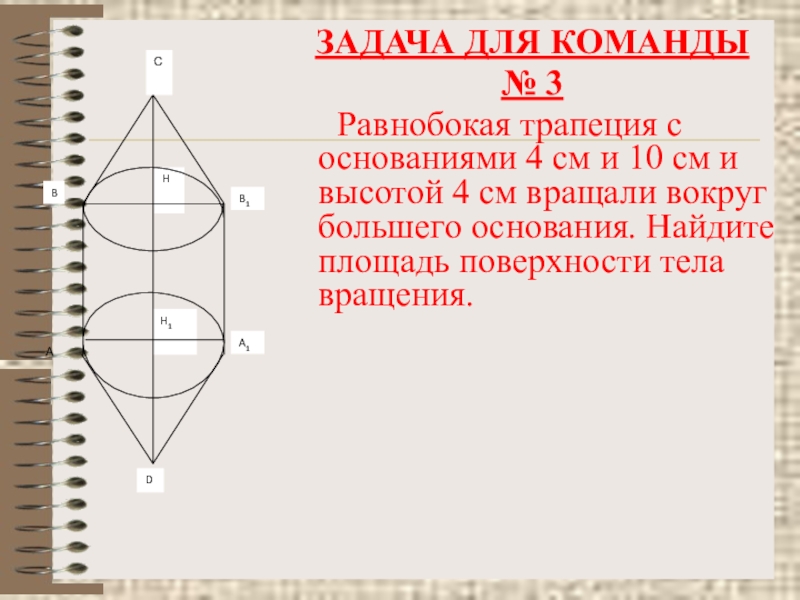
Слайд 43ЗАДАЧА ДЛЯ КОМАНДЫ
№ 3
Равнобокая трапеция с основаниями
B
B1
D
A1
Слайд 44ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ
1.Прямоугольный треугольник, катеты которого равны 15 см и 8 см
Слайд 45ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ
2.Площадь сечения шара плоскостью, проведённой через диаметра под углом 60°
Найдите площадь поверхности шара.
3.Прямоугольник АВСD вращается вокруг стороны АВ. Найдите площадь полной поверхности тела вращения, если ВС = 3м, ВD=5м.
Слайд 46
ВЫСТУПЛЕНИЕ КОМАНД
УЧАСТНИКОВ КОНФЕРЕНЦИИ
третий тур: ОБМЕН МНЕНИЯМИ.
Команда № 1 «ЦИЛИНДРЫ»
Команда № 2 «КОНУСЫ»
Команда № 3 «ШАРЫ»