- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока геометрии на тему Свойства равнобедренного треугольника
Содержание
- 1. Презентация урока геометрии на тему Свойства равнобедренного треугольника
- 2. Цели урока:Образовательные: 1. Формирование умения решать задачи
- 3. План урока:
- 4. Поверка домашнего задания.№ 119.
- 5. Устная работаДоказать:
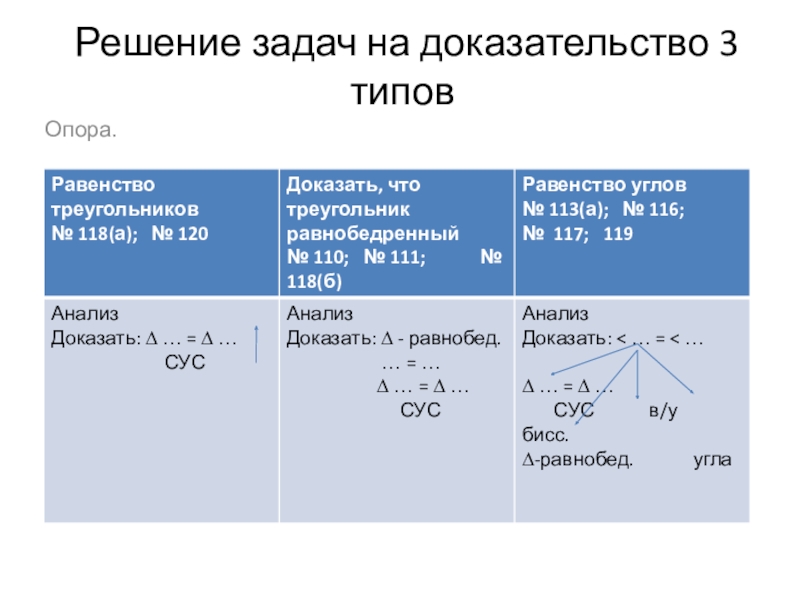
- 6. Решение задач на доказательство 3 типовОпора.
- 7. № 111.
- 8. № 118
- 9. №113
- 10. Самостоятельная работаНа основании АС равнобедренного треугольника АВС
Цели урока:Образовательные: 1. Формирование умения решать задачи на доказательство, применяя свойства равнобедренного треугольника; 2.Продолжить формирование навыков анализа задач.Развивающее: 1. Содействовать в ходе урока формированию культуры устной и письменной речи; 2. Развитие умений преодолевать трудности в учении.Воспитательные:
Слайд 2Цели урока:
Образовательные: 1. Формирование умения решать задачи на доказательство, применяя свойства
равнобедренного треугольника; 2.Продолжить формирование навыков анализа задач.
Развивающее: 1. Содействовать в ходе урока формированию культуры устной и письменной речи; 2. Развитие умений преодолевать трудности в учении.
Воспитательные: воспитание нравственного качества – трудолюбия.
Развивающее: 1. Содействовать в ходе урока формированию культуры устной и письменной речи; 2. Развитие умений преодолевать трудности в учении.
Воспитательные: воспитание нравственного качества – трудолюбия.
Слайд 3План урока:
1.
Проверка д/з.
2. Устная работа.
3. Решение задач.
4. Обучающая к/р.
5. Итог урока. Задание на дом.
2. Устная работа.
3. Решение задач.
4. Обучающая к/р.
5. Итог урока. Задание на дом.
Слайд 4Поверка домашнего задания.
№ 119.
а) Дано: ΔДЕК – равнобедренный
ДК – основание
ЕF -биссектриса
ДК = 16см
<ДЕF = 43°
Найти: КЕ; <ДЕК; <ЕFД
Решение: 1. ЕF – биссектриса; следовательно < ДЕК = < ДЕF + < FЕК = 43°+43°=86°
2. В равнобедренном треугольнике биссектриса является высотой, значит <ЕFД=90 °.
3. В равнобедренном треугольнике биссектриса является медианой, поэтому ДF= FК , FК =1/2ДК=1/2 ∙ 16 = 8(см).
Ответ: 8 см.
ДК – основание
ЕF -биссектриса
ДК = 16см
<ДЕF = 43°
Найти: КЕ; <ДЕК; <ЕFД
Решение: 1. ЕF – биссектриса; следовательно < ДЕК = < ДЕF + < FЕК = 43°+43°=86°
2. В равнобедренном треугольнике биссектриса является высотой, значит <ЕFД=90 °.
3. В равнобедренном треугольнике биссектриса является медианой, поэтому ДF= FК , FК =1/2ДК=1/2 ∙ 16 = 8(см).
Ответ: 8 см.
Д
К
F
Е
43°
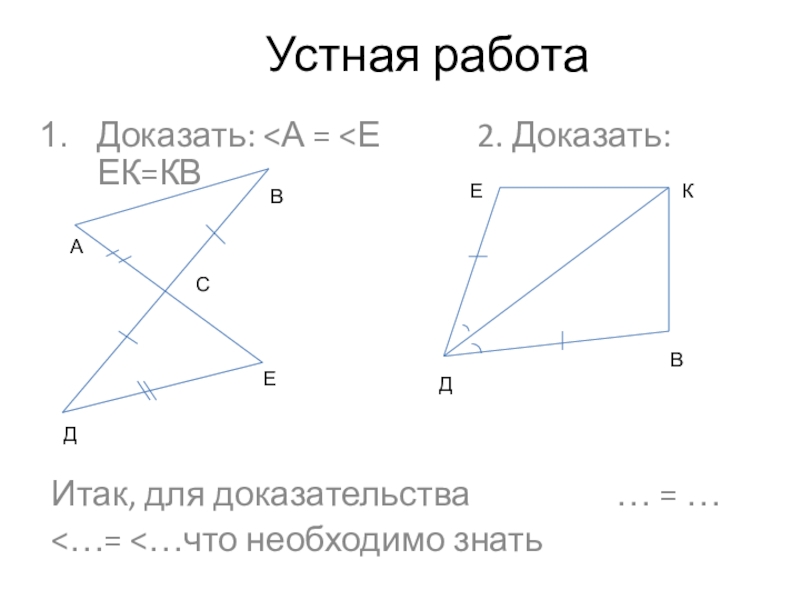
Слайд 5Устная работа
Доказать:
Доказать:ЕК=КВ
Итак, для доказательства … = …
<…= <…что необходимо знать
Итак, для доказательства … = …
<…= <…что необходимо знать
А
В
Е
С
Д
Д
В
Е
К
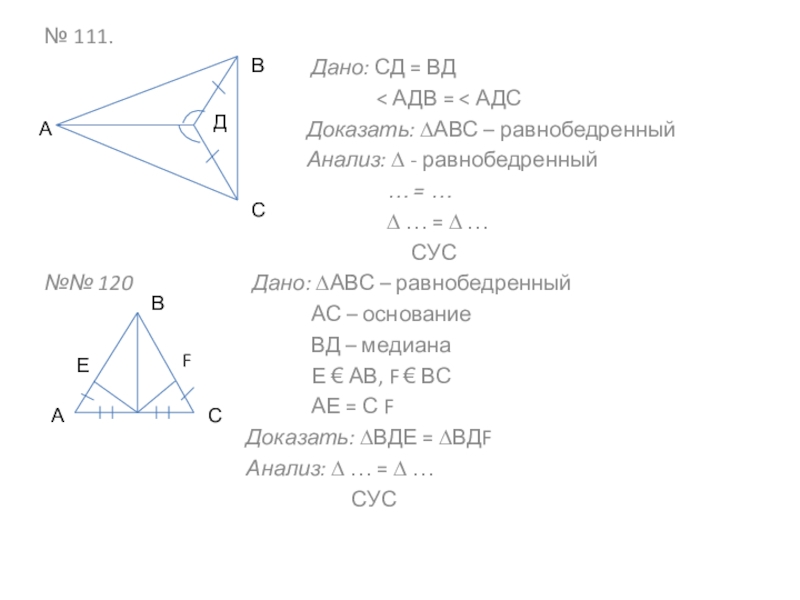
Слайд 7№ 111.
Дано: СД = ВД
< АДВ = < АДС
Доказать: ∆АВС – равнобедренный
Анализ: ∆ - равнобедренный
… = …
∆ … = ∆ …
СУС
№№ 120 Дано: ∆АВС – равнобедренный
АС – основание
ВД – медиана
Е € АВ, F € ВС
АЕ = С F
Доказать: ∆ВДЕ = ∆ВДF
Анализ: ∆ … = ∆ …
СУС
< АДВ = < АДС
Доказать: ∆АВС – равнобедренный
Анализ: ∆ - равнобедренный
… = …
∆ … = ∆ …
СУС
№№ 120 Дано: ∆АВС – равнобедренный
АС – основание
ВД – медиана
Е € АВ, F € ВС
АЕ = С F
Доказать: ∆ВДЕ = ∆ВДF
Анализ: ∆ … = ∆ …
СУС
В
С
А
Д
А
С
В
Е
F
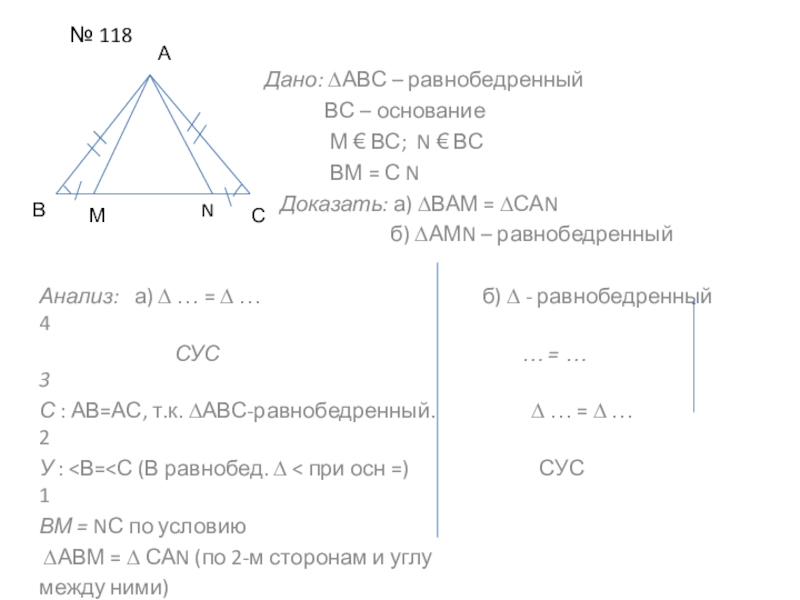
Слайд 8№ 118
Дано: ∆АВС – равнобедренный
ВС – основание
М € ВС; N € ВС
ВМ = С N
Доказать: а) ∆ВАМ = ∆САN
б) ∆АМN – равнобедренный
Анализ: а) ∆ … = ∆ … б) ∆ - равнобедренный 4
СУС … = … 3
С : АВ=АС, т.к. ∆АВС-равнобедренный. ∆ … = ∆ … 2
У : <В=<С (В равнобед. ∆ < при осн =) СУС 1
ВМ = NС по условию
∆АВМ = ∆ САN (по 2-м сторонам и углу
между ними)
ВС – основание
М € ВС; N € ВС
ВМ = С N
Доказать: а) ∆ВАМ = ∆САN
б) ∆АМN – равнобедренный
Анализ: а) ∆ … = ∆ … б) ∆ - равнобедренный 4
СУС … = … 3
С : АВ=АС, т.к. ∆АВС-равнобедренный. ∆ … = ∆ … 2
У : <В=<С (В равнобед. ∆ < при осн =) СУС 1
ВМ = NС по условию
∆АВМ = ∆ САN (по 2-м сторонам и углу
между ними)
В
М
N
С
А
Слайд 9№113
Дано: М и Р лежат в одну сторону от прямой в
МN в, РQ в.
т. О – середина NQ, NО = ОQ
Доказать: <ОМР = <ОРМ
Анализ: < … = < … 4 1) ∆МNО и ∆РQО
∆ - равнобедренный 3 С : МN = РQ (по условию)
… = … 2 У : < N = < Q = 90°, т.к. МN в, РQ в.
∆ … = ∆ … 1 С : NО = ОQ (по условию)
∆МNО = ∆РQО (по двум сторонам и
углу между ними)
2) Из равенство ∆-ов, что ОМ=ОР,
значит ∆МОР - равнобедренный.
3) По свойству равнобедренного ∆-ка
<ОМР = <ОРМ
МN в, РQ в.
т. О – середина NQ, NО = ОQ
Доказать: <ОМР = <ОРМ
Анализ: < … = < … 4 1) ∆МNО и ∆РQО
∆ - равнобедренный 3 С : МN = РQ (по условию)
… = … 2 У : < N = < Q = 90°, т.к. МN в, РQ в.
∆ … = ∆ … 1 С : NО = ОQ (по условию)
∆МNО = ∆РQО (по двум сторонам и
углу между ними)
2) Из равенство ∆-ов, что ОМ=ОР,
значит ∆МОР - равнобедренный.
3) По свойству равнобедренного ∆-ка
<ОМР = <ОРМ
N
Q
O
Р
М
Слайд 10Самостоятельная работа
На основании АС равнобедренного треугольника АВС отмечены равные отрезки АД
и СЕ
«3» – а) Доказать, что ∆ВАД = ∆ВСЕ
«4» – б) Доказать, что ∆ВДЕ - равнобедренный
«5» – в) Найти <ВЕД, если <АДВ = 140°
«3» – а) Доказать, что ∆ВАД = ∆ВСЕ
«4» – б) Доказать, что ∆ВДЕ - равнобедренный
«5» – в) Найти <ВЕД, если <АДВ = 140°