- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад тест по теме Признаки подобия треугольников выполненная школьником
Содержание
- 1. Презентация тест по теме Признаки подобия треугольников выполненная школьником
- 2. Слайд 2
- 3. Если две стороны одного треугольника пропорциональны двум
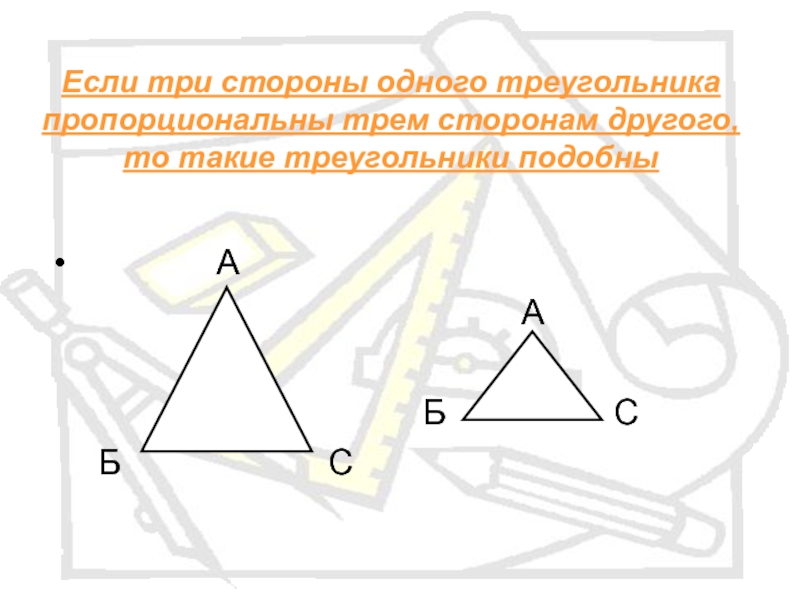
- 4. Если три стороны одного треугольника пропорциональны трем
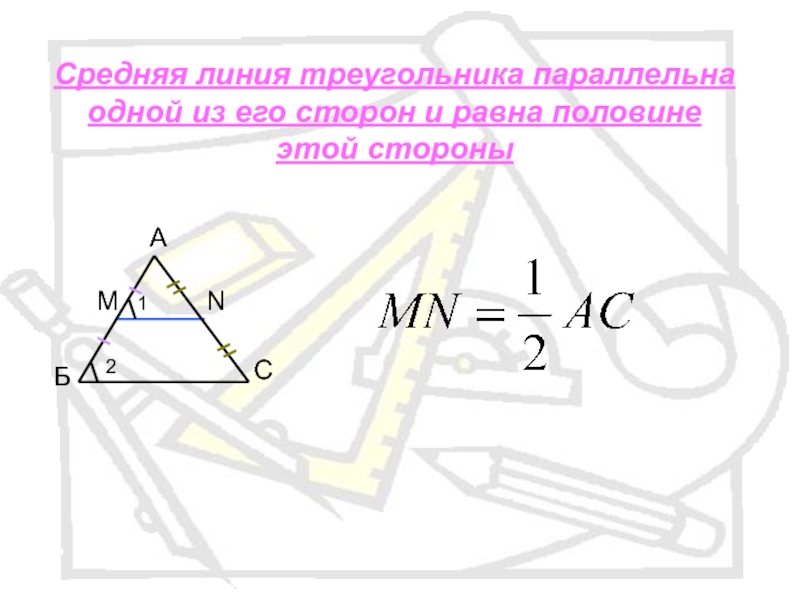
- 5. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороныАБ
- 6. Медианы Треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершиныАСBB1A1
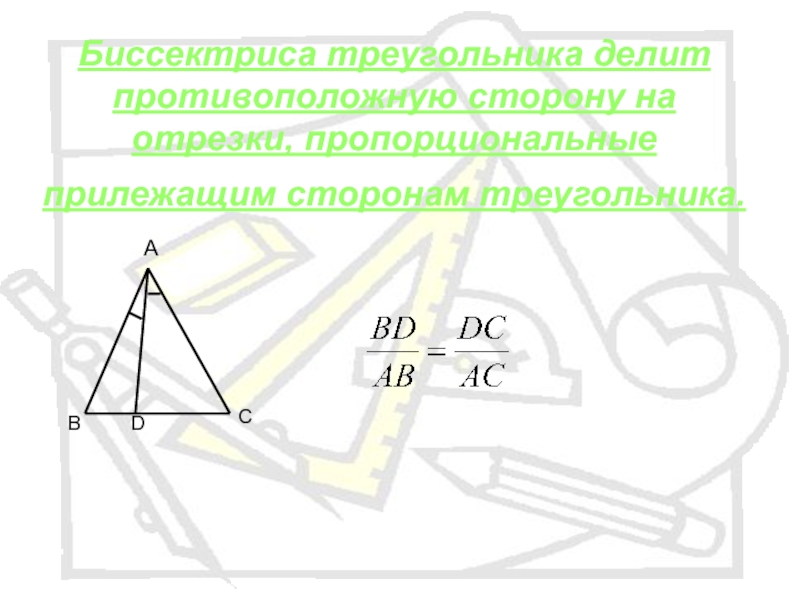
- 7. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника. BCDA
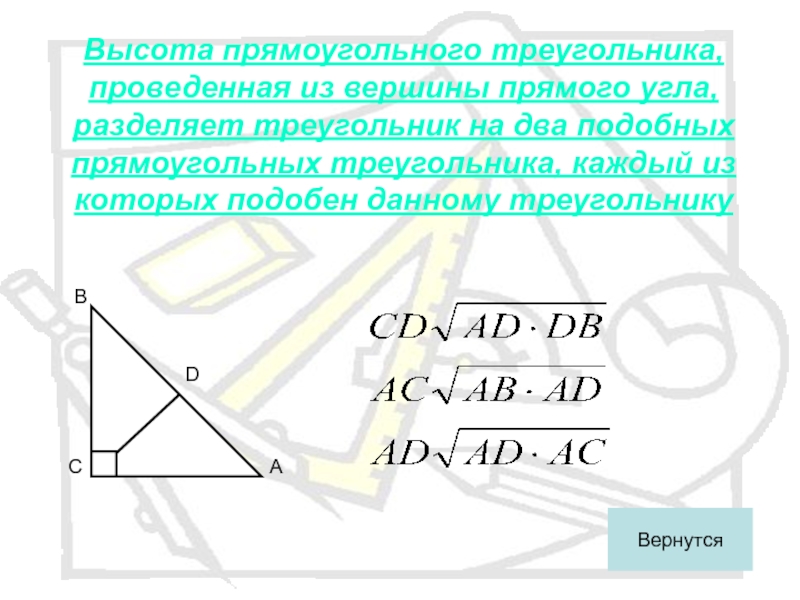
- 8. Высота прямоугольного треугольника, проведенная из вершины прямого
- 9. Основание высоты прямоугольного треугольника, опущенной на гипотенузу,
- 10. Периметр одного треугольника составляет периметра
- 11. Продолжение боковых сторон AB и CD трапеции
- 12. В треугольнике ABC проведен отрезок DE, параллельный
- 13. У двух равнобедренных треугольников углы между боковыми
- 14. Правильно В треугольнике ABC
- 15. ВернутсяПодумайВернутся
- 16. Пусть АВ=x, тогда
- 17. ПодумайВернутся
- 18. Рассмотрим треугольник AED и
- 19. ПодумайВернутся
- 20. Треугольник АВС~DBE тогда:Далее BD=AB-AD, так что 240=320-20AD, 20AD-80; AD=4Ответ:4смПравильноСледующая задача
- 21. ПодумайВернутся
- 22. Пусть треугольник ABC и А1В1С1 угол В = углу В1, АС=8, А1С1=10, А1В1=17см.Тогда треугольник АВС~ А1В1С1,значитОтвет:13,6ПравильноДалее
- 23. ПодумайВернутся
- 24. Молодцы
Слайд 2 А
А
Б С С Б
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны
Слайд 3Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и
А
А
Б С
С Б
Слайд 4Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие
А
А
Б С
Б С
Слайд 6Медианы Треугольника пересекаются в одной точке, которая делит каждую медиану в
А
С
B
B1
A1
Слайд 7Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
B
C
D
A
Слайд 8Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на
D
C
A
B
Вернутся
Слайд 9Основание высоты прямоугольного треугольника, опущенной на гипотенузу, делит ее на отрезки
а)AC=20,CB=15,AB=50 в)AC=2,CB=10,АB=13
б)AC=15,CB=20,AB=25 г)AC=4,CB=20,AB=26
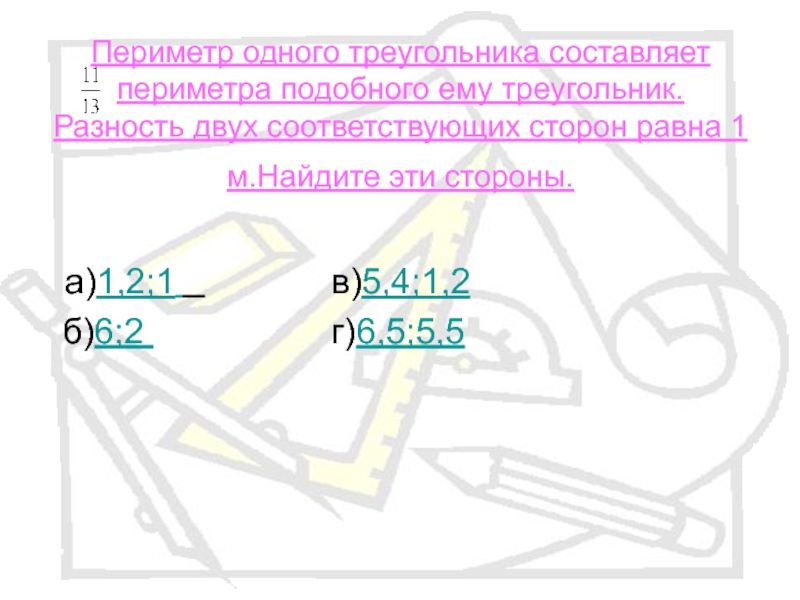
Слайд 10Периметр одного треугольника составляет периметра подобного ему треугольник. Разность
а)1,2;1 в)5,4;1,2
б)6;2 г)6,5;5,5
Слайд 11Продолжение боковых сторон AB и CD трапеции ABCD пересекаются в точке
а) АЕ=15 DE=18 в) AE=10DE=18
б) AE=23 DE=20 г) AE=19DE=11
Слайд 12В треугольнике ABC проведен отрезок DE, параллельный стороне AC(конец D отрезка
а)8см в) 4см
б)3см г) 12см
Слайд 13У двух равнобедренных треугольников углы между боковыми сторонами равны. Боковая сторона
а)12 в)3
б)13,6 г)2,3
Слайд 14
Правильно
В треугольнике ABC
AD=9, DB=16 треугольник ACD ~ CBD(так как уголCDA
= углу CDB =90* и угол ACD=90-угол A = углу B.)
Значит =AD*DB
Далее из треугольника ACD по теореме Пифагора имеем: Из треугольника CDB по теореме Пифагора имеем:
AB=AD+DB=9+16=25 Ответ:AC=15 CB=20 AB=25
Следующая задача
Слайд 18 Рассмотрим треугольник AED и BEC. Так как AD
50+10BE=15BE 5BE=50 BE=10
Тогда AE=AB+BE=10+5=15
Аналогично из подобия треугольников AED BEC имеем:
А, так как DE=CD+CE, то
15СЕ=60+10СЕ 5СЕ=60 СЕ=12 DE=CE+CD=6+12=18
Ответ AE=15 DE=18
Правильно
Следующая задача
Слайд 20Треугольник АВС~DBE тогда:
Далее BD=AB-AD, так что
240=320-20AD, 20AD-80; AD=4
Ответ:4см
Правильно
Следующая задача
Слайд 22Пусть треугольник ABC и А1В1С1 угол В = углу В1, АС=8,
Ответ:13,6
Правильно
Далее