- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Решение задач по теме Векторы 9 класс Атанасян
Содержание
- 1. Презентация Решение задач по теме Векторы 9 класс Атанасян
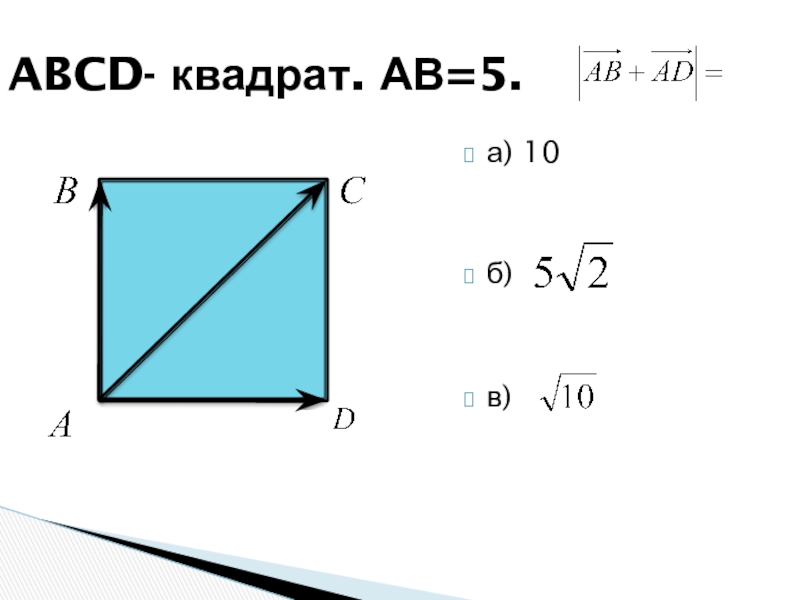
- 2. а) 10б)в)ABCD- квадрат. АВ=5.
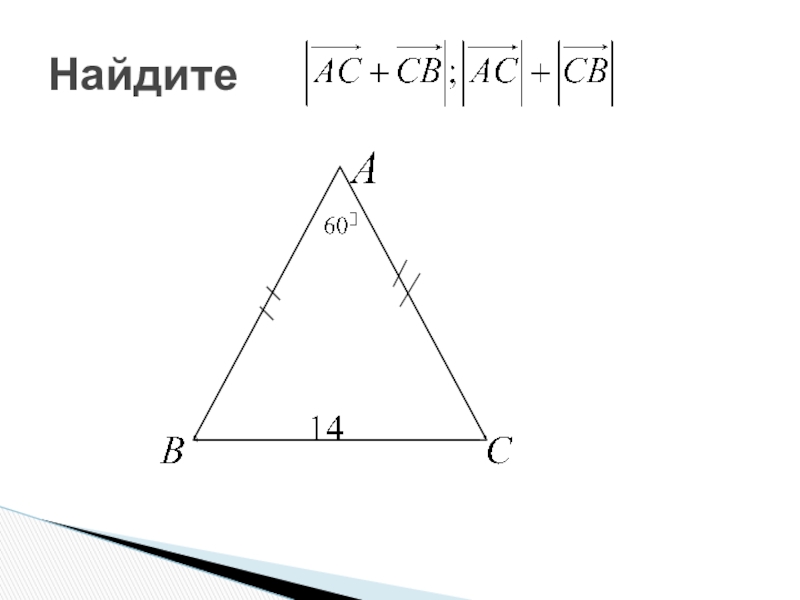
- 3. Найдите
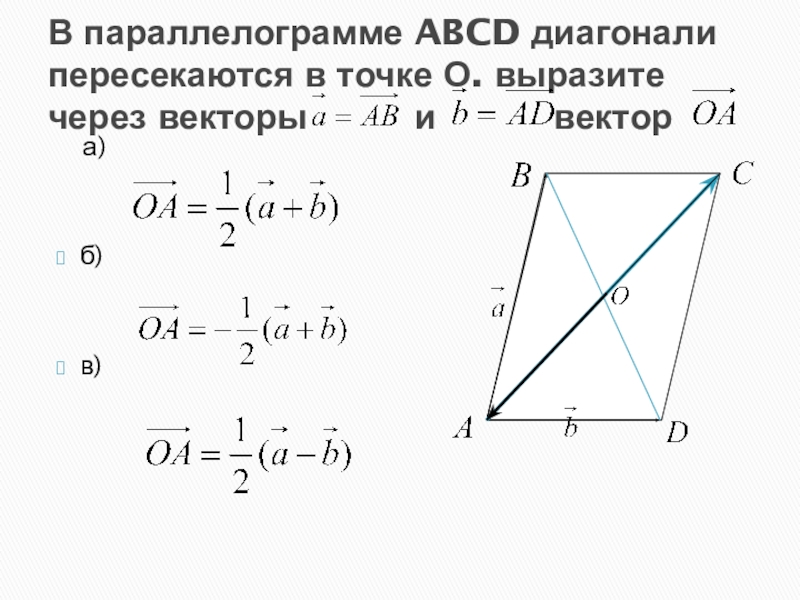
- 4. В параллелограмме ABCD диагонали пересекаются в точке
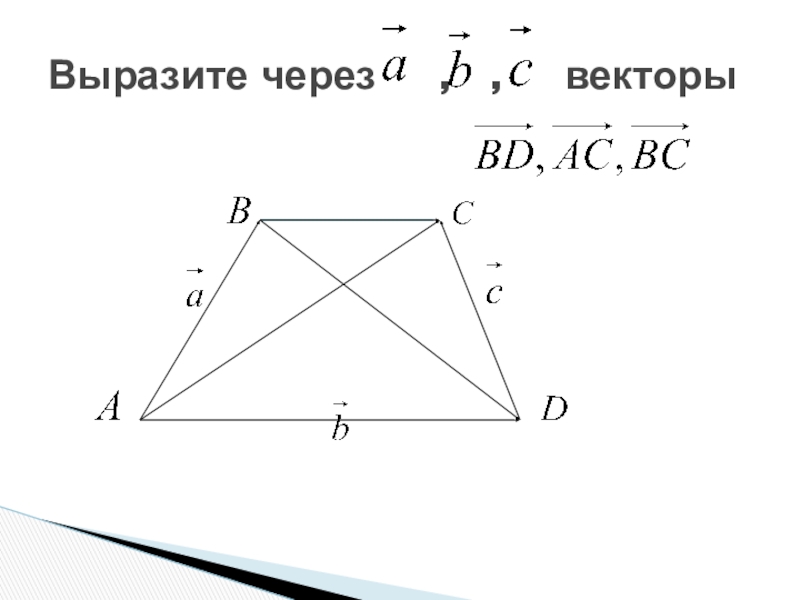
- 5. Выразите через , , векторы
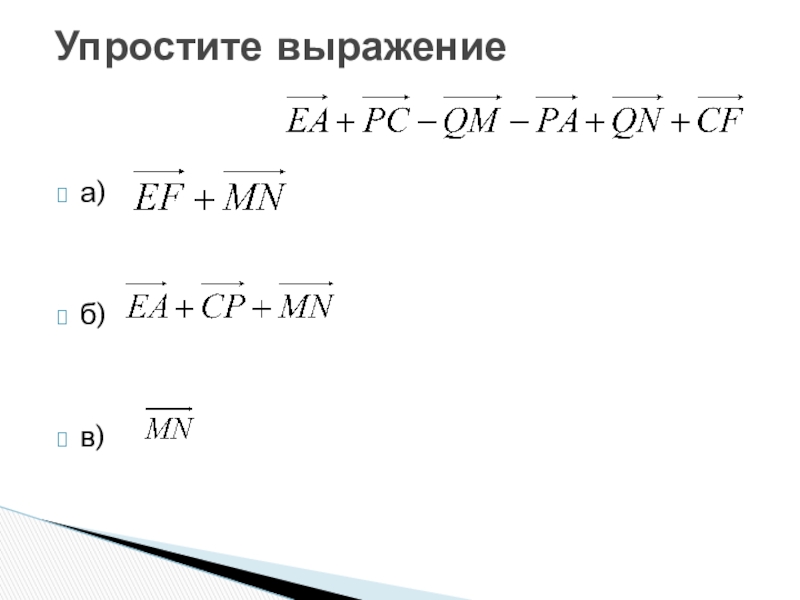
- 6. а)б)в)Упростите выражение
- 7. Применение векторов к решению задачУпростите выражение2. Из условия найдите вектор .
- 8. ABCD- параллелограмм. BE:EC=3:2, DK:KC=1:4. Выразите через
- 9. Таблица перевода с «геометрического» языка на « векторный»
- 10. № 768; 771;Задание на сампо:
- 11. Применение векторов к решению задачЗадача 1.Точка С
- 12. Применение векторов к решению задачРешение: По правилу
- 13. Применение векторов к решению задачЗадача 2.Доказать, что
- 14. Применение векторов к решению задачРешение:
- 15. Применение векторов к решению задач
- 16. Применение векторов к решению задачЗадание на сампо:П.84, № 769, 782, 784,786
а) 10б)в)ABCD- квадрат. АВ=5.
Слайд 4В параллелограмме ABCD диагонали пересекаются в точке О. выразите через векторы
и вектор
а)
б)
в)
Слайд 11Применение векторов к решению задач
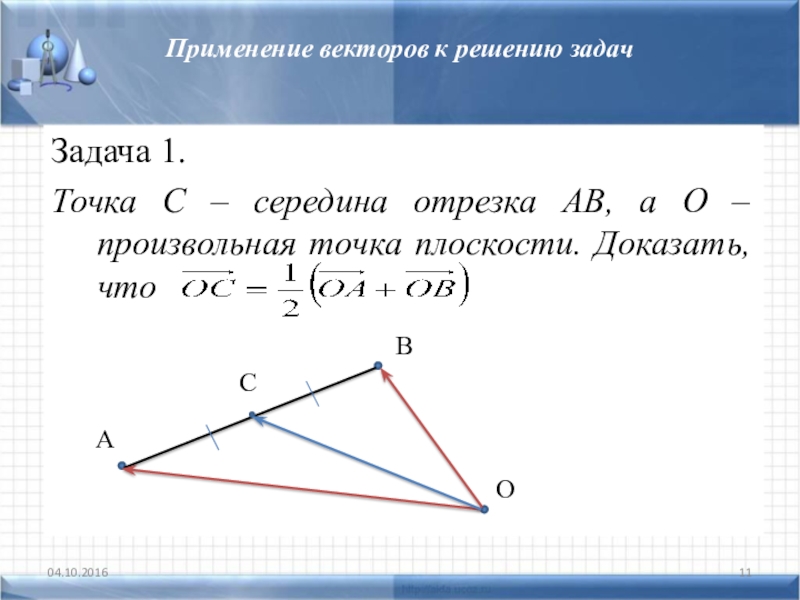
Задача 1.
Точка С – середина отрезка АВ,
а О – произвольная точка плоскости. Доказать, что
В
О
С
А
Слайд 12Применение векторов к решению задач
Решение: По правилу треугольника
. Складывая эти равенства,
получаем
Так как С – середина отрезка АВ, то .
Таким образом , или
получаем
Так как С – середина отрезка АВ, то .
Таким образом , или
Слайд 13Применение векторов к решению задач
Задача 2.
Доказать, что прямая, проведённая через середины
оснований трапеции, проходит через точку пересечения продолжений боковых сторон
Слайд 14Применение векторов к решению задач
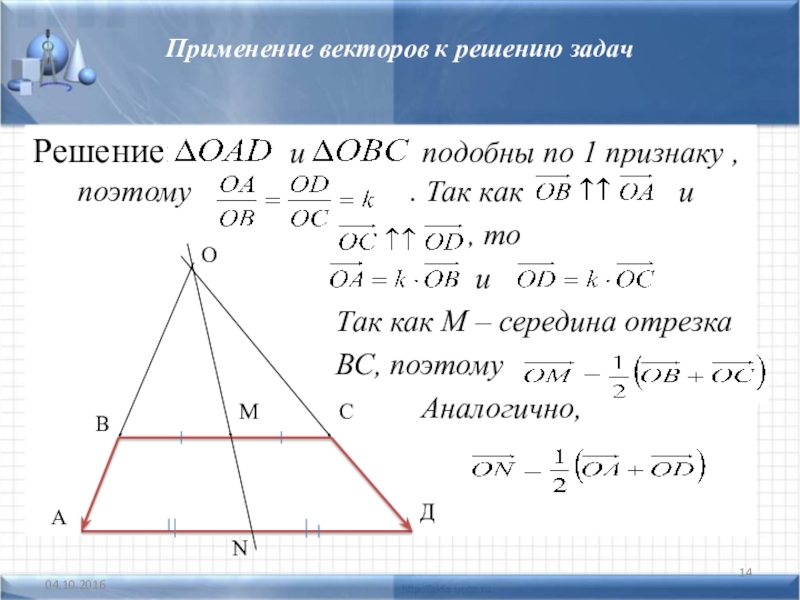
Решение:
и подобны по 1 признаку , поэтому . Так как и
, то
и
Так как М – середина отрезка
ВС, поэтому
Аналогично,
, то
и
Так как М – середина отрезка
ВС, поэтому
Аналогично,
О
С
Д
N
М
В
А
Слайд 15Применение векторов к решению задач
Отсюда следует, что векторы
и коллинеарны, и,
значит точка О лежит на
прямой MN
О
С
Д
N
М
В
А