- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме : Векторы в пространстве
Содержание
- 1. Презентация по теме : Векторы в пространстве
- 2. А(-3; -2; 4) и В(-4; 3; 2) Найти модуль вектора АВ
- 3. А( 2; -3; 1), В( 4; -5;
- 4. Коллинеарны ли векторы AB и CD, если
- 5. Угол между векторами.
- 6. baOABαOA = a, OB = b( a
- 7. Скалярное произведение векторов.
- 8. Cкалярным произведением называется произведение длин этих векторов
- 9. Свойства скалярного произведения векторов.1) Скалярное произведение равно
- 10. Свойства скалярного произведения векторов.3) a * b
- 11. Скалярное произведение в координатах. Скалярным произведение векторов
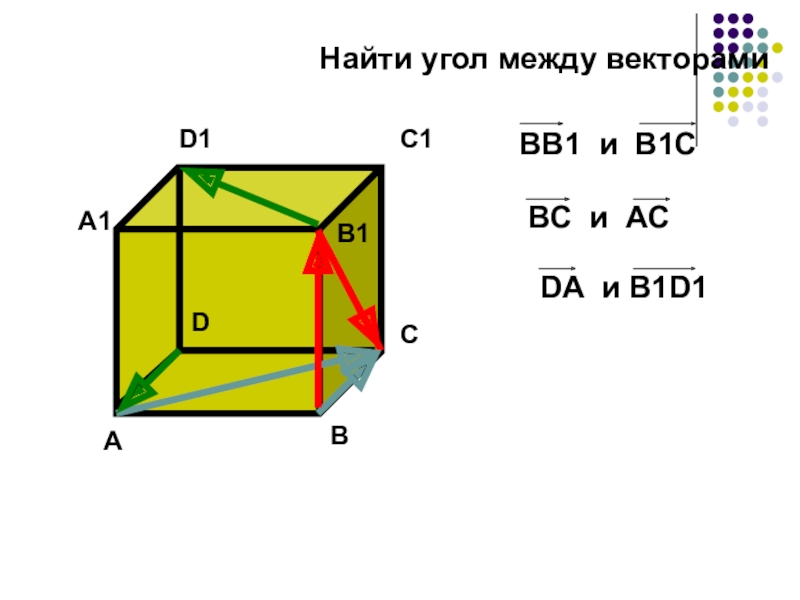
- 12. ADCBA1D1C1B1Найти угол между векторамиBB1 и B1CBC и ACDA и B1D1
- 13. Вычисли угол между вектором а {2; 1; 2} координатным векторомi
А(-3; -2; 4) и В(-4; 3; 2) Найти модуль вектора АВ
Слайд 6b
a
O
A
B
α
OA = a, OB = b
( a b ) = α
Если
векторы сонаправлены, то угол между
ними равен 0˚.
Если векторы противоположно напрвлены,
то угол между ними равен 180˚.
Если векторы перпендикулярны, то угол
между ними равен 90˚.
ними равен 0˚.
Если векторы противоположно напрвлены,
то угол между ними равен 180˚.
Если векторы перпендикулярны, то угол
между ними равен 90˚.
Слайд 8Cкалярным произведением называется
произведение длин этих векторов на косинус угла
между
данными векторами.
a * b = a * b * cos( a b )
cos ( a b) =
a * b = a * b * cos( a b )
cos ( a b) =
a * b
I a I * I b I
а * b - число (скаляр) от латинского лестница, шкала.
Впервые этот термин ввёл английский математик
У.Гамильтон в 1845г.
Слайд 9Свойства скалярного произведения векторов.
1) Скалярное произведение равно 0 тогда и только
тогда, когда векторы перпендикулярны.
2) Скалярный квадрат вектора равен квадрату его длины.
a*а = IaI*IaI*cos0˚; a² = IaI²
2) Скалярный квадрат вектора равен квадрату его длины.
a*а = IaI*IaI*cos0˚; a² = IaI²
Слайд 10Свойства скалярного произведения векторов.
3) a * b = b * a
(переместительный закон)
4) ( a + b)*c = a*c + b*c (сочетательный закон)
5) k*(a * b) = (k*a)*b
4) ( a + b)*c = a*c + b*c (сочетательный закон)
5) k*(a * b) = (k*a)*b
Слайд 11Скалярное произведение в координатах.
Скалярным произведение векторов называется сумма произведений соответствующих
координат этих векторов.
a {x;y;z}, b {m;n;f}
a * b = x*m + y*n + z*f
cos ( a b ) =
a {x;y;z}, b {m;n;f}
a * b = x*m + y*n + z*f
cos ( a b ) =
x*m + y*n + z*f
√x²+y²+z² * √m²+n²+f²