- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Теорема синусов
Содержание
- 1. Презентация по теме: Теорема синусов
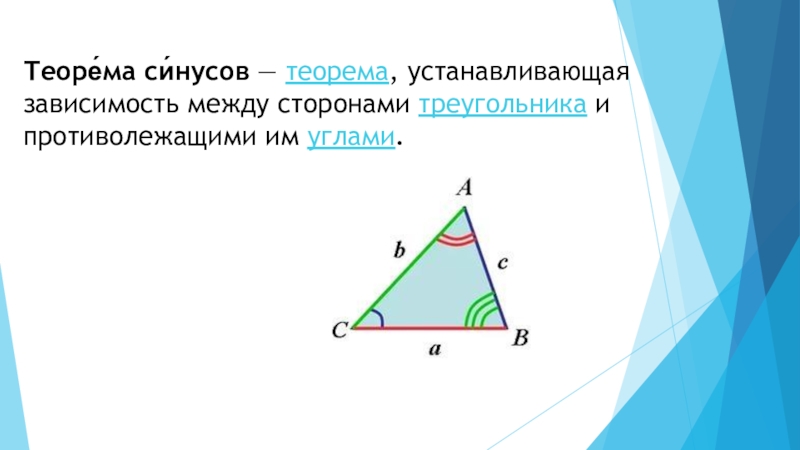
- 2. Теоре́ма си́нусов — теорема, устанавливающая зависимость между сторонами треугольника и противолежащими им углами.
- 3. Сформулируем, проанализируем и докажем теорему синусов.
- 4. Формулировка и доказательство следствия из теоремы синусовИз
- 5. 1. Угол– острый в треугольнике АВС.Проведём диаметрВ
- 6. 2. Угол– тупой в треугольнике АВС.Проведём диаметр
- 7. 3. Угол.В прямоугольнике АВС угол А прямой,
Слайд 2Теоре́ма си́нусов — теорема, устанавливающая зависимость между сторонами треугольника и противолежащими им углами.
Слайд 3Сформулируем, проанализируем и докажем теорему синусов.
стороны треугольника пропорциональны синусам противолежащих углов.
Формула для данной теоремы:
Докажем данную теорему с помощью формулы площади треугольника через синус его угла:
Из этой формулы мы получаем два соотношения:
1.
На b сокращаем, синусы помещаем в знаменатели:
2.
Из этих двух соотношений получаем:
Теорема доказана.
Слайд 4Формулировка и доказательство следствия из теоремы синусов
Из теоремы синусов вытекает важное
где R – радиус описанной около треугольника окружности.
Следовательно, мы получили три формулы радиуса описанной окружности:
Но, по существу, весь смысл следствия из теоремы синусов заключён в формуле:
Радиус описанной окружности не зависит от угла α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства рассмотрим три случая:
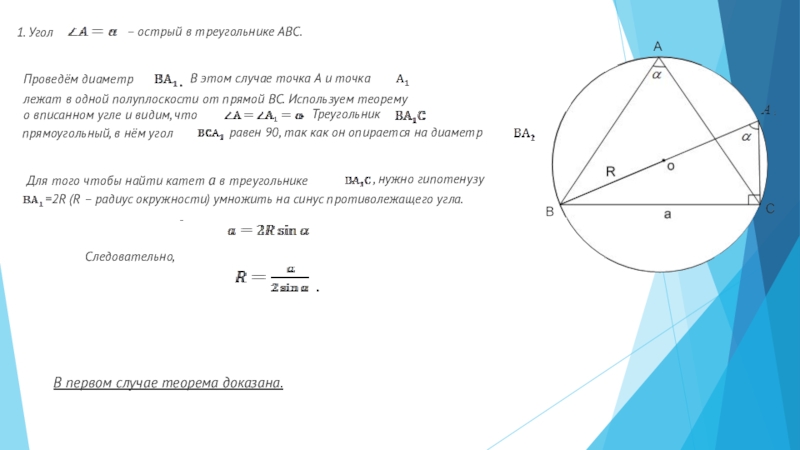
Слайд 51. Угол
– острый в треугольнике АВС.
Проведём диаметр
В этом случае точка А
.
лежат в одной полуплоскости от прямой ВС. Используем теорему
о вписанном угле и видим, что
.
Треугольник
прямоугольный, в нём угол
равен 90, так как он опирается на диаметр
.
Для того чтобы найти катет a в треугольнике
, нужно гипотенузу
=2R (R – радиус окружности) умножить на синус противолежащего угла.
Следовательно,
.
В первом случае теорема доказана.
Слайд 62. Угол
– тупой в треугольнике АВС.
Проведём диаметр окружности
.
Точки А и
по разные
от прямой ВС. Четырёхугольник
вписан в окружность, и его свойство
таково, что сумма противолежащих углов равна
.
Следовательно,
=
.
Вспомним данное свойство вписанного в окружность четырёхугольника:
Также мы знаем, что
.
В треугольнике
угол при вершине С равен 90 , потому что он опирается на
диаметр. Следовательно, катет а мы находим таким образом:
Следовательно,
Во втором случае теорема доказана.
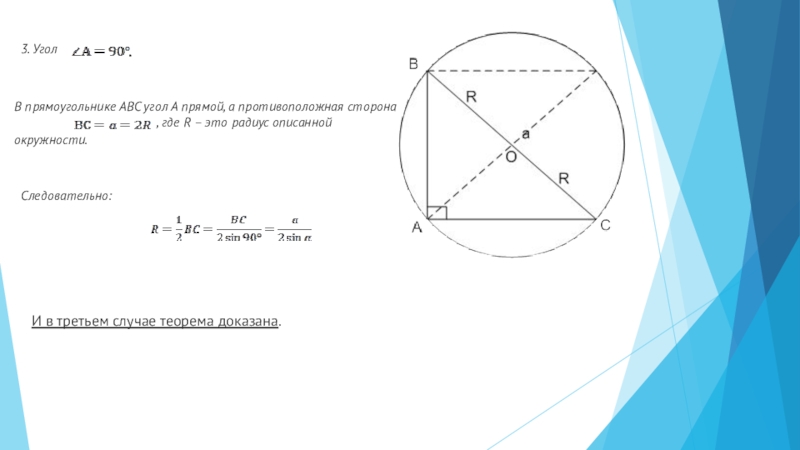
Слайд 73. Угол
.
В прямоугольнике АВС угол А прямой, а противоположная сторона
, где
окружности.
Следовательно:
И в третьем случае теорема доказана.