- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Теорема Пифагора
Содержание
- 1. Презентация по теме Теорема Пифагора
- 2. ПифагорРодился на о. Самос в Эгейском море
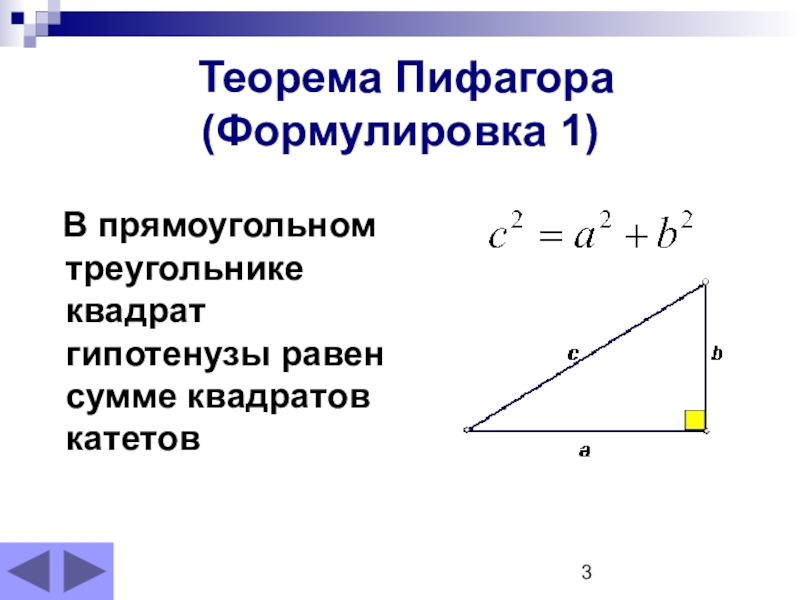
- 3. Теорема Пифагора (Формулировка 1) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
- 4. О треугольнике со сторонами 3,
- 5. Слайд 5
- 6. ДоказательствоДано: прямоугольный треугольник с катетами а, b
- 7. Теорема Пифагора (Формулировка 2) Площадь
- 8. Теорема не теряет смысла, если квадраты заменить любыми другими правильными многоугольниками или полукругами.
- 9. Если на сторонах треугольника построены полукруги
- 10. ДоказательствоСумма площади полукругов, построенных на катетах, равна
- 11. Доказательство Бхаскары Из всего текста имеется только формула:
- 12. Рисунок иллюстрирует доказательство теоремы Пифагора, придуманное Леонардо да Винчи. Доказательство Леонардо да Винчи
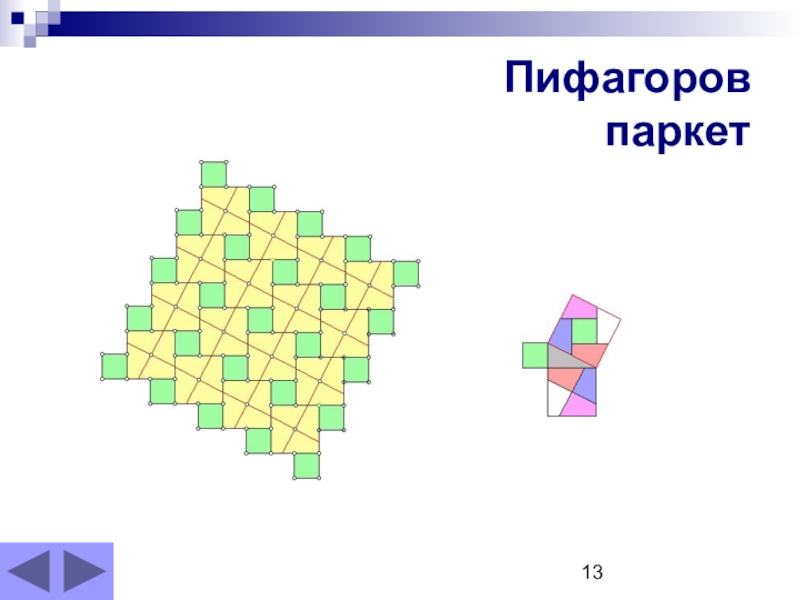
- 13. Слайд 13
- 14. Теорема Пифагора по ЕвклидуШаг 1.
- 15. Теорема Пифагора по ЕвклидуШаг 2.
- 16. Теорема Пифагора по ЕвклидуШаг 3.
- 17. Теорема Пифагора по ЕвклидуШаг 4.При всех преобразованиях
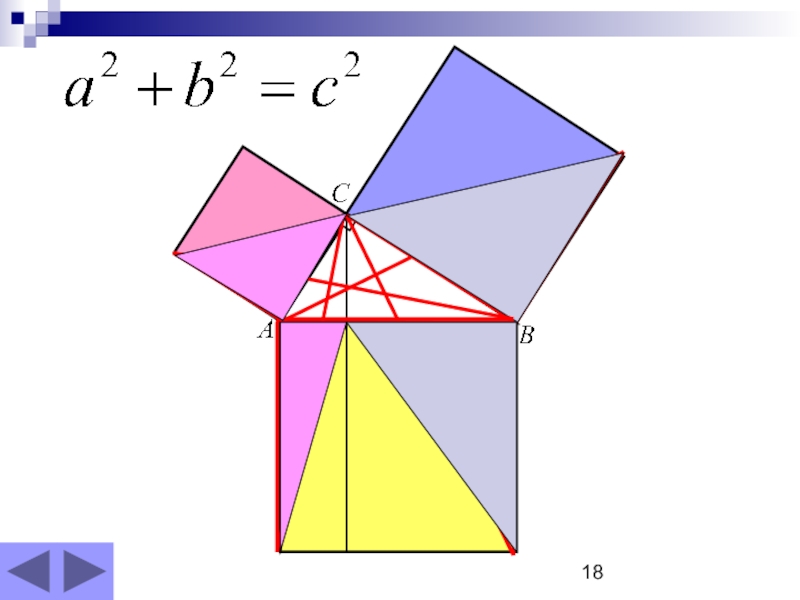
- 18. Слайд 18
- 19. Прямоугольные треугольники, длины сторон которых – целые
- 20. К теореме Пифагора его ученики составляли
- 21. Теорему называли «мостом ослов», так как слабые
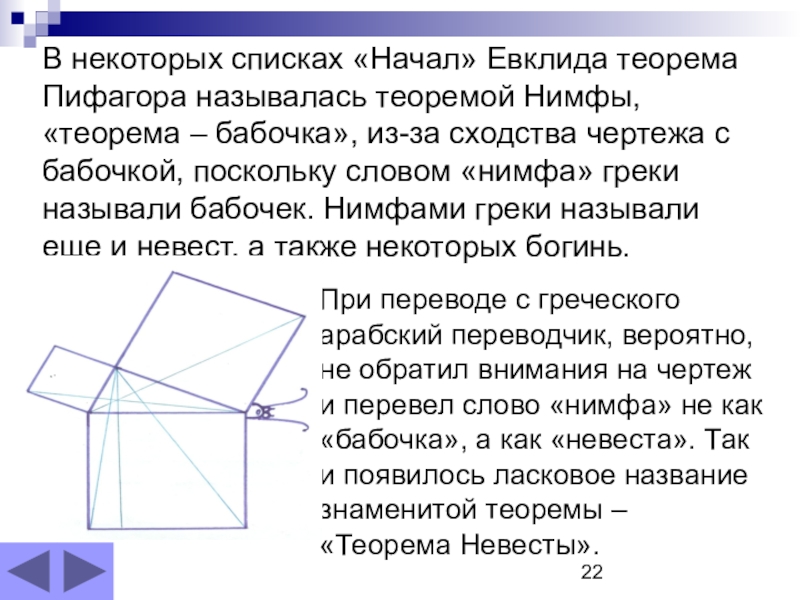
- 22. В некоторых списках «Начал» Евклида теорема Пифагора
- 23. Задачи
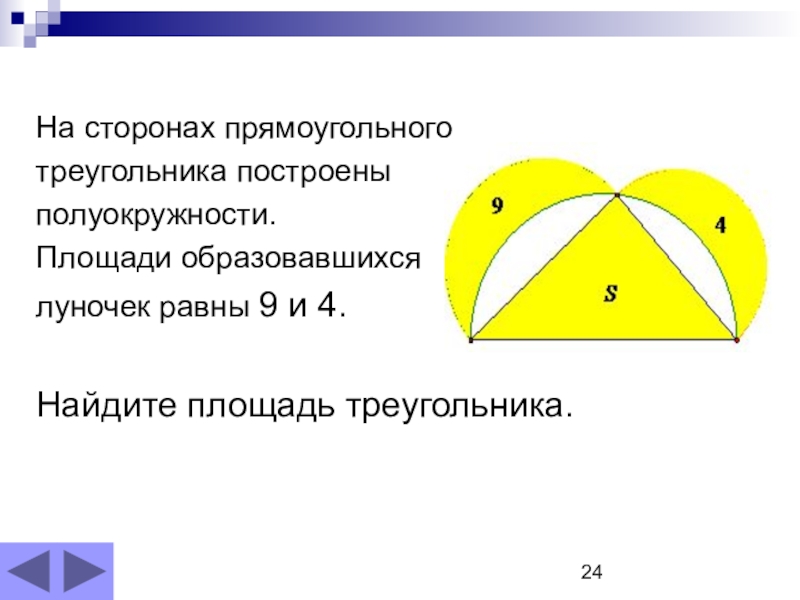
- 24. На сторонах прямоугольного треугольника построены полуокружности. Площади образовавшихся луночек равны 9 и 4.Найдите площадь треугольника.
- 25. Решение задачиДано:
- 26. Имеется бамбук высотой в
- 27. РешениеДано: АВС – прямоугольный треугольник;
- 28. Обратная теореме Пифагора
- 29. Обратная теореме ПифагораЗемлемеры и строители Древнего Египта
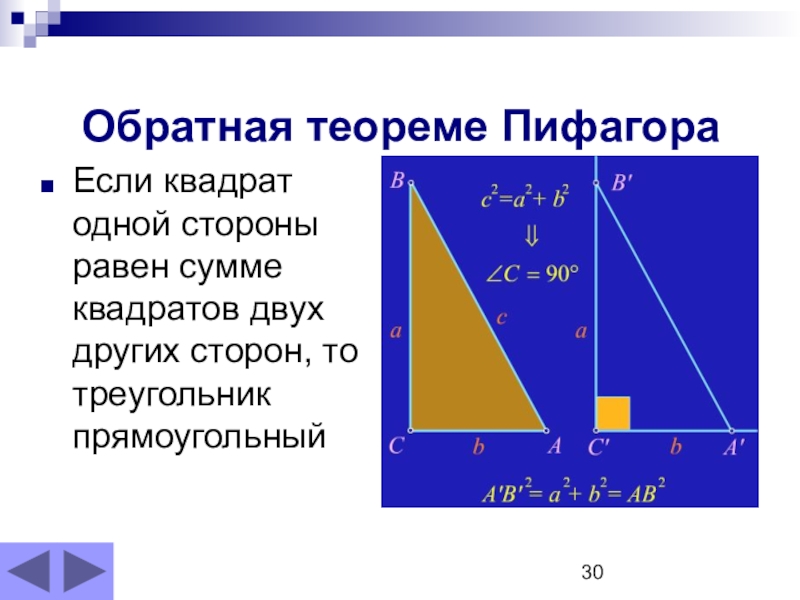
- 30. Обратная теореме Пифагора Если квадрат одной стороны
- 31. Слайд 31
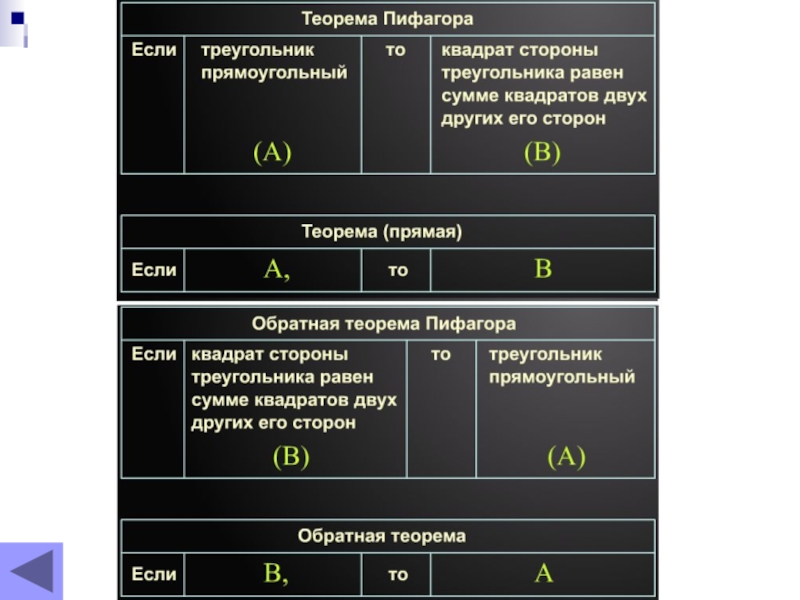
- 32. ЗаданиеСравните таблицы «Теорема Пифагора» и «Обратная теореме Пифагора».
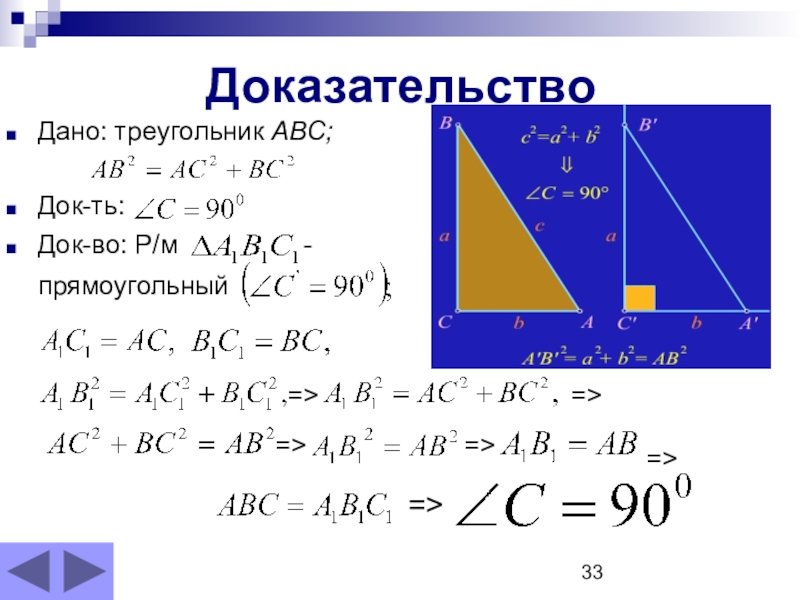
- 33. ДоказательствоДано: треугольник ABC;
- 34. Слайд 34
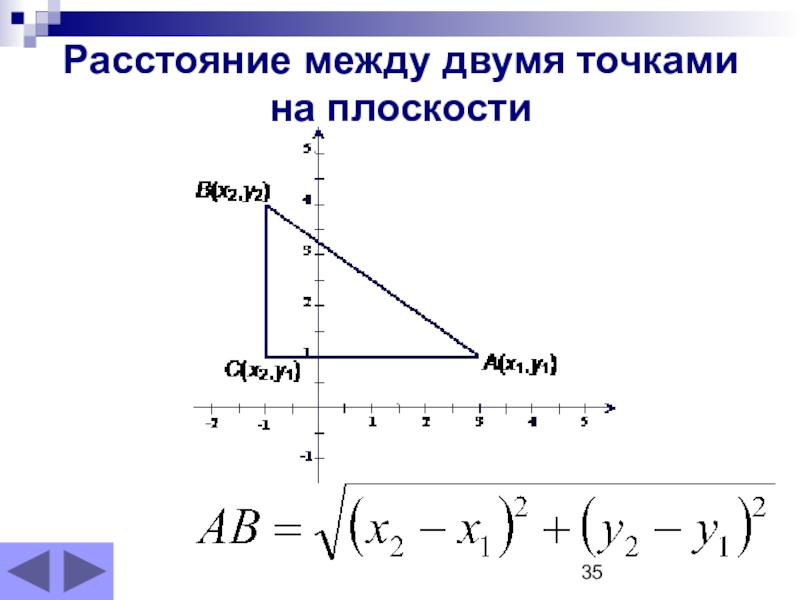
- 35. Расстояние между двумя точками на плоскости
- 36. Теорема Пифагора в пространствеКвадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений.
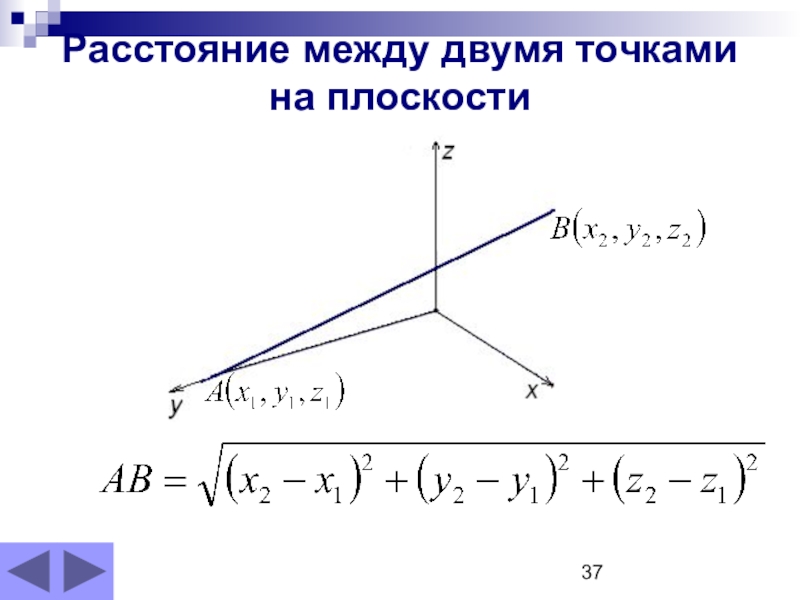
- 37. Расстояние между двумя точками на плоскости
- 38. Теорема Пифагора и физика
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
ПифагорРодился на о. Самос в Эгейском море Во время путешествия в возрасте 18–20 лет посетил математика Фалеса В южноиталийском г. Кротоне основал пифагорейский союз (школу)В школе считали, что в основе всего лежат числа и гармония, но
Слайд 2Пифагор
Родился на о. Самос в Эгейском море
Во время путешествия в
возрасте 18–20 лет посетил математика Фалеса
В южноиталийском г. Кротоне основал пифагорейский союз (школу)
В школе считали, что в основе всего лежат числа и гармония, но все в математике нужно доказывать
После 30-летнего существования союза Пифагор с учениками уехал в г. Тарент, а потом в г. Месапонт, где и погиб от рук солдата почти 95-летний Пифагор
В южноиталийском г. Кротоне основал пифагорейский союз (школу)
В школе считали, что в основе всего лежат числа и гармония, но все в математике нужно доказывать
После 30-летнего существования союза Пифагор с учениками уехал в г. Тарент, а потом в г. Месапонт, где и погиб от рук солдата почти 95-летний Пифагор
Слайд 3 Теорема Пифагора
(Формулировка 1)
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов
Слайд 4О треугольнике со сторонами 3, 4, 5 (
)– говорится в папирусе (2000 г. до н. э.). Соотношение между сторонами прямоугольного треугольника обнаружили и на вавилонских клинописных табличках, и в древнекитайских и древнеиндийских трактатах.
Слайд 6Доказательство
Дано: прямоугольный треугольник с катетами а, b и гипотенузой с
Док-ть:
Док-во:
достроим треугольник до квадрата со стороной a+b
S= =
S= =
= =
=>
S= =
S= =
= =
=>
Слайд 7Теорема Пифагора
(Формулировка 2)
Площадь квадрата, построенного на гипотенузе,
равна сумме площадей квадратов, построенных на катетах.
Слайд 8Теорема не теряет смысла, если квадраты заменить любыми другими правильными многоугольниками
или полукругами.
Слайд 9 Если на сторонах треугольника построены полукруги по одну сторону гипотенузы,
то площадь полученных луночек равна площади данного треугольника.
Слайд 10Доказательство
Сумма площади полукругов, построенных на катетах, равна площади полукруга, построенного на
гипотенузе, и из них вычитаются одни и те же сектора (выделенные оранжевым цветом)
Слайд 12
Рисунок иллюстрирует доказательство теоремы Пифагора, придуманное Леонардо да Винчи.
Доказательство Леонардо
да Винчи
Слайд 17Теорема Пифагора по Евклиду
Шаг 4.
При всех преобразованиях треугольника его площадь не
меняется.
Аналогично и для другого катета.
Аналогично и для другого катета.
Слайд 19Прямоугольные треугольники, длины сторон которых – целые числа, называются Пифагоровыми
Прямоугольный
треугольник со сторонами 3, 4, 5 называется Египетским
тройки (a, b, c) натуральных чисел, удовлетворяющие уравнению - Пифагоровыми
тройки (a, b, c) натуральных чисел, удовлетворяющие уравнению - Пифагоровыми
Слайд 20 К теореме Пифагора его ученики составляли стишки:
«Пифагоровы штаны
во все стороны
равны»,
А также рисовали карикатуры:
Шарж из учебника XVI века.
Слайд 21Теорему называли «мостом ослов», так как слабые ученики, заучивающие теоремы наизусть,
без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.
Или «бегство убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии.
Или «бегство убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии.
"Dons asinorum"
"elefuga"
Слайд 22В некоторых списках «Начал» Евклида теорема Пифагора называлась теоремой Нимфы, «теорема
– бабочка», из-за сходства чертежа с бабочкой, поскольку словом «нимфа» греки называли бабочек. Нимфами греки называли еще и невест, а также некоторых богинь.
При переводе с греческого арабский переводчик, вероятно, не обратил внимания на чертеж и перевел слово «нимфа» не как «бабочка», а как «невеста». Так и появилось ласковое название знаменитой теоремы – «Теорема Невесты».
Слайд 24На сторонах прямоугольного
треугольника построены
полуокружности.
Площади образовавшихся
луночек равны 9
и 4.
Найдите площадь треугольника.
Найдите площадь треугольника.
Слайд 26
Имеется бамбук высотой в 1 чжан. Вершину его согнули
так, что она касается земли на расстоянии 3 чи от корня (1 чжан = 10 чи).
Какова высота бамбука после сгибания?
Слайд 27Решение
Дано: АВС – прямоугольный треугольник;
АС+АВ=10 чи;
ВС=3 чи.
Найти: АС=?
Решение: (по Т. Пифагора)=>
пусть АС=х чи,
тогда АВ=10-х (АВ=10-АС), ВС=3 чи.
(чи)
Ответ: Высота бамбука после
сгибания равна 4,55 чи.
Найти: АС=?
Решение: (по Т. Пифагора)=>
пусть АС=х чи,
тогда АВ=10-х (АВ=10-АС), ВС=3 чи.
(чи)
Ответ: Высота бамбука после
сгибания равна 4,55 чи.
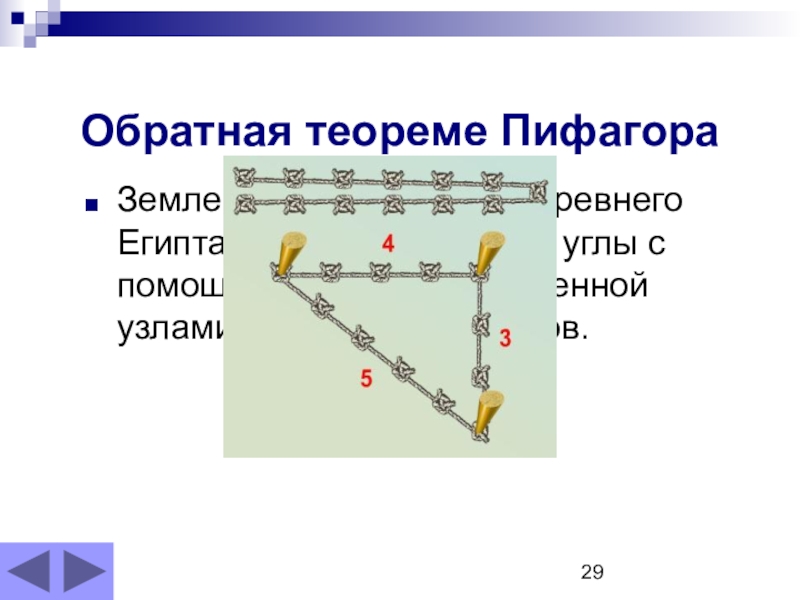
Слайд 29Обратная теореме Пифагора
Землемеры и строители Древнего Египта размечали прямые углы с
помощью веревки, разделенной узлами на 12 равных кусков.
Посмотри!
Посмотри!
Слайд 30Обратная теореме Пифагора
Если квадрат одной стороны равен сумме квадратов двух
других сторон, то треугольник прямоугольный
Слайд 36Теорема Пифагора в пространстве
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его
измерений.
