не усвоил ничего нового, ничего не прибавил к своему образованию»
Ян Амос Каменский
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Двугранный угол
Содержание
- 1. Презентация по теме Двугранный угол
- 2. Эпиграф урока:«Считай несчастным тот день или тот
- 3. Кроссворд1)Отрезок, соединяющий точку, не лежащую на данной
- 4. Теоретическая
- 5. 2) Признак перпендикулярности прямой и плоскости.Если прямая
- 6. 3) Что называется перпендикуляром, опущенным из данной
- 7. 4) Что называется наклонной, проведённой из данной
- 8. 5) Что называется углом между прямой и
- 9. 6) Что называется расстоянием от точки до
- 10. 7) Что называется расстоянием от точки до
- 11. 8) Какие прямые называются скрещивающимися?Две прямые называются
- 12. Слайд 12
- 13. 9) Что называется двугранным углом?Двугранным углом называется
- 14. 10) Что называется линейным углом двугранного угла?Линейным
- 15. 11) Свойство пирамиды с равными боковыми рёбрамиЕсли
- 16. Свойство пирамиды с равнонаклонёнными к основанию
- 17. 12) Свойство пирамиды с равными высотами боковых
- 18. Свойство пирамиды с равнонаклонёнными к основанию
- 19. АНП-РМ Теорема о трех перпендикулярах.
- 20. АНП-РМОбратная
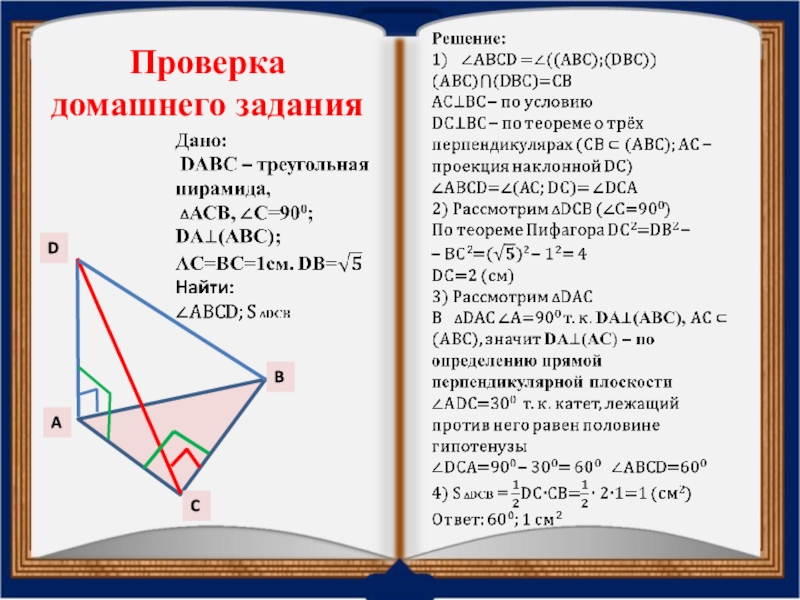
- 21. Проверка домашнего задания
- 22. Слайд 22
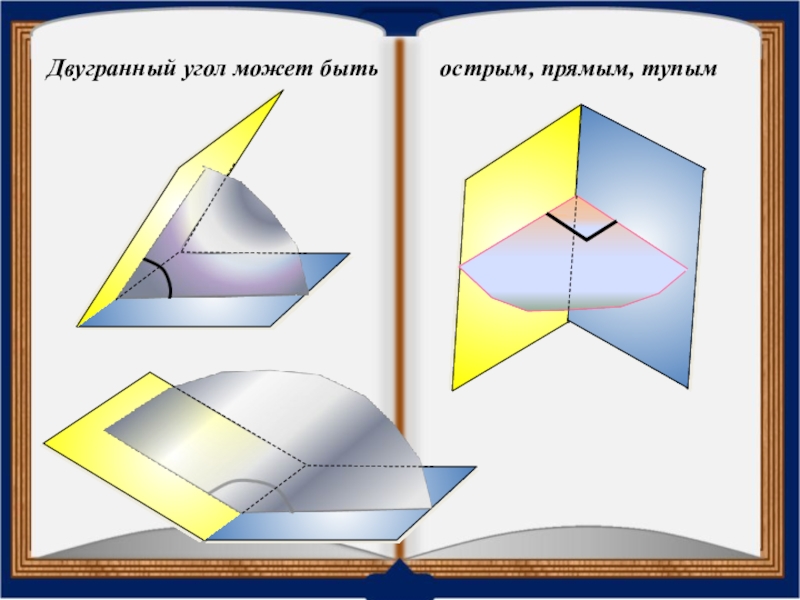
- 23. Двугранный угол может быть острым, прямым, тупым
- 24. ВСMЗадача 1Из точки В к плоскости проведена
- 25. Задача 2 В ∆АВС ∠ С
- 26. Задача 3: В кубе A…D1 найдите угол между плоскостями ABC и CDD1.Ответ: 90o.
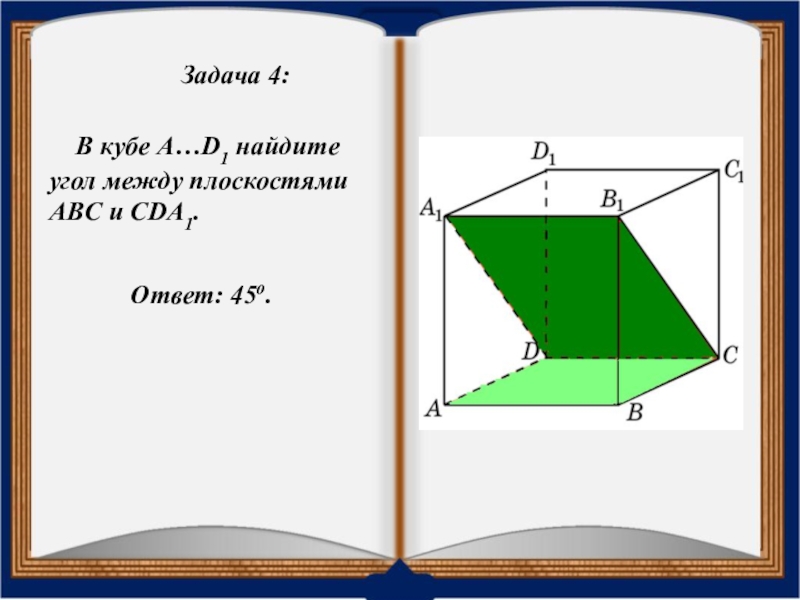
- 27. Задача 4: В кубе A…D1 найдите угол между плоскостями ABC и CDA1.Ответ: 45o.
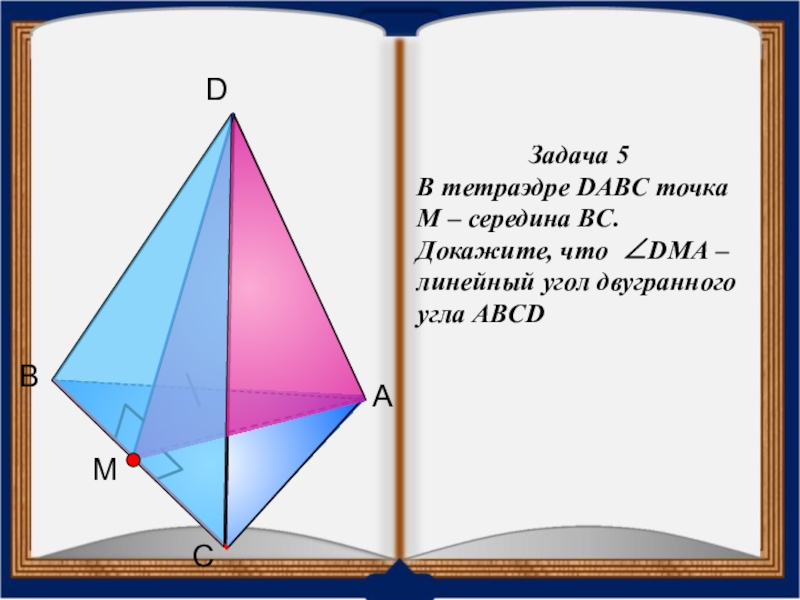
- 28. Задача 5В тетраэдре DABC точка М –
- 29. Задача В правильной треугольной пирамидеSABC сторона основания
- 30. Физкультминутка
- 31. Самостоятельная работа Построение линейных углов
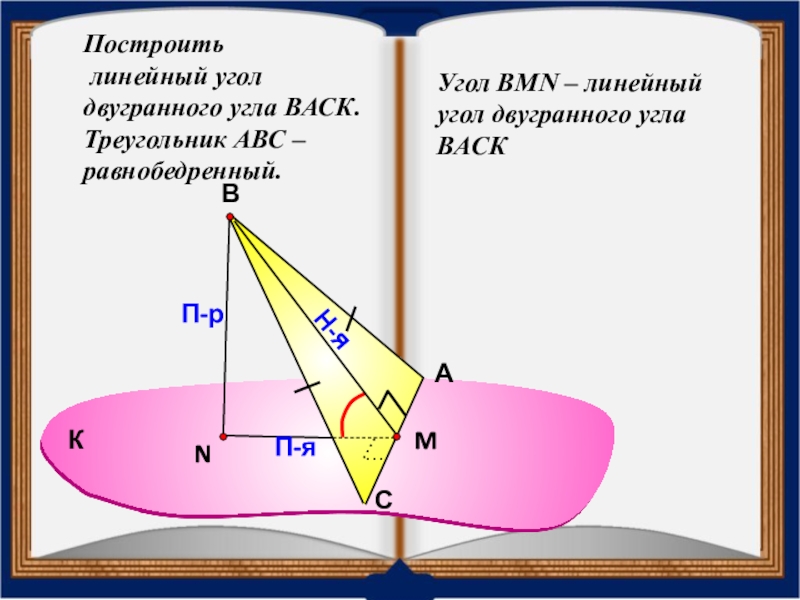
- 32. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – равнобедренный.АСВП-рН-яП-яУгол ВMN – линейный угол двугранного угла ВАСКК
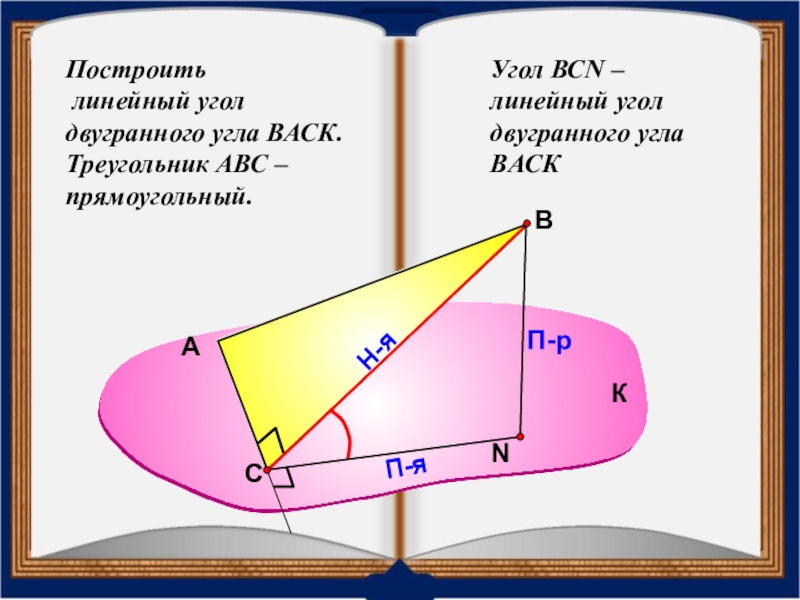
- 33. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – прямоугольный.АВП-рН-яП-яУгол ВСN – линейный угол двугранного угла ВАСККС
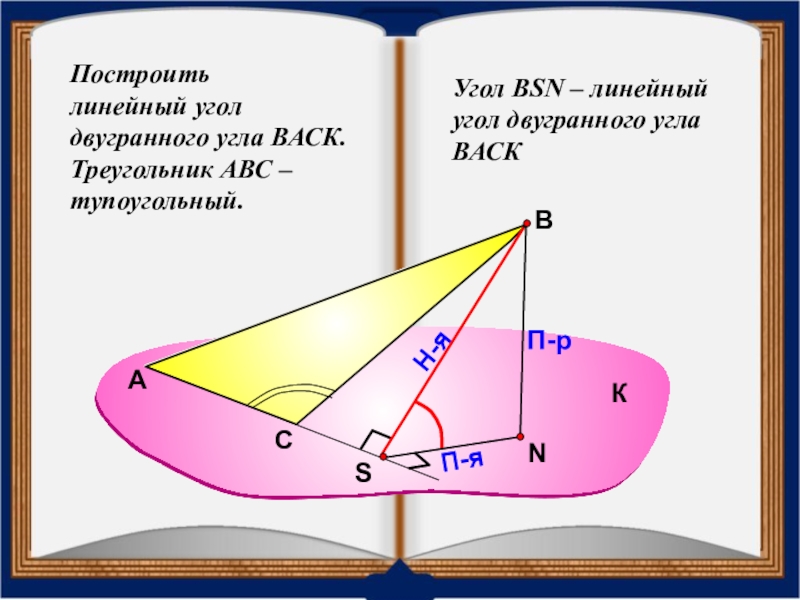
- 34. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – тупоугольный.АВП-рН-яП-яУгол ВSN – линейный угол двугранного угла ВАСККС
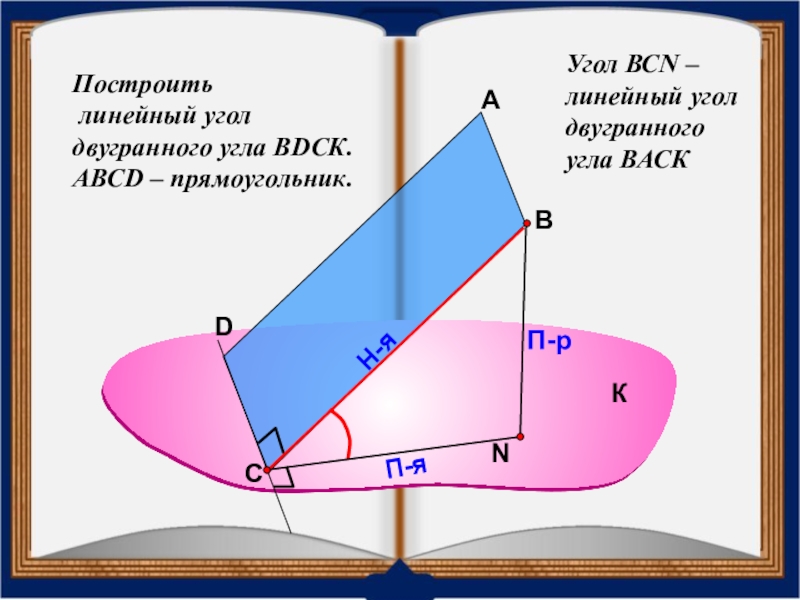
- 35. Построить линейный угол двугранного угла ВDСК.АВСD – прямоугольник.АВП-рН-яП-яУгол ВСN – линейный угол двугранного угла ВАСККСD
- 36. Построить линейный угол двугранного угла ВDСК.АВСD –
- 37. Построить линейный угол двугранного угла ВDСК.АВСD –
- 38. Построить линейный угол двугранного угла ВDСК.АВСD –
- 39. Домашнее задание№ 421, 423 ( учебник)
- 40. К математике способность проявляй, Не ленись, а
Эпиграф урока:«Считай несчастным тот день или тот час, в котором, ты не усвоил ничего нового, ничего не прибавил к своему образованию»Ян Амос Каменский
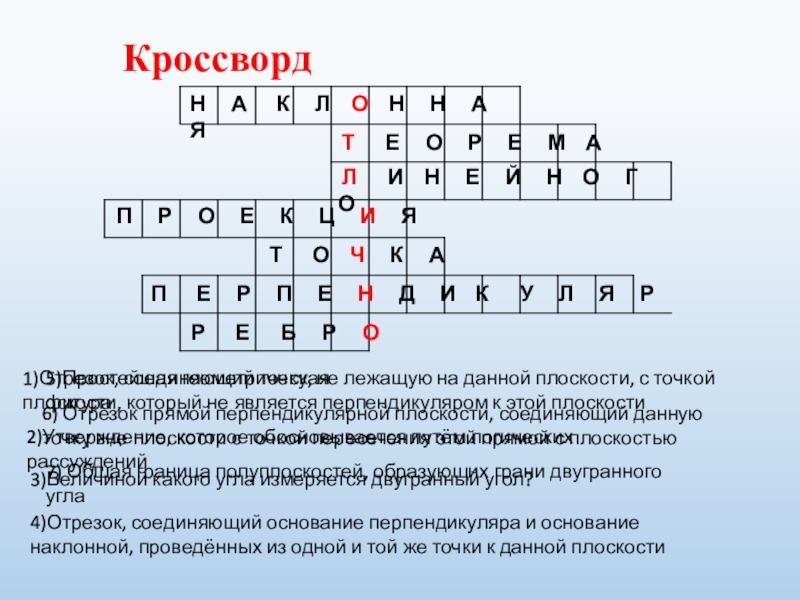
Слайд 3Кроссворд
1)Отрезок, соединяющий точку, не лежащую на данной плоскости, с точкой плоскости,
который не является перпендикуляром к этой плоскости
Н А К Л О Н Н А Я
Т Е О Р Е М А
2)Утверждение, которое обосновывается путём логических рассуждений
3)Величиной какого угла измеряется двугранный угол?
Л И Н Е Й Н О Г О
4)Отрезок, соединяющий основание перпендикуляра и основание наклонной, проведённых из одной и той же точки к данной плоскости
П Р О Е К Ц И Я
5)Простейшая геометрическая фигура
Т О Ч К А
6) Отрезок прямой перпендикулярной плоскости, соединяющий данную точку вне плоскости с точкой пересечения этой прямой с плоскостью
П Е Р П Е Н Д И К У Л Я Р
7) Общая граница полуплоскостей, образующих грани двугранного угла
Р Е Б Р О
Слайд 4Теоретическая разминка
1) Определение
прямой, перпендикулярной плоскости.
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в плоскости.
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в плоскости.
Слайд 52) Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна двум пересекающимся прямым,
лежащим в плоскости, то она перпендикулярна плоскости
Слайд 63) Что называется перпендикуляром, опущенным из данной точки на данную плоскость.
Что называется основанием этого перпендикуляра?
Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок прямой, перпендикулярной плоскости, соединяющий данную точку вне плоскости с точкой пересечения этой прямой с плоскостью. Основанием перпендикуляра называется конец отрезка, лежащий в плоскости.
Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок прямой, перпендикулярной плоскости, соединяющий данную точку вне плоскости с точкой пересечения этой прямой с плоскостью. Основанием перпендикуляра называется конец отрезка, лежащий в плоскости.
Слайд 74) Что называется наклонной, проведённой из данной точки к данной плоскости?
Что называется основанием наклонной?
Наклонной, проведённой из данной точки к данной плоскости, называется любой отрезок, соединяющий эту точку с точкой плоскости, который не является перпендикуляром к плоскости. Основанием наклонной называется конец этого отрезка, лежащий в плоскости.
Наклонной, проведённой из данной точки к данной плоскости, называется любой отрезок, соединяющий эту точку с точкой плоскости, который не является перпендикуляром к плоскости. Основанием наклонной называется конец этого отрезка, лежащий в плоскости.
Слайд 85) Что называется углом между прямой и плоскостью?
Углом между прямой и
плоскостью называется угол между прямой и её проекцией на эту плоскость (если прямая параллельна плоскости, то этот угол равен 00, если перпендикулярна – 900)
Слайд 96) Что называется расстоянием от точки до прямой?
Расстоянием от точки до
прямой называется длина перпендикуляра, опущенного из данной точки на данную прямую
Слайд 107) Что называется расстоянием от точки до плоскости?
Расстоянием от точки до
плоскости называется длина перпендикуляра, опущенного из данной точки на данную плоскость
Слайд 118) Какие прямые называются скрещивающимися?
Две прямые называются скрещивающимися, если они не
лежат в одной плоскости, т.е. не параллельны и не пересекаются
Слайд 139) Что называется двугранным углом?
Двугранным углом называется угол, образованный двумя полуплоскостями
с общей границей. Полуплоскости – это грани угла, общая граница – это ребро двугранного угла. Измеряется величиной своего линейного угла.
Слайд 1410) Что называется линейным углом двугранного угла?
Линейным углом двугранного угла называется
угол, образованный двумя лучами, выходящими из любой точки на ребре двугранного угла, проведёнными в каждой из граней перпендикулярно его ребру. Величина этого угла измеряется от 00 до 1800
Слайд 1511) Свойство пирамиды с равными боковыми рёбрами
Если боковые рёбра пирамиды равны,
то около основания пирамиды можно описать окружность и основание высоты пирамиды совпадает с центром этой окружности.
Слайд 16 Свойство пирамиды с равнонаклонёнными к основанию боковыми рёбрами
Если боковые рёбра
пирамиды равнонаклонены к основанию, то около основания пирамиды можно описать окружность и основание высоты пирамиды совпадает с центром этой окружности.
Слайд 1712) Свойство пирамиды с равными высотами боковых граней
Если высоты боковых граней
пирамиды равны, то около в основание пирамиды можно вписать окружность и основание высоты пирамиды совпадает с центром этой окружности.
Слайд 18 Свойство пирамиды с равнонаклонёнными к основанию боковыми гранями
Если боковые грани
пирамиды равнонаклонены к основанию, то в основание пирамиды можно вписать окружность и основание высоты пирамиды совпадает с центром этой окружности.
вписать
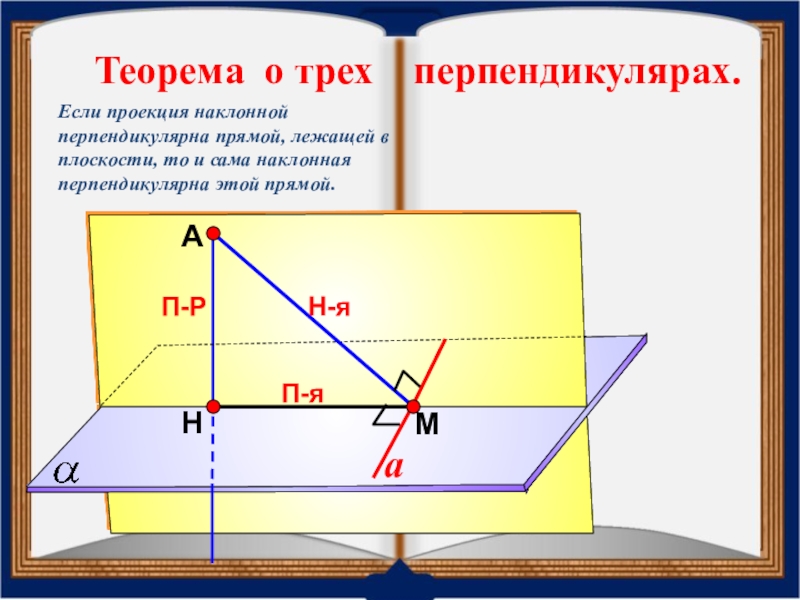
Слайд 19А
Н
П-Р
М
Теорема о трех перпендикулярах.
Н-я
Если проекция наклонной перпендикулярна
прямой, лежащей в плоскости, то и сама наклонная перпендикулярна этой прямой.
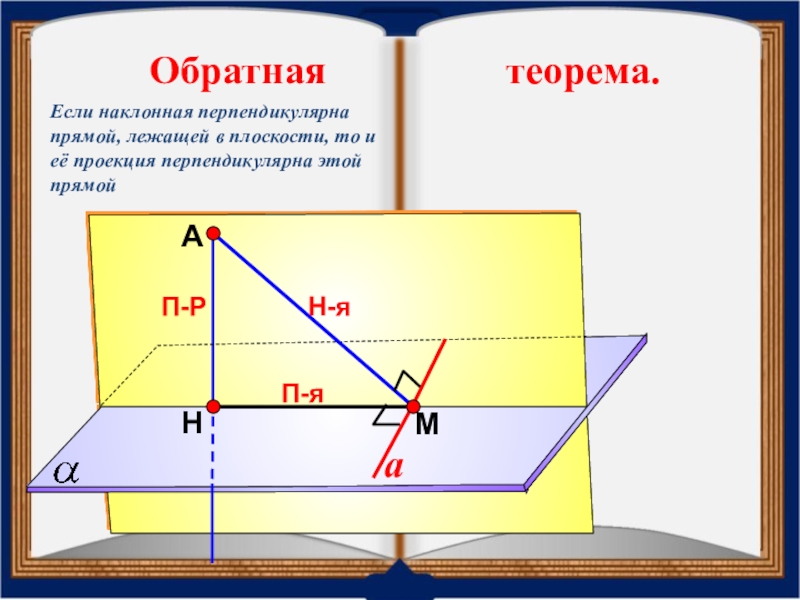
Слайд 20А
Н
П-Р
М
Обратная теорема.
Н-я
Если наклонная
перпендикулярна прямой, лежащей в плоскости, то и её проекция перпендикулярна этой прямой
Слайд 24В
С
M
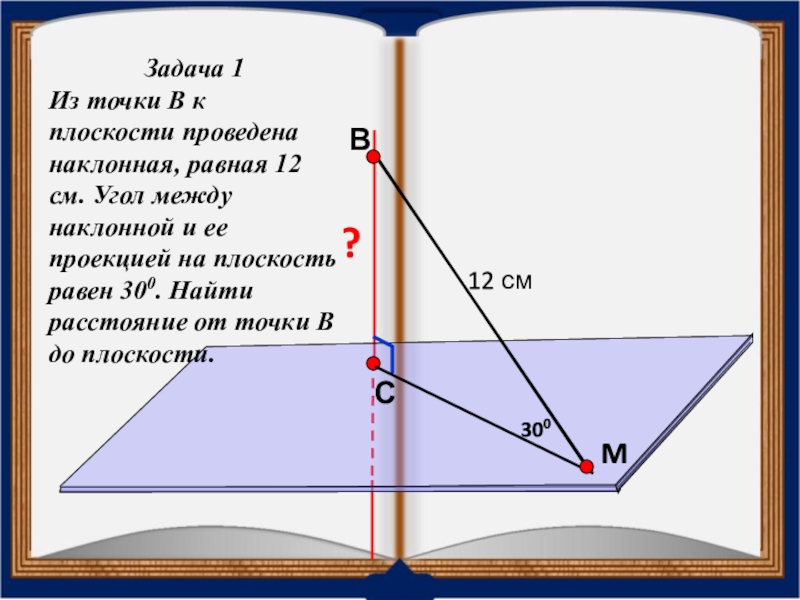
Задача 1
Из точки В к плоскости проведена наклонная, равная 12 см.
Угол между наклонной и ее проекцией на плоскость равен 300. Найти расстояние от точки В до плоскости.
12 см
300
?
Слайд 25
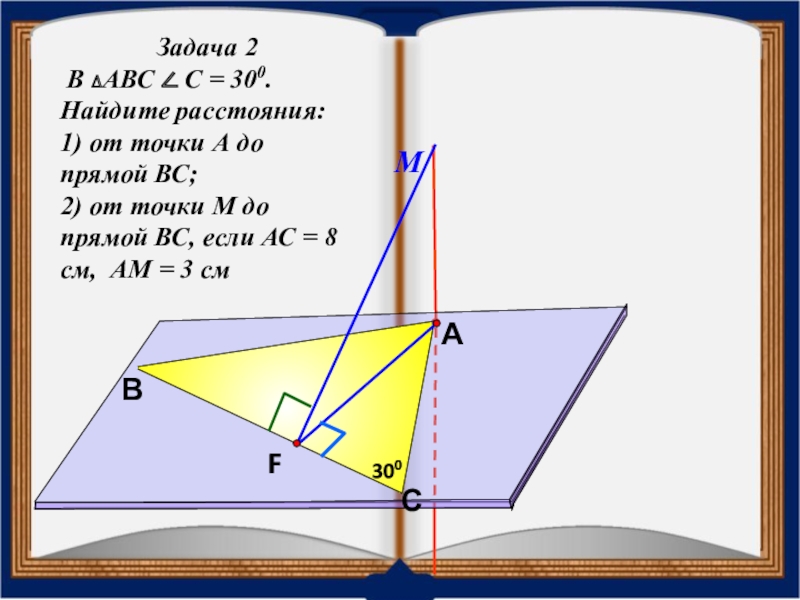
Задача 2
В ∆АВС ∠ С = 300. Найдите расстояния:
1) от точки А до прямой ВС;
2) от точки М до прямой ВС, если АС = 8 см, АМ = 3 см
2) от точки М до прямой ВС, если АС = 8 см, АМ = 3 см
А
В
С
300
Слайд 28Задача 5
В тетраэдре DABC точка М – середина BС.
Докажите, что ∠DMА
– линейный угол двугранного угла АBCD
Слайд 29Задача
В правильной треугольной пирамиде
SABC сторона основания равна 12 см, а
угол наклона боковой грани к плоскости
основания равен 60 Найдите высоту пирамиды
основания равен 60 Найдите высоту пирамиды
Слайд 32Построить
линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
А
С
В
П-р
Н-я
П-я
Угол ВMN –
линейный угол двугранного угла ВАСК
К
Слайд 33Построить
линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
А
В
П-р
Н-я
П-я
Угол ВСN –
линейный угол двугранного угла ВАСК
К
С
Слайд 34Построить
линейный угол
двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
А
В
П-р
Н-я
П-я
Угол ВSN –
линейный угол двугранного угла ВАСК
К
С
Слайд 35Построить
линейный угол
двугранного угла ВDСК.
АВСD – прямоугольник.
А
В
П-р
Н-я
П-я
Угол ВСN – линейный
угол двугранного угла ВАСК
К
С
D
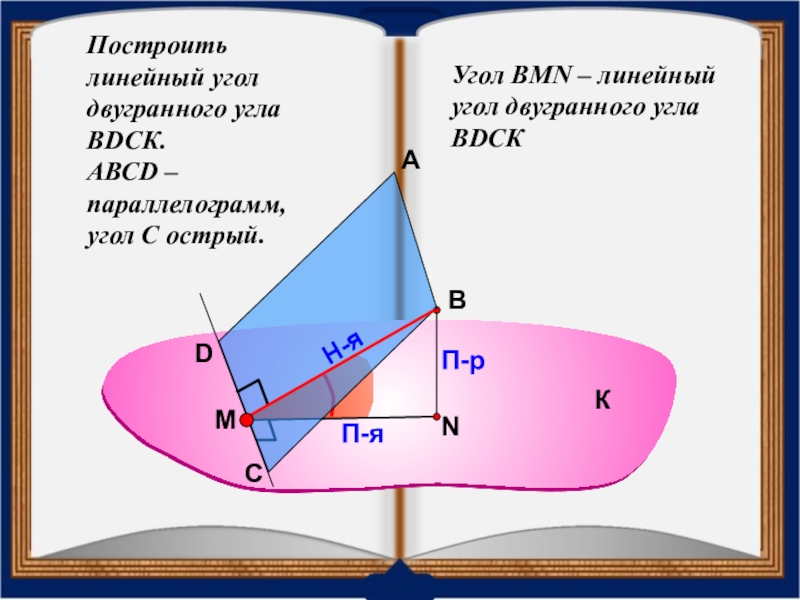
Слайд 36Построить
линейный угол двугранного угла ВDСК.
АВСD – параллелограмм,
угол С острый.
А
В
П-р
П-я
Угол
ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
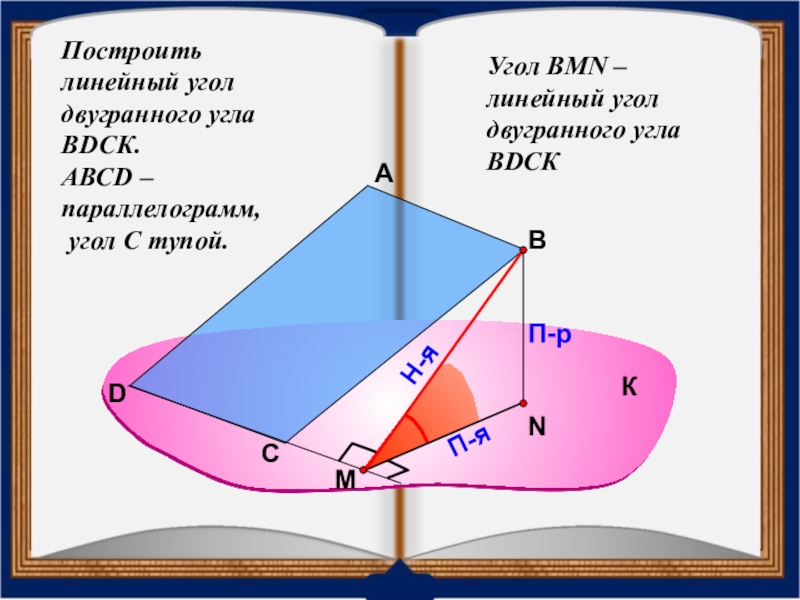
Слайд 37Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм,
угол С тупой.
А
В
П-р
П-я
Угол
ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
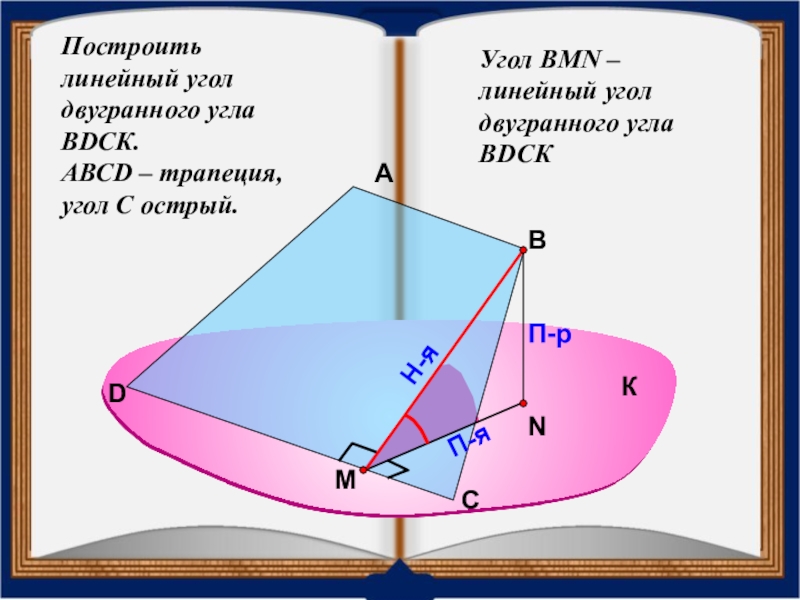
Слайд 38Построить
линейный угол
двугранного угла ВDСК.
АВСD – трапеция,
угол С острый.
А
В
П-р
П-я
Угол
ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
Слайд 40К математике способность проявляй,
Не ленись, а ежедневно развивай,
Повторяй, учи, трудись,
соображай,
С математикой дружить не забывай!
С математикой дружить не забывай!
Спасибо за работу.
До новых встреч!
