- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Аксиомы стереометрии
Содержание
- 1. Презентация по теме: Аксиомы стереометрии
- 2. Основные фигуры стереометрии и их обозначение.Основными фигурами
- 3. Первая аксиома стереометрии.Какова бы ни была плоскость,
- 4. Вторая аксиома стереометрии.Если две различные плоскости имеют
- 5. Третья аксиома стереометрии. Если две различны прямые
- 6. Решение задач.Задача 1.Точки A,B,C,D не лежат в
- 7. Задача 2.Точки A, B, C лежат в
- 8. Задача 3.Докажите, что точки A и B
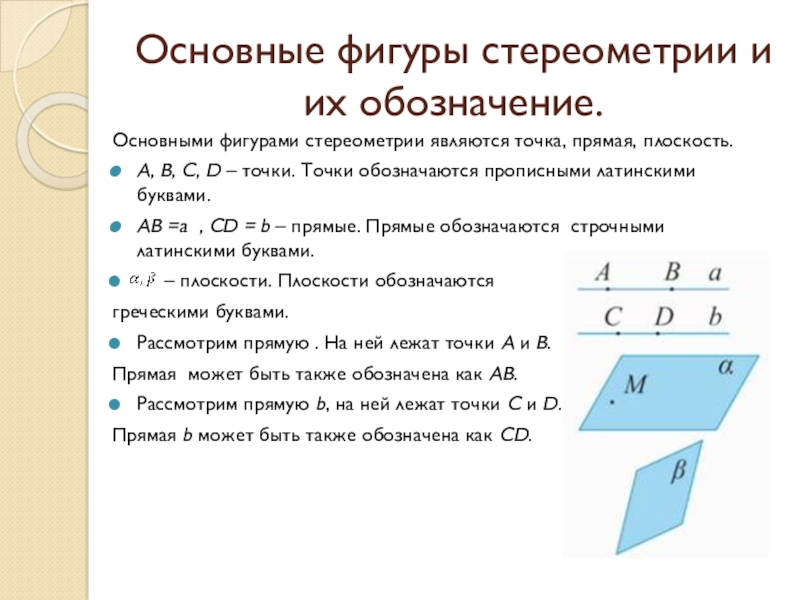
Слайд 2Основные фигуры стереометрии и их обозначение.
Основными фигурами стереометрии являются точка, прямая,
A, В, С, D – точки. Точки обозначаются прописными латинскими буквами.
АВ =a , CD = b – прямые. Прямые обозначаются строчными латинскими буквами.
– плоскости. Плоскости обозначаются
греческими буквами.
Рассмотрим прямую . На ней лежат точки А и В.
Прямая может быть также обозначена как АВ.
Рассмотрим прямую b, на ней лежат точки С и D.
Прямая b может быть также обозначена как СD.
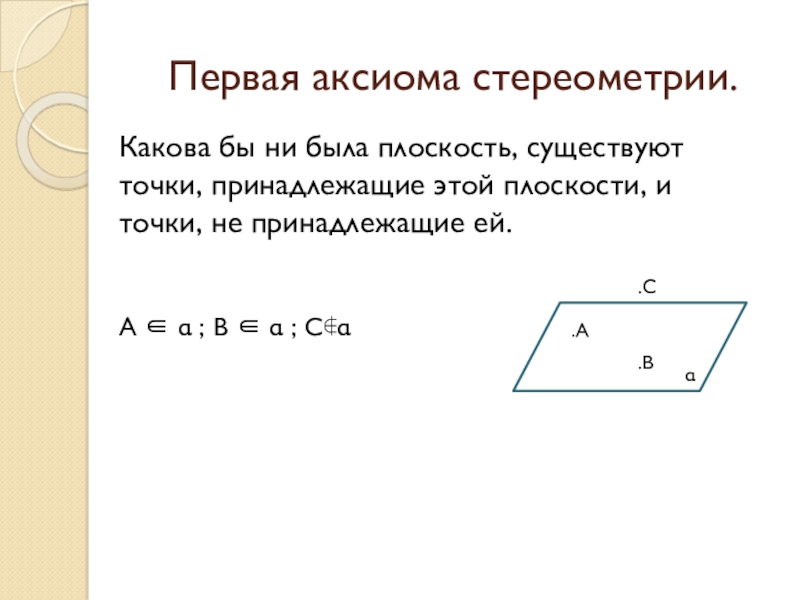
Слайд 3Первая аксиома стереометрии.
Какова бы ни была плоскость, существуют точки, принадлежащие этой
А ∈ α ; В ∈ α ; С∉α
α
.А
.В
.С
Слайд 4Вторая аксиома стереометрии.
Если две различные плоскости имеют общую точку, то они
Этой аксиомой утверждается, что если две различные плоскости α и β имеют общую точку, то существует
прямая a, принадлежащая каждой из этих
плоскостей. При этом если точка М
принадлежит обеим плоскостям, то она
принадлежит прямой a.
Слайд 5Третья аксиома стереометрии.
Если две различны прямые имеют общую точку, то
Это значит, что если две различные прямые а и в имеют общую точку С , то существует плоскость α , содержащая прямые а и в. Плоскость обладающая этим свойством , единственна.
а
в
С
α
Слайд 6Решение задач.
Задача 1.
Точки A,B,C,D не лежат в одной плоскости. Докажите, что
A
C
B
D
Решение:
Допустим, что AB и CD пересекаются. Тогда по аксиоме 3 (C3) , через них можно провести плоскость и в ней лежат все четыре точки, что противоречит условию задачи. Следовательно AB и CD не пересекаются.
ч.т.д.
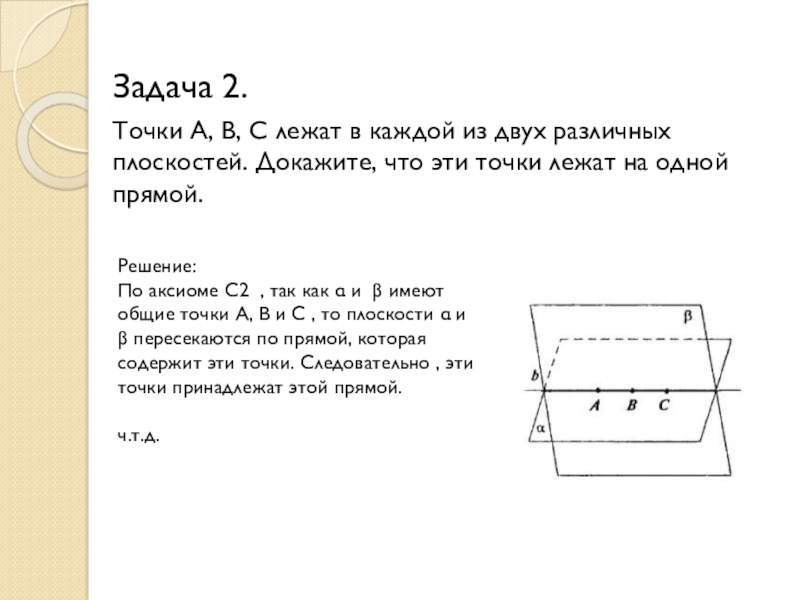
Слайд 7Задача 2.
Точки A, B, C лежат в каждой из двух различных
Решение:
По аксиоме C2 , так как α и β имеют общие точки A, B и C , то плоскости α и β пересекаются по прямой, которая содержит эти точки. Следовательно , эти точки принадлежат этой прямой.
ч.т.д.
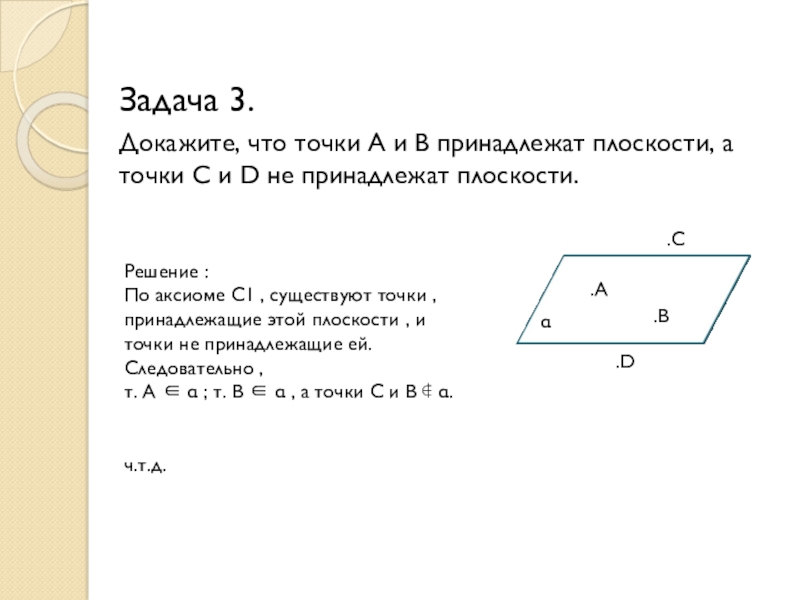
Слайд 8Задача 3.
Докажите, что точки A и B принадлежат плоскости, а точки
.A
.B
.C
.D
Решение :
По аксиоме C1 , существуют точки , принадлежащие этой плоскости , и точки не принадлежащие ей. Следовательно ,
т. A ∈ α ; т. B ∈ α , а точки C и B ∉ α.
ч.т.д.
α