Часть вторая. Задание № 25
МБОУ «Обоянская СОШ №1»
учитель математики первой категории: Черникова Е.Ю.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по подготовке к ОГЭ. Модуль геометрия
Содержание
- 1. Презентация по подготовке к ОГЭ. Модуль геометрия
- 2. Признаки равенства треугольниковПо двум сторонам и углу
- 3. Признаки подобия треугольников
- 4. Четырехугольник, у которого две стороны параллельны, а
- 5. ОкружностьОАОА - радиус окружности (r);СВ - диаметр
- 6. Задание 25.В параллелограмме АВСД точка Е –
- 7. Задание 25. Основания ВС и AD трапеции ABCD
- 8. Задание 25 На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны
- 9. Задание 25 Докажите, что биссектрисы углов при основании равнобедренного треугольника равны.
- 10. 25.В окружности с центром О проведены две
- 11.
- 12. 25. В равностороннем треугольнике ABC точки M, N,
- 13. 25. В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.
- 14. 25. Сторона BC параллелограмма ABCD вдвое больше стороны CD. Точка L — середина стороны BC. Докажите, что DL — биссектриса угла CDA.Решение.
- 15. 25. Биссектрисы углов C и D трапеции ABCD пересекаются в точке P, лежащей на стороне AB. Докажите, что точка P равноудалена от прямых BC, CD и AD.Решение.
- 16. Спасибо за внимание!
Признаки равенства треугольниковПо двум сторонам и углу между нимиПо стороне и двум прилежащим к ней угламПо трём сторонам
Слайд 1 Подготовка к ОГЭ
Модуль «Геометрия»
Слайд 2Признаки равенства треугольников
По двум сторонам и углу между ними
По стороне и
двум прилежащим к ней углам
По трём сторонам
Слайд 4Четырехугольник, у которого две стороны параллельны, а две другие нет, называется
трапецией.
A
B
C
D
BC, AD–основания трапеции, ВС║АD
AB,CD – боковые стороны
Трапеция
M
N
MN –средняя линия трапеции
Свойства
средней линии трапеции:
P = АВ+ВС+СD+AD
Основные формулы
a
b
h
В равнобедренной трапеции углы при основаниях равны
В равнобедренной трапеции диагонали равны
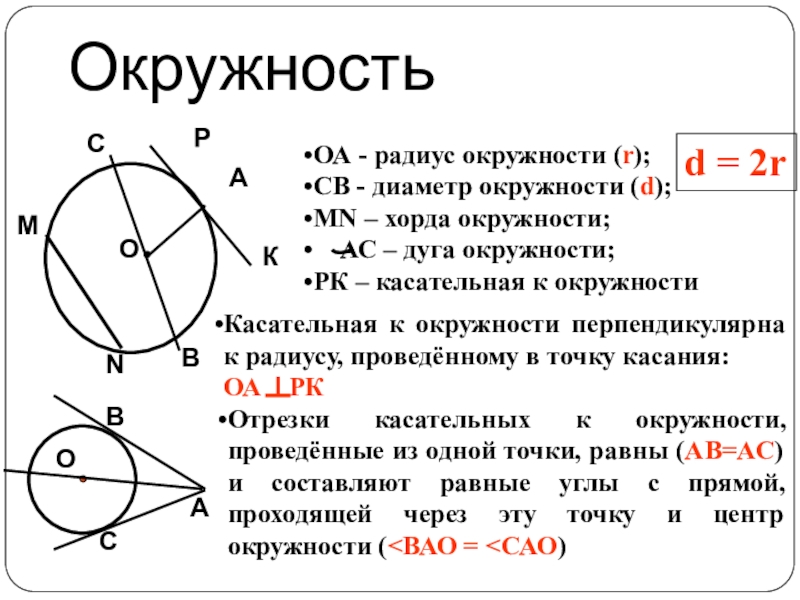
Слайд 5Окружность
О
А
ОА - радиус окружности (r);
СВ - диаметр окружности (d);
MN – хорда
окружности;
АС – дуга окружности;
РК – касательная к окружности
АС – дуга окружности;
РК – касательная к окружности
С
В
М
N
Р
К
Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания:
ОА РК
Отрезки касательных к окружности, проведённые из одной точки, равны (АВ=АС) и составляют равные углы с прямой, проходящей через эту точку и центр окружности (<ВАО = <САО)
d = 2r
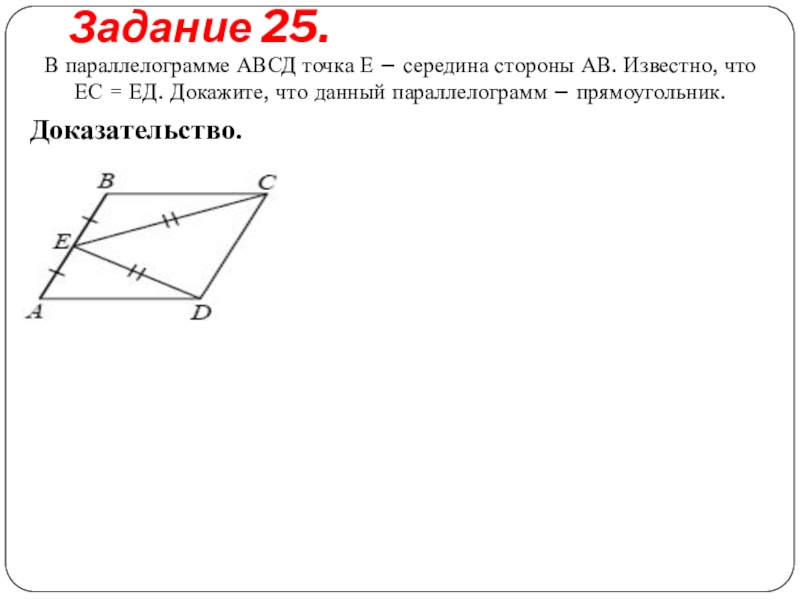
Слайд 6Задание 25.
В параллелограмме АВСД точка Е – середина стороны АВ. Известно,
что ЕС = ЕД. Докажите, что данный параллелограмм – прямоугольник.
Доказательство.
Доказательство.
Слайд 7Задание 25. Основания ВС и AD трапеции ABCD равны соответственно 3 и
12, BD = 6. Докажите, что треугольники CBD и BDA подобны.
Слайд 8Задание 25
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что
отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
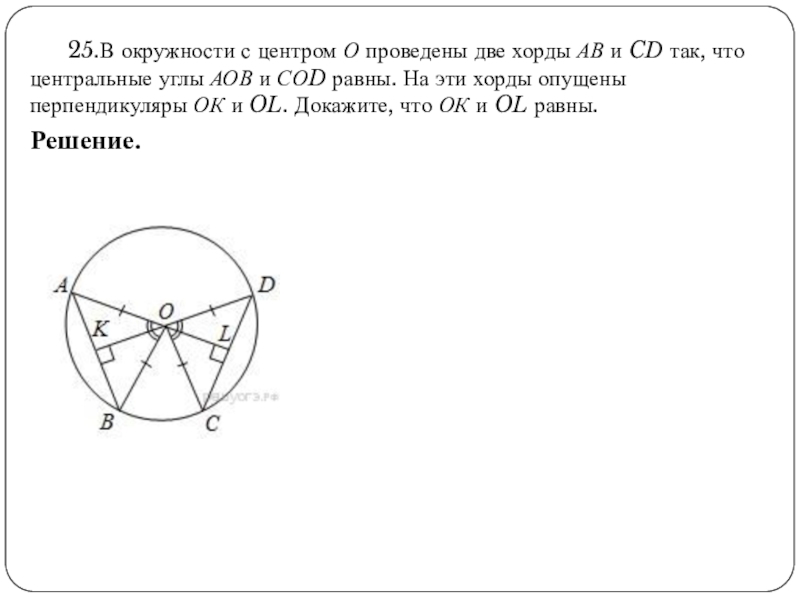
Слайд 10 25.В окружности с центром О проведены две хорды АВ и CD так, что центральные углы АОВ и СОD равны.
На эти хорды опущены перпендикуляры ОК и OL. Докажите, что ОК и OL равны.
Решение.
Решение.
Слайд 11
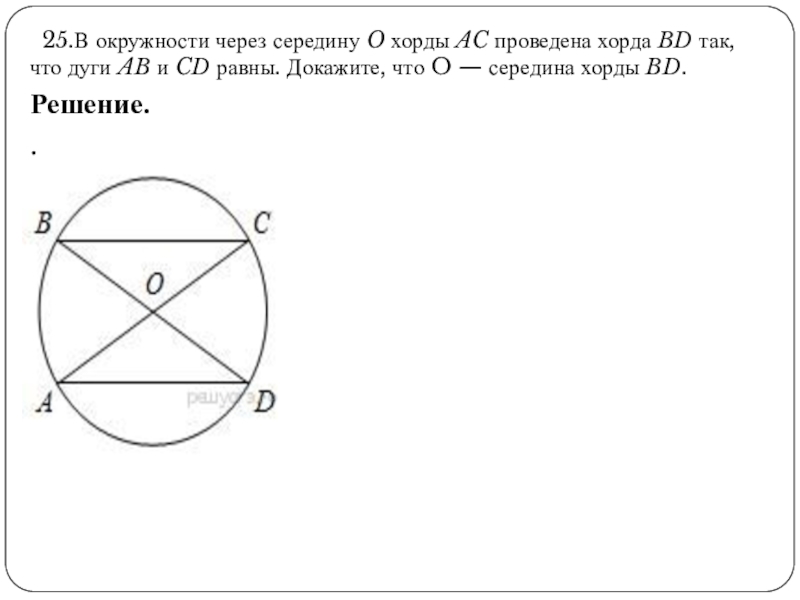
25.В окружности через середину O хорды AC проведена хорда BD так, что дуги AB и CD равны. Докажите, что
O — середина хорды BD.
Решение.
.
Решение.
.
Слайд 12
25. В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА
соответственно. Докажите, что треугольник MNK — равносторонний.
Решение.
Решение.
Слайд 13 25. В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.
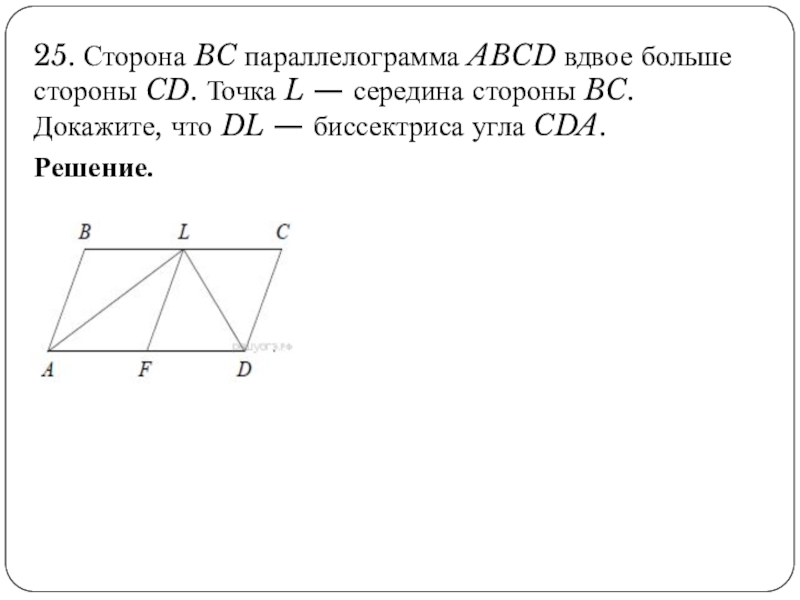
Слайд 1425. Сторона BC параллелограмма ABCD вдвое больше стороны CD. Точка L — середина стороны BC. Докажите, что DL — биссектриса угла CDA.
Решение.
Слайд 15 25. Биссектрисы углов C и D трапеции ABCD пересекаются в точке P, лежащей на стороне AB. Докажите, что
точка P равноудалена от прямых BC, CD и AD.
Решение.
Решение.
