- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Задачи на построение сечений для 10 класса
Содержание
- 1. Презентация по математике Задачи на построение сечений для 10 класса
- 2. Презентация по геометрии учителя математики МКОУ СОШ
- 3. Секущей плоскостью тетраэдра (параллелепипеда) называется любая плоскость,
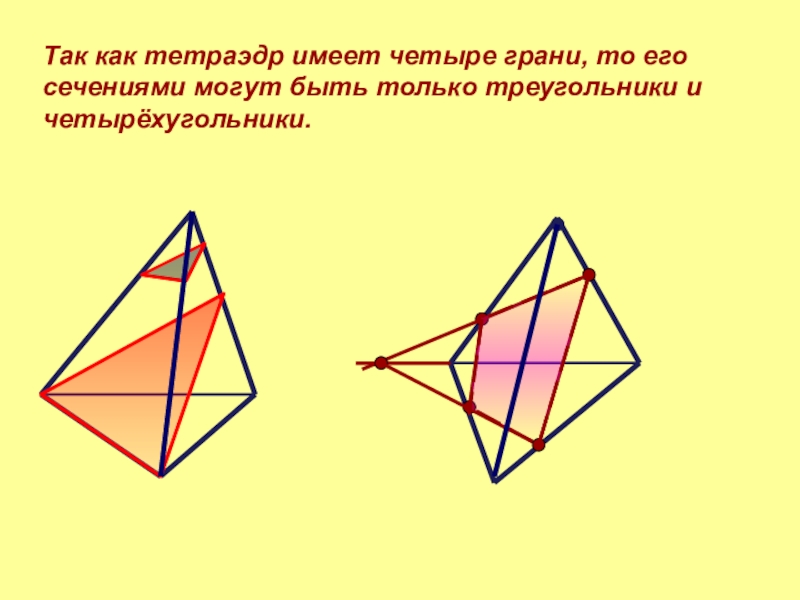
- 4. Так как тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники.
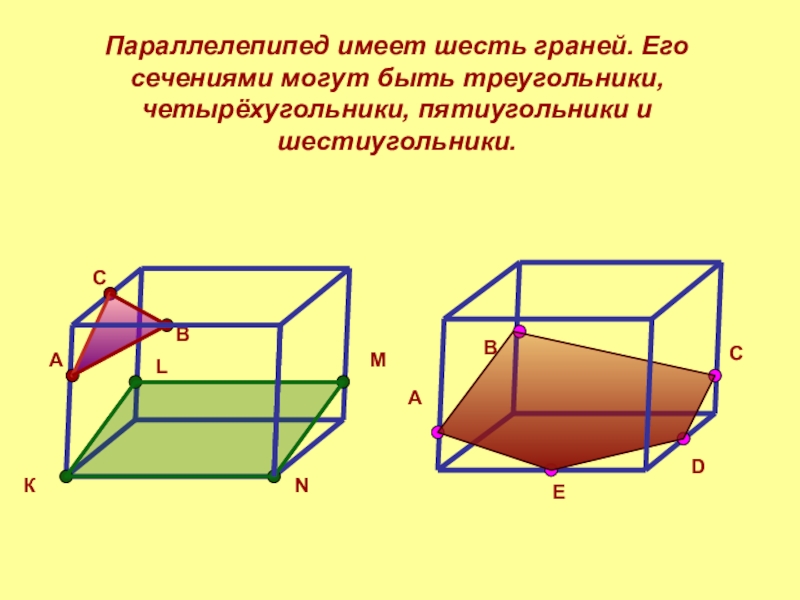
- 5. Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники.АВСКNLMАВСDE
- 6. Задача 1: На рёбрах AB, BD и
- 7. 2 случай: прямые NP ll BC.ABCDNPMQЕсли NP
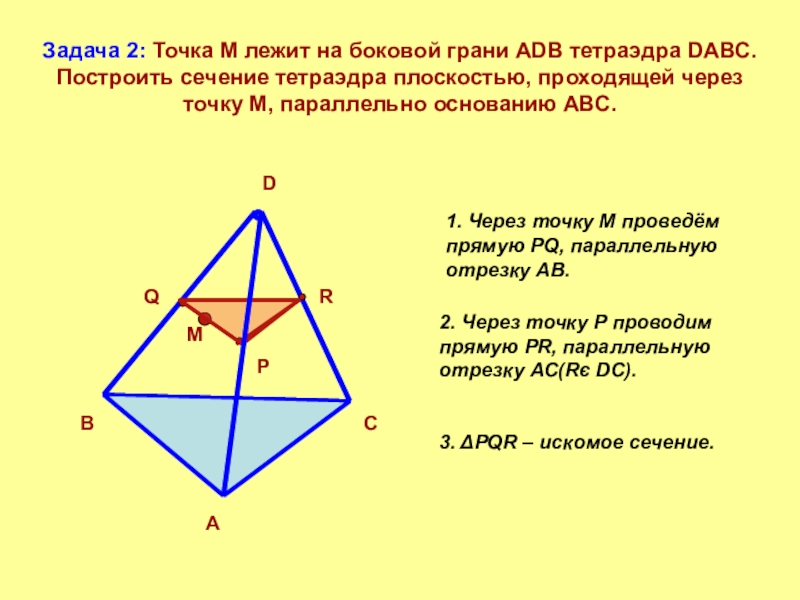
- 8. Задача 2: Точка М лежит на боковой
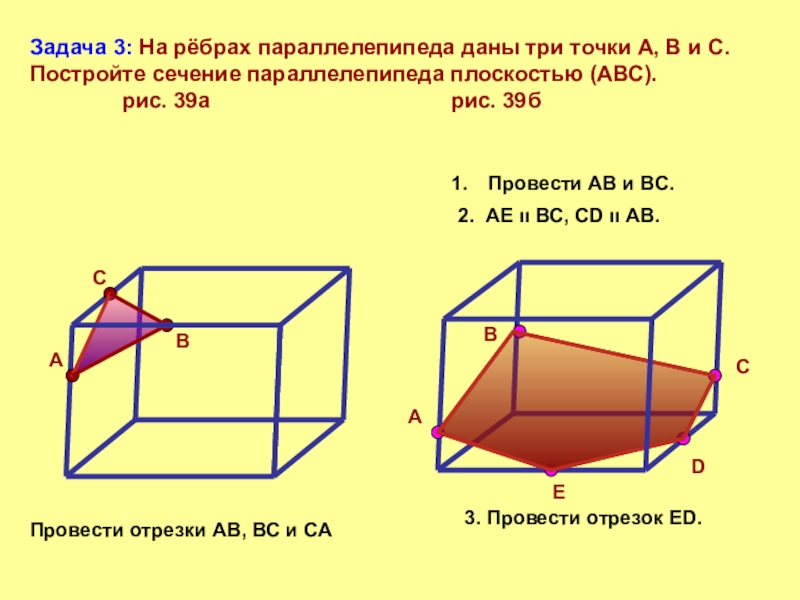
- 9. Задача 3: На рёбрах параллелепипеда даны три
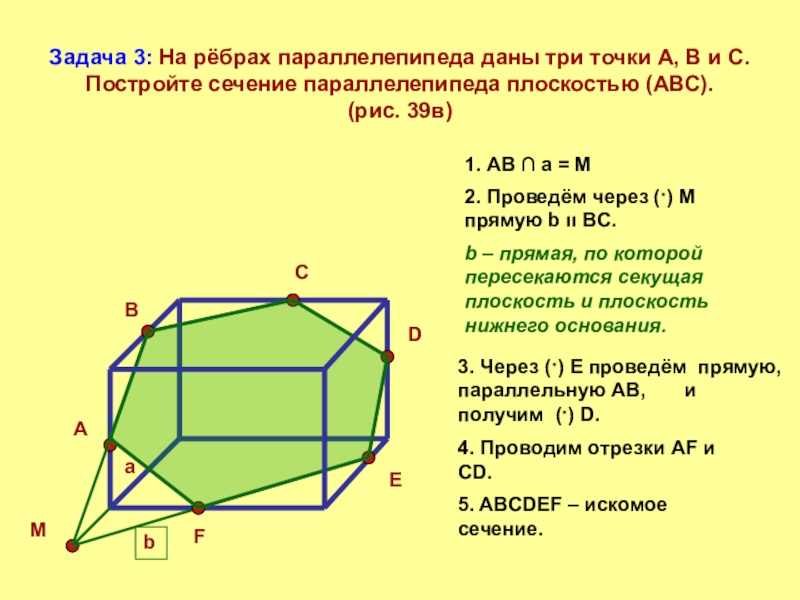
- 10. Задача 3: На рёбрах параллелепипеда даны три
- 11. Решение задач на построение сечений
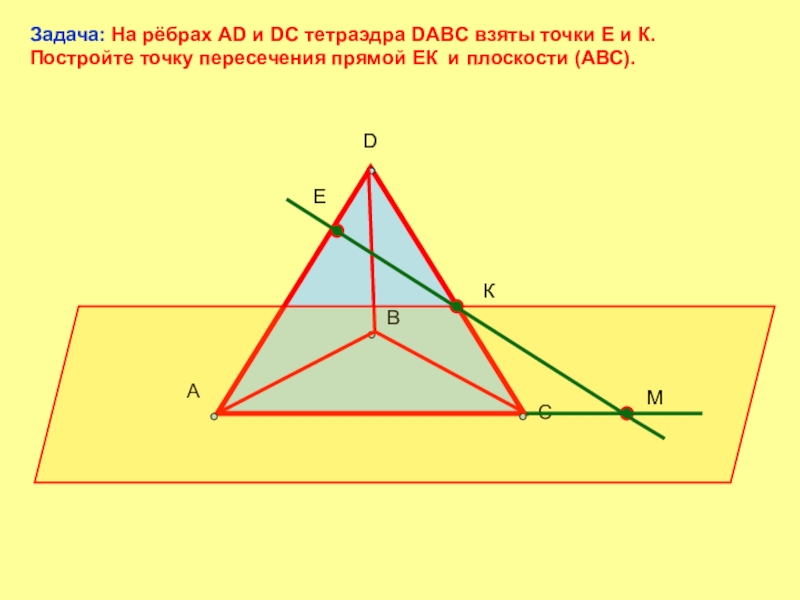
- 12. DАВСЕКМЗадача: На рёбрах AD и DC тетраэдра
- 13. АВСDА1В1С1D1№ 81: М є ВВ1, Nє СС1.
- 14. АВСDА1В1С1D1№ 82в: М є (АА1В1). Постройте сечение,
- 15. АВСDА1В1С1D1№ 83: Постройте сечение, проходящее: а) через
- 16. АВСDА1В1С1D1МКLNO1. Построим KL ll AD,где (·) M
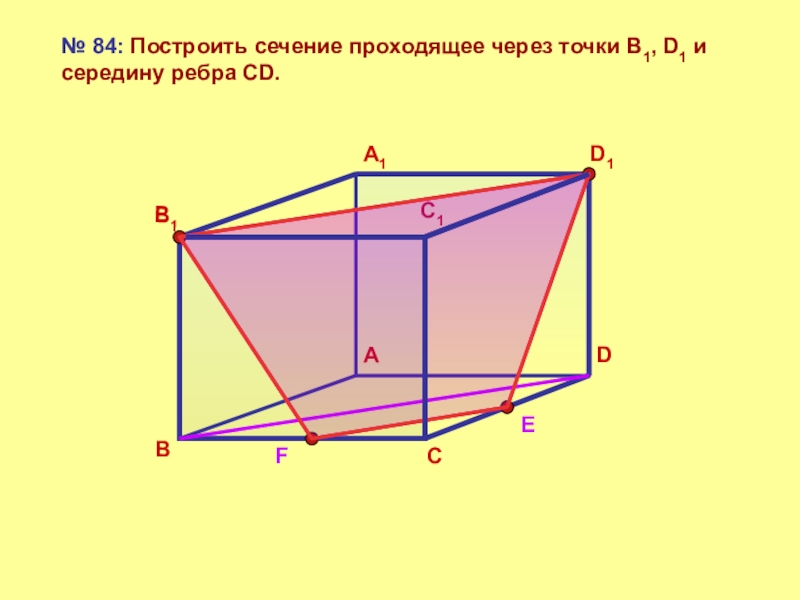
- 17. ВАDСВ1А1D1С1№ 84: Построить сечение проходящее через точки B1, D1 и середину ребра CD. FE
- 18. АDСВА1D1С1В1№ 85: Построить сечение (BKL), где К
- 19. АDСВА1D1С1В1№ 86: Построить сечение проходящее через диагональ
- 20. DABCD1A1B1C1№ 87а: Постройте сечение плоскостью (MNK), где
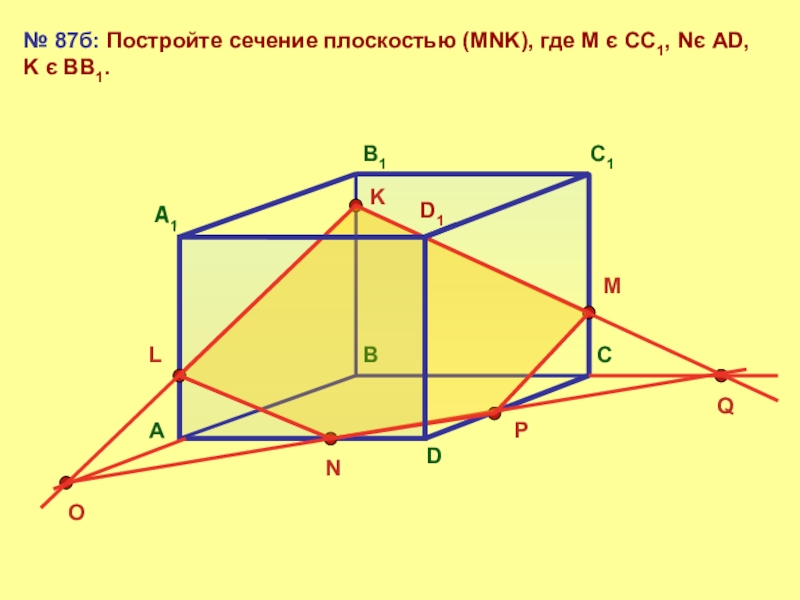
- 21. АВСDА1В1С1D1№ 87б: Постройте сечение плоскостью (MNK), где М є СС1, Nє AD, K є BB1.MNKLOPQ
Слайд 2Презентация по геометрии учителя математики МКОУ СОШ №1 Розовой С М пгт. Палана Камчатский край Учебник геометрии
Слайд 3Секущей плоскостью тетраэдра (параллелепипеда) называется любая плоскость, по обе стороны от
Секущая плоскость пересекает грани многогранника по отрезкам.
Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника (тетраэдра, параллелепипеда).
Слайд 4
Так как тетраэдр имеет четыре грани, то его сечениями могут быть
Слайд 5Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырёхугольники, пятиугольники
А
В
С
К
N
L
M
А
В
С
D
E
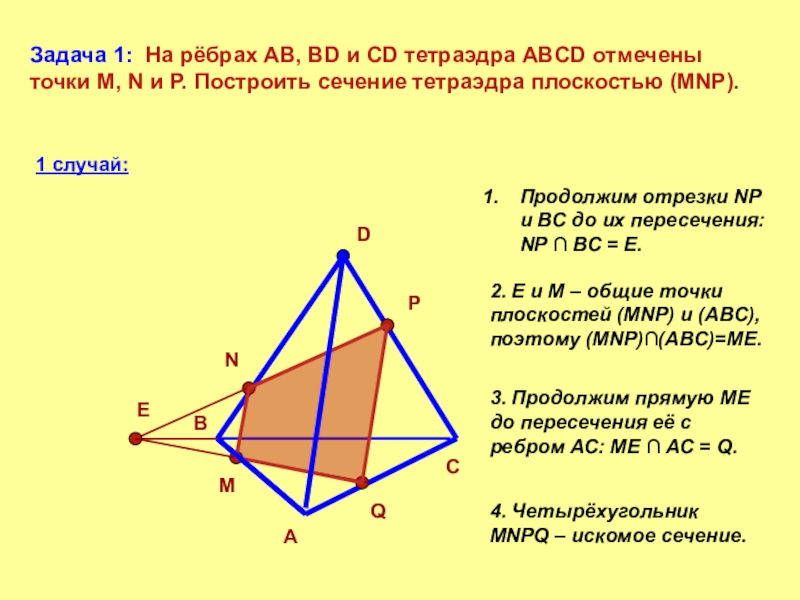
Слайд 6Задача 1: На рёбрах AB, BD и CD тетраэдра ABCD отмечены
1 случай:
М
N
P
Продолжим отрезки NP и BC до их пересечения: NP ∩ BC = E.
E
2. Е и М – общие точки плоскостей (MNP) и (ABC), поэтому (MNP)∩(ABC)=МЕ.
3. Продолжим прямую МЕ до пересечения её с ребром АС: МЕ ∩ АС = Q.
Q
4. Четырёхугольник MNPQ – искомое сечение.
А
С
D
B
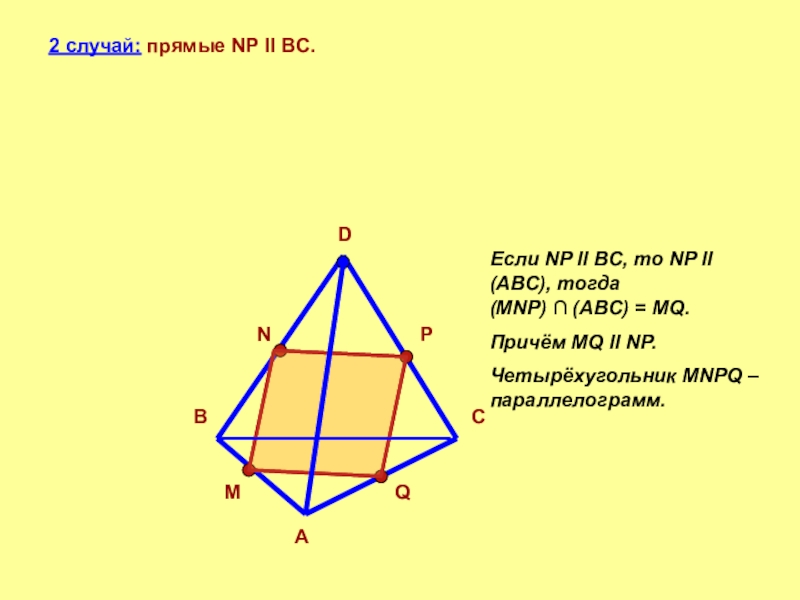
Слайд 72 случай: прямые NP ll BC.
A
B
C
D
N
P
M
Q
Если NP ll BC, то NP
Причём MQ ll NP.
Четырёхугольник MNPQ – параллелограмм.
Слайд 8Задача 2: Точка М лежит на боковой грани АDВ тетраэдра DАВС.
А
В
С
D
М
1. Через точку М проведём прямую PQ, параллельную отрезку АВ.
Р
Q
2. Через точку Р проводим прямую PR, параллельную отрезку АС(Rє DC).
R
3. ΔPQR – искомое сечение.
Слайд 9Задача 3: На рёбрах параллелепипеда даны три точки А, В и
А
В
С
А
В
С
D
E
Провести отрезки АВ, ВС и СА
Провести АВ и ВС.
2. АЕ ıı ВС, СD ıı АВ.
3. Провести отрезок ЕD.
Слайд 10Задача 3: На рёбрах параллелепипеда даны три точки А, В и
А
В
С
а
1. АВ ∩ а = М
М
2. Проведём через (·) М прямую b ıı ВС.
b
F
E
b – прямая, по которой пересекаются секущая плоскость и плоскость нижнего основания.
3. Через (·) Е проведём прямую, параллельную АВ, и получим (·) D.
D
4. Проводим отрезки AF и CD.
5. ABCDEF – искомое сечение.
Слайд 12
D
А
В
С
Е
К
М
Задача: На рёбрах AD и DC тетраэдра DABC взяты точки Е
Слайд 13
А
В
С
D
А1
В1
С1
D1
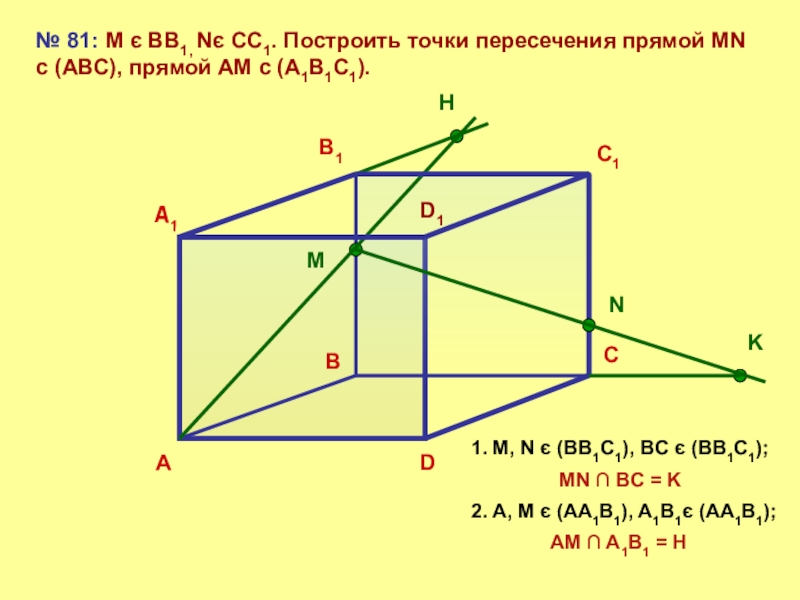
№ 81: М є ВВ1, Nє СС1. Построить точки пересечения прямой
М
N
K
H
1. M, N є (BB1C1), BC є (BB1C1);
MN ∩ BC = K
2. A, M є (AA1B1), A1B1є (AA1B1);
AM ∩ A1B1 = H
Слайд 14
А
В
С
D
А1
В1
С1
D1
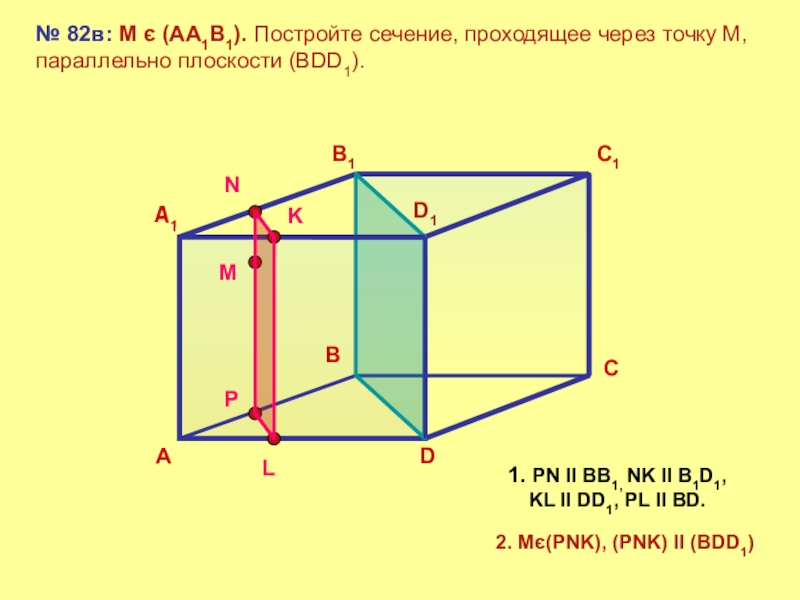
№ 82в: М є (АА1В1). Постройте сечение, проходящее через точку М,
M
N
P
K
L
1. PN ll BB1, NK ll B1D1, KL ll DD1, PL ll BD.
2. Mє(PNK), (PNK) ll (BDD1)
Слайд 15
А
В
С
D
А1
В1
С1
D1
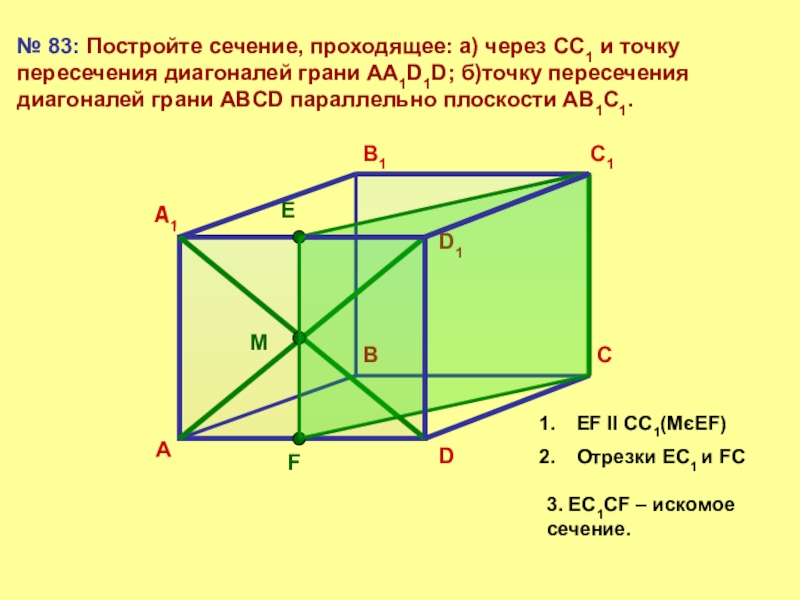
№ 83: Постройте сечение, проходящее: а) через СС1 и точку пересечения
М
Е
F
EF ll CC1(MєEF)
Отрезки EC1 и FC
3. ЕС1СF – искомое сечение.
Слайд 16
А
В
С
D
А1
В1
С1
D1
М
К
L
N
O
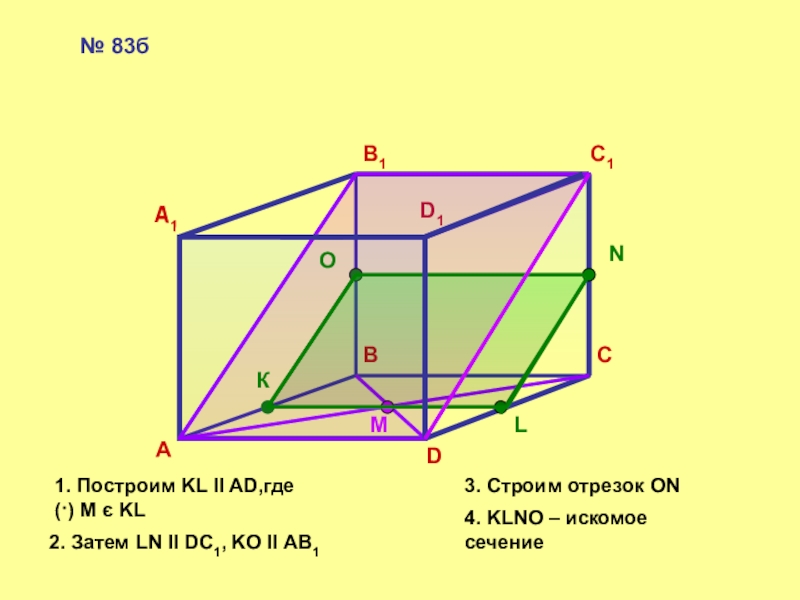
1. Построим KL ll AD,где (·) M є KL
2. Затем LN
3. Строим отрезок ON
4. KLNO – искомое сечение
№ 83б
Слайд 18
А
D
С
В
А1
D1
С1
В1
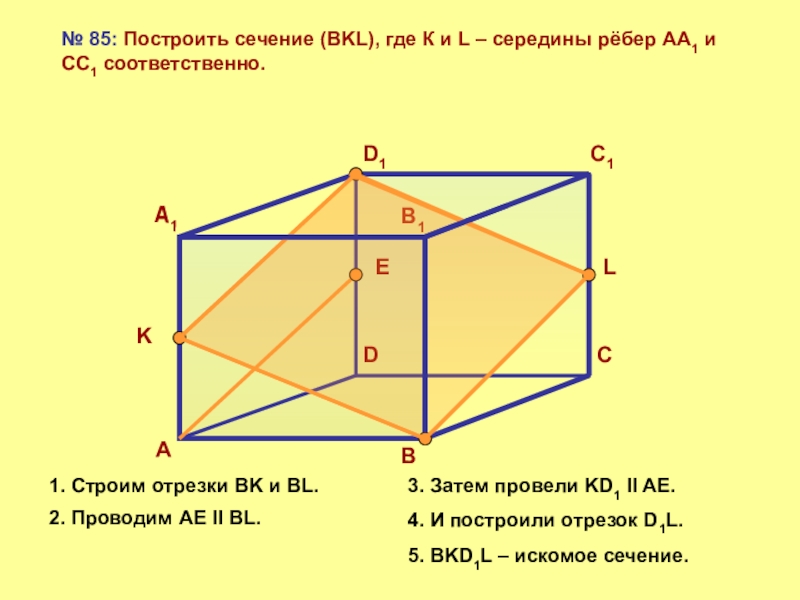
№ 85: Построить сечение (BKL), где К и L – середины
K
L
E
1. Строим отрезки BK и BL.
2. Проводим AE ll BL.
3. Затем провели KD1 ll AE.
4. И построили отрезок D1L.
5. BKD1L – искомое сечение.
Слайд 19
А
D
С
В
А1
D1
С1
В1
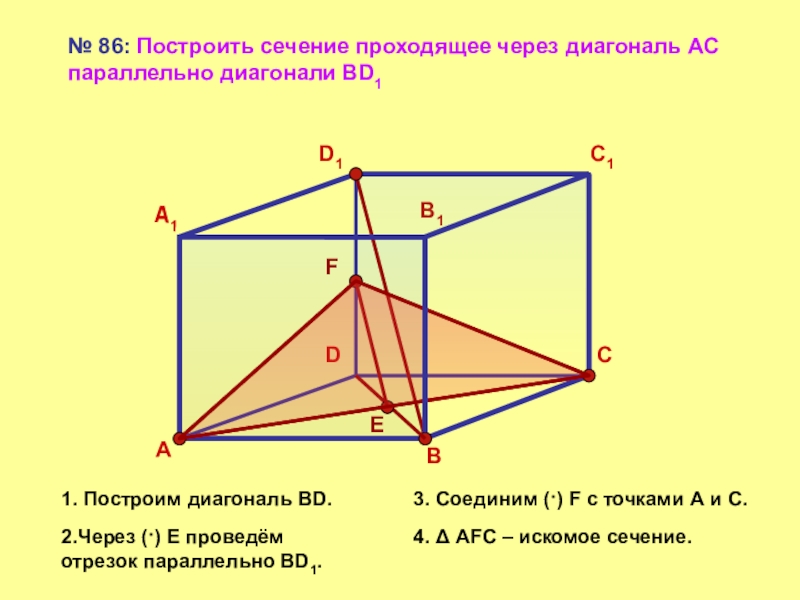
№ 86: Построить сечение проходящее через диагональ АС параллельно диагонали BD1
1.
E
2.Через (·) Е проведём отрезок параллельно BD1.
F
3. Соединим (·) F c точками А и С.
4. Δ AFC – искомое сечение.
Слайд 20
D
A
B
C
D1
A1
B1
C1
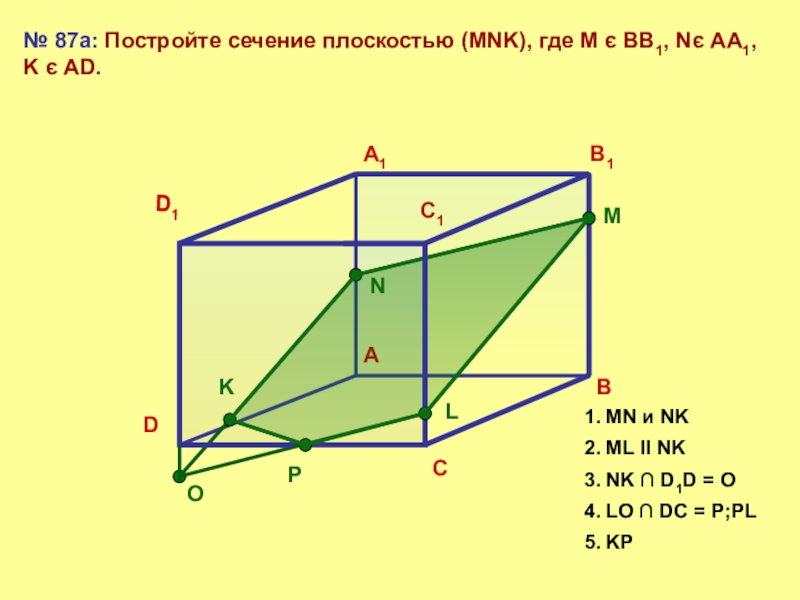
№ 87а: Постройте сечение плоскостью (MNK), где М є ВВ1, Nє
K
N
L
M
O
P
1. MN и NK
2. ML ll NK
3. NK ∩ D1D = O
4. LO ∩ DC = P;PL
5. KP