Ковров, Владимирская область.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Треугольники (9 класс)
Содержание
- 1. Презентация по математике Треугольники (9 класс)
- 2. ТреугольникиТреугольник – геометрическая фигура, состоящая из трех
- 3. Виды треугольниковПо сторонамРазностороннийРавнобедренныйРавностороннийПо угламостроугольныйтупоугольныйПрямоугольный
- 4. ТреугольникиМедиана треугольника – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
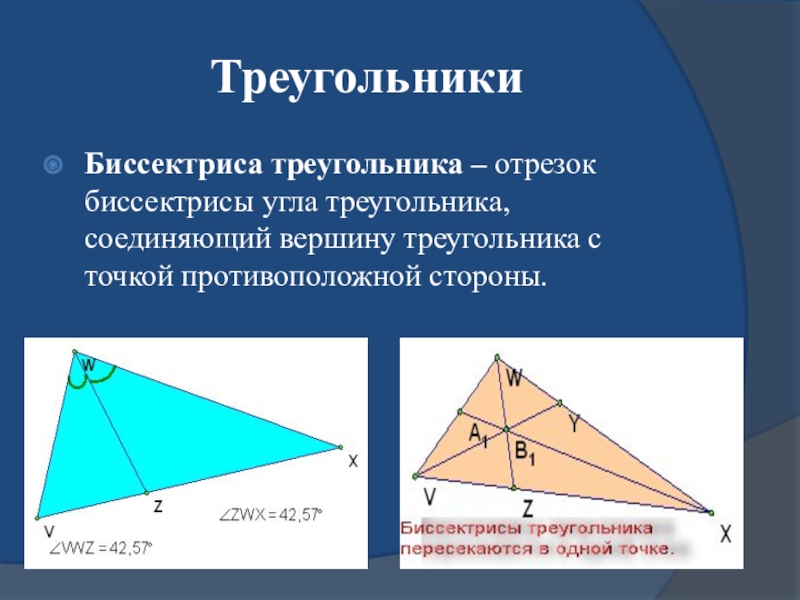
- 5. ТреугольникиБиссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
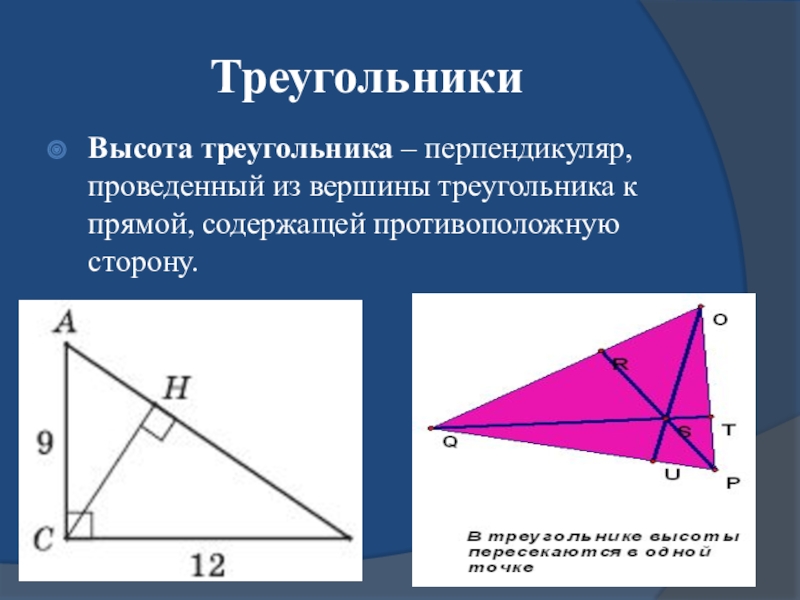
- 6. ТреугольникиВысота треугольника – перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
- 7. Слайд 7
- 8. Слайд 8
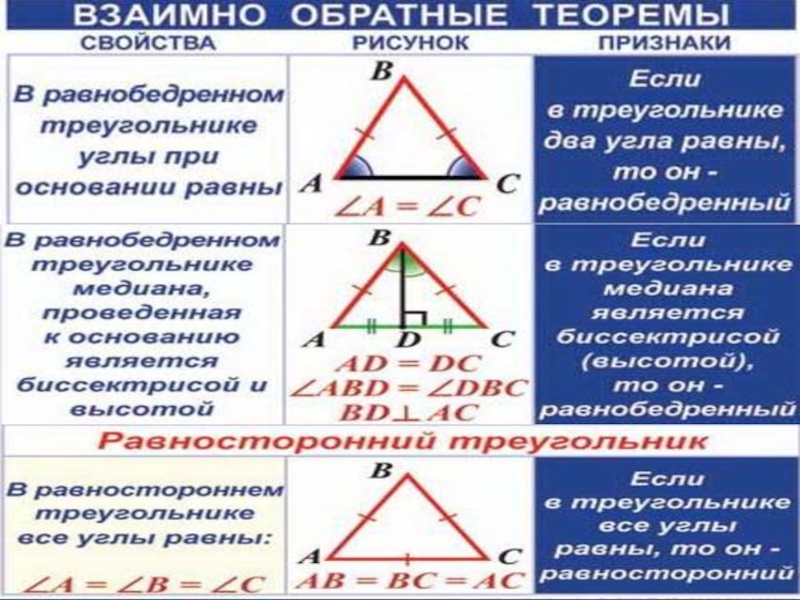
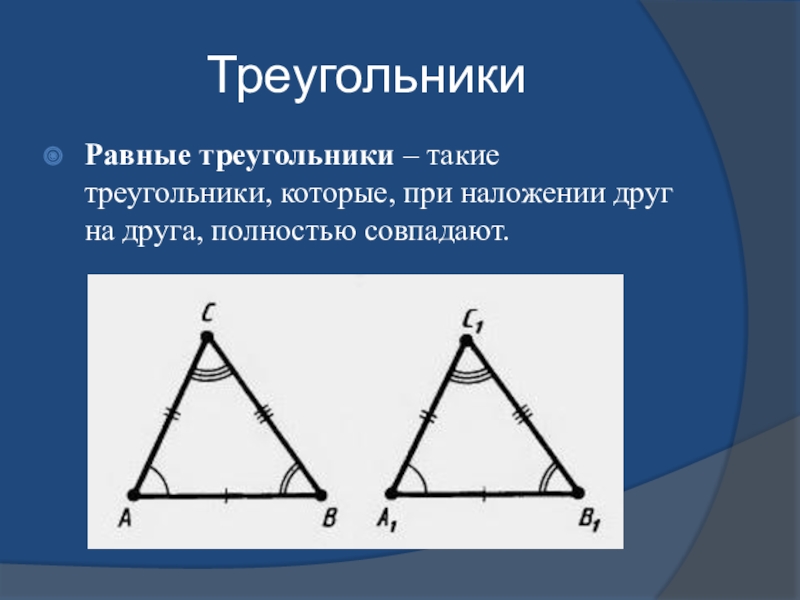
- 9. ТреугольникиРавные треугольники – такие треугольники, которые, при наложении друг на друга, полностью совпадают.
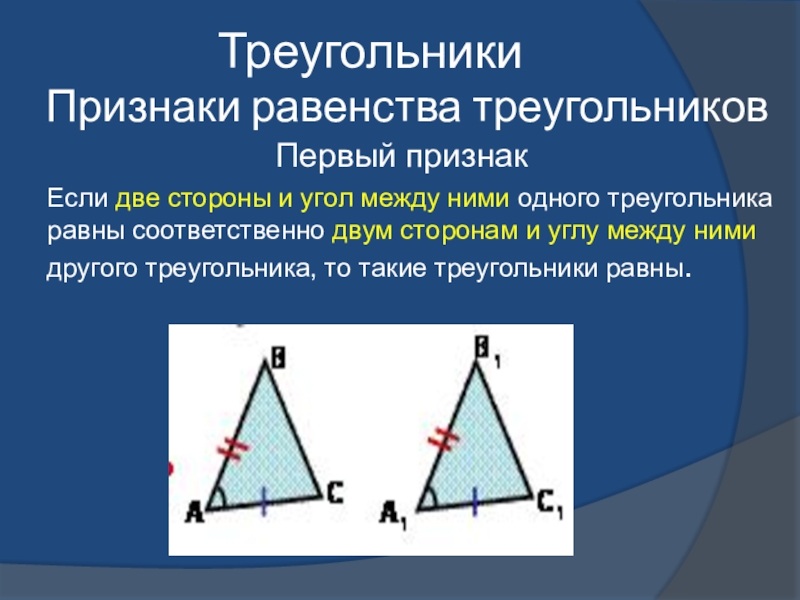
- 10. ТреугольникиПризнаки равенства треугольниковПервый признакЕсли две стороны и
- 11. ТреугольникиПризнаки равенства треугольниковВторой признакЕсли сторона и
- 12. Признаки равенства треугольниковТретий признакЕсли три стороны одного
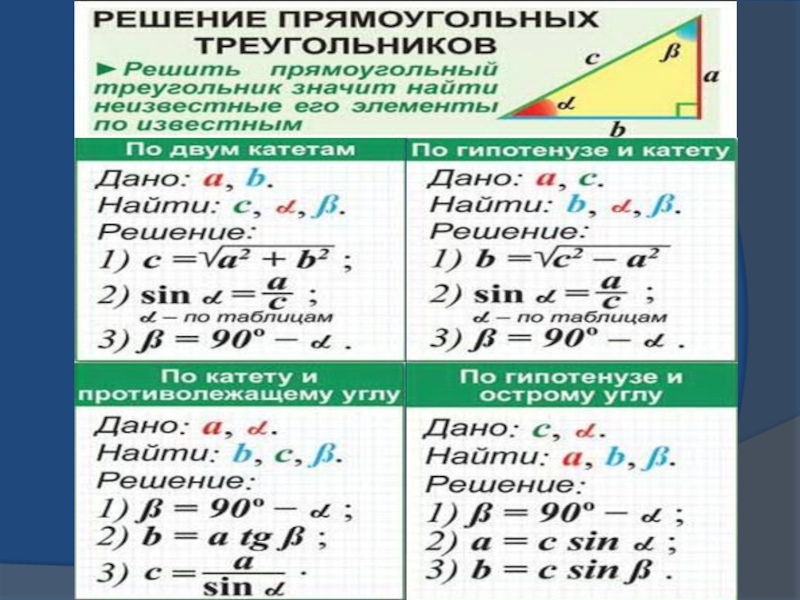
- 13. Прямоугольный треугольник ОпределениеТреугольник называется прямоугольным, если один из его углов прямой.С=900АС, СВ- катетыАВ- гипотенуза
- 14. Свойства прямоугольного треугольника:1. Сумма острых углов прямоугольного
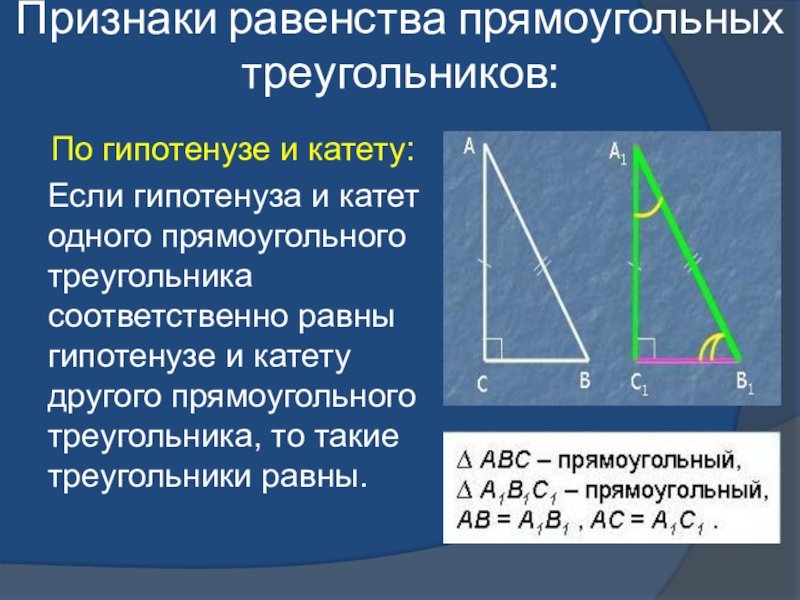
- 15. Признаки равенства прямоугольных треугольников:По гипотенузе и катету:
- 16. По двум катетам:Если два катета одного прямоугольного
- 17. По катету и прилежащему острому углу:Если катет
- 18. По гипотенузе и острому углу:Если гипотенуза и
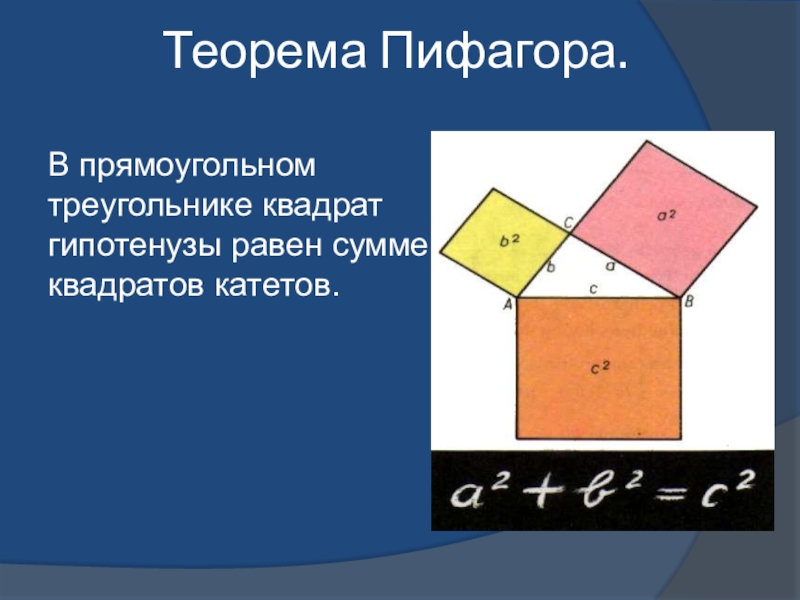
- 19. Теорема Пифагора.В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
- 20. Слайд 20
- 21. Подобные треугольники – это такие треугольники, у
- 22. Признаки подобия треугольников:1.Если два угла одного треугольника
- 23. Сумма углов треугольника.Сумма углов треугольника равна 1800А + В + С = 1800
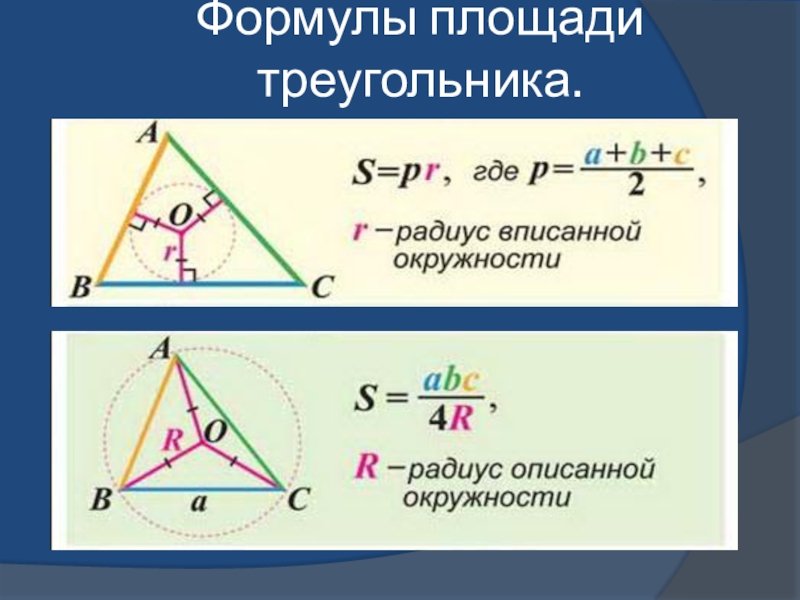
- 24. Формулы площади треугольника.
- 25. Формулы площади треугольника.
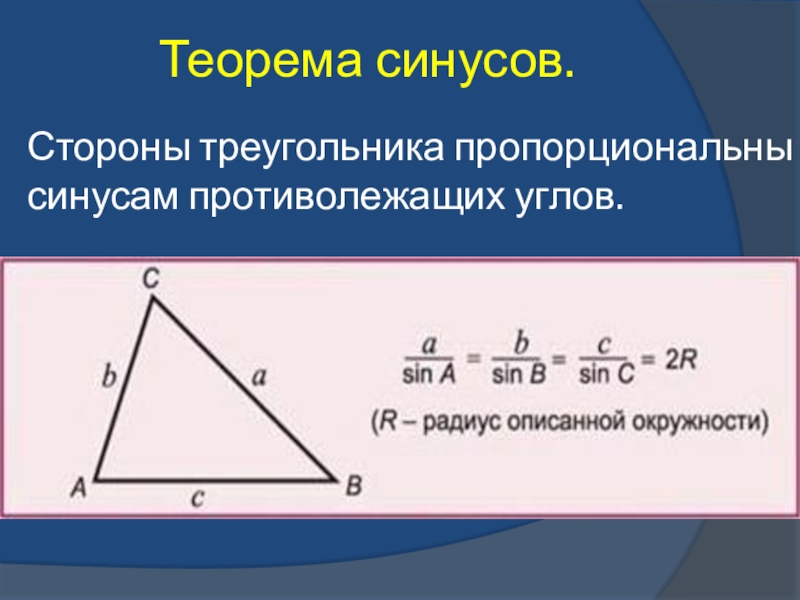
- 26. Теорема синусов.Стороны треугольника пропорциональны синусам противолежащих углов.
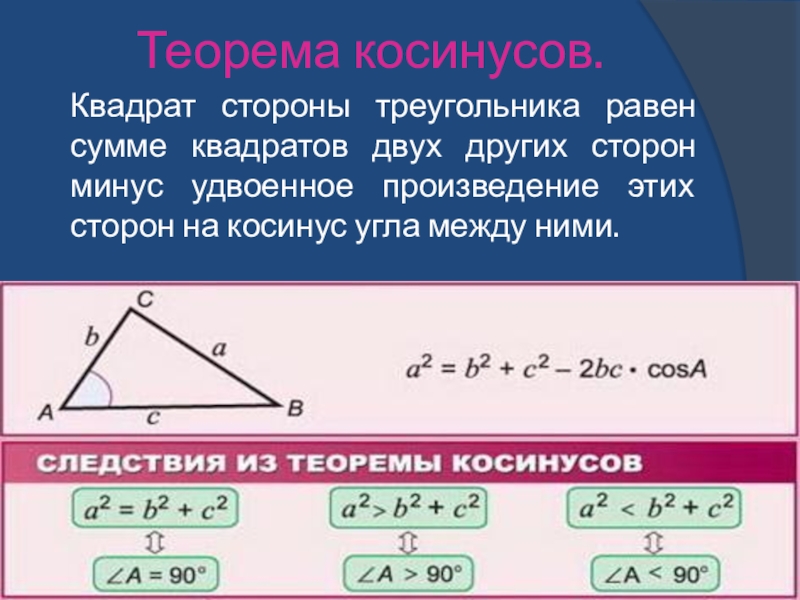
- 27. Теорема косинусов.Квадрат стороны треугольника равен сумме квадратов
- 28. Слайд 28
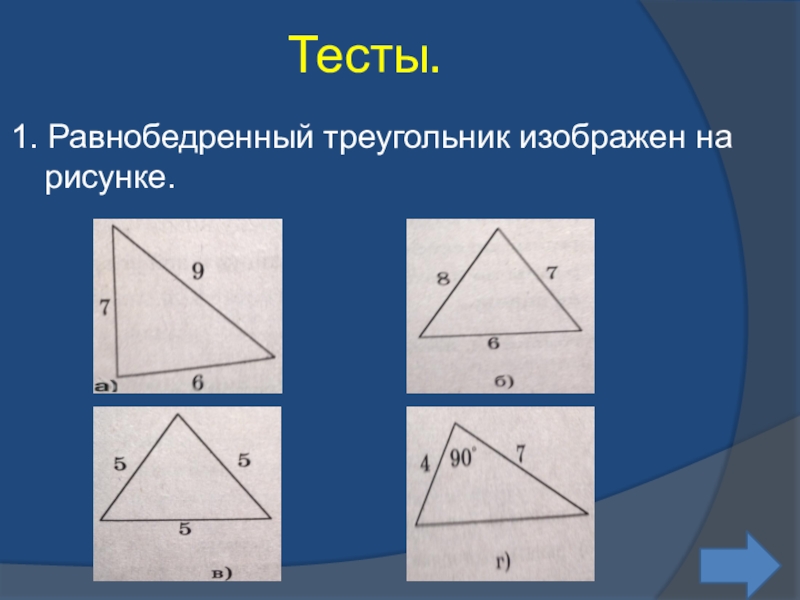
- 29. Тесты.1. Равнобедренный треугольник изображен на рисунке.
- 30. Верно!
- 31. Неверно!
- 32. Неверно!
- 33. Неверно!
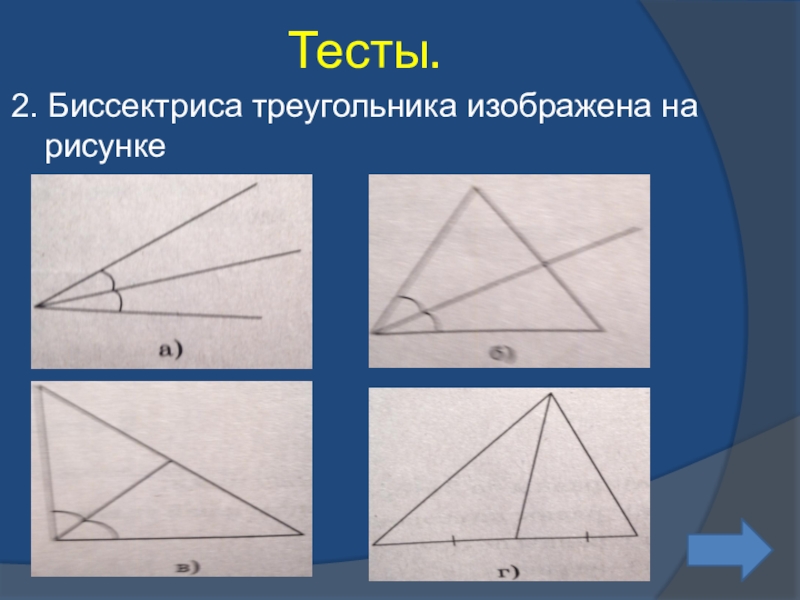
- 34. 2. Биссектриса треугольника изображена на рисункеТесты.
- 35. Верно!
- 36. Неверно!
- 37. Неверно!
- 38. Неверно!
- 39. а) Равны по 2 сторонам и углу
- 40. Верно!
- 41. Неверно!
- 42. Неверно!
- 43. Неверно!
- 44. Тесты.4. Треугольники изображенные на рисунке,а) Равны по
- 45. Верно!
- 46. Неверно!
- 47. Неверно!
- 48. Неверно!
- 49. а) Равны по 2 сторонам и углу
- 50. Верно!
- 51. Неверно!
- 52. Неверно!
- 53. Неверно!
- 54. 6. Треугольники изображенные на рисунке,Тесты.а) Равны по
- 55. Верно!
- 56. Неверно!
- 57. Неверно!
- 58. Неверно!
- 59. Тесты.7. Медиана треугольника изображена на рисунке.
- 60. Верно!
- 61. Неверно!
- 62. Неверно!
- 63. Неверно!
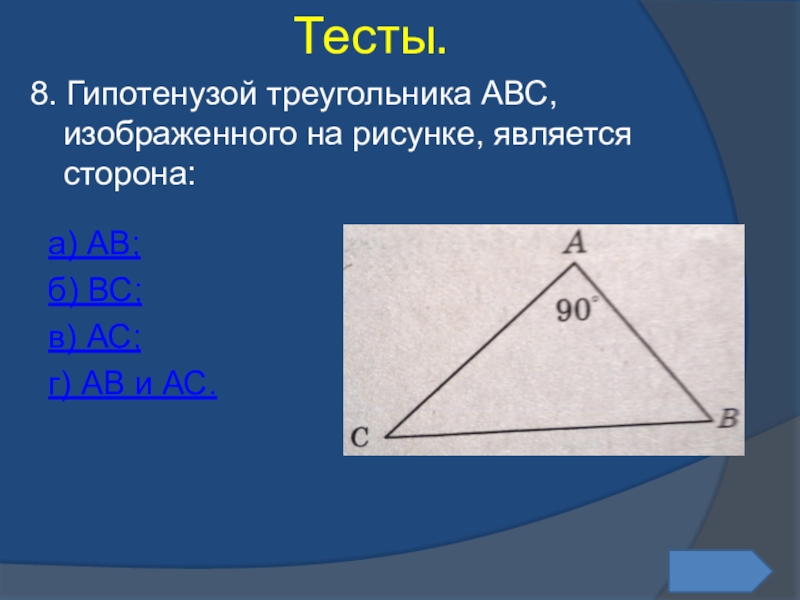
- 64. 8. Гипотенузой треугольника АВС, изображенного на рисунке, является сторона:Тесты.а) АВ;б) ВС;в) АС;г) АВ и АС.
- 65. Верно!
- 66. Неверно!
- 67. Неверно!
- 68. Неверно!
ТреугольникиТреугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, соединенных тремя отрезками. D
Слайд 2Треугольники
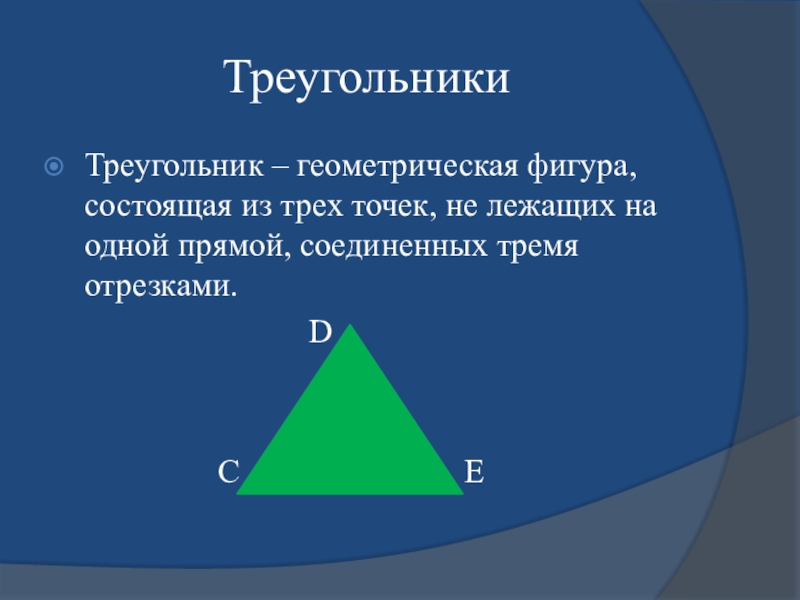
Треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на
одной прямой, соединенных тремя отрезками.
D
С E
D
С E
Слайд 3Виды треугольников
По сторонам
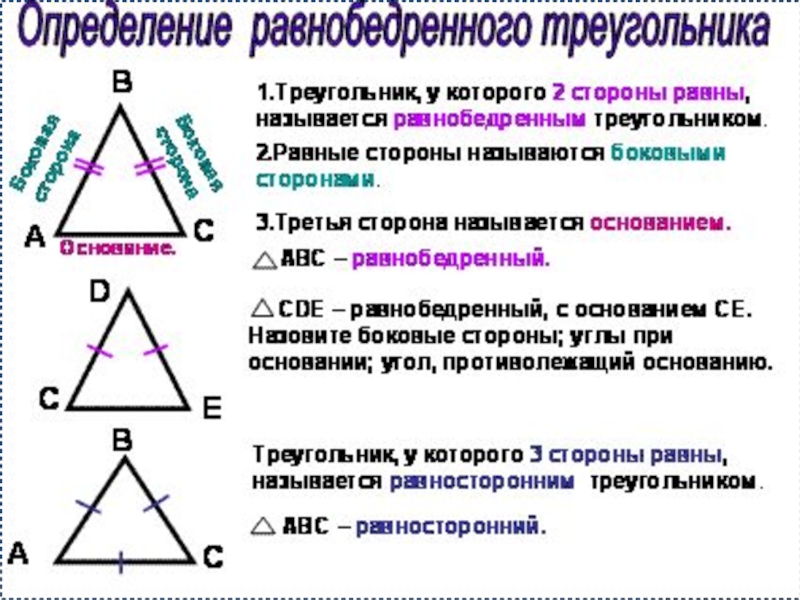
Разносторонний
Равнобедренный
Равносторонний
По углам
остроугольный
тупоугольный
Прямоугольный
Слайд 4Треугольники
Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Слайд 5Треугольники
Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с
точкой противоположной стороны.
Слайд 6Треугольники
Высота треугольника – перпендикуляр, проведенный из вершины треугольника к прямой, содержащей
противоположную сторону.
Слайд 9Треугольники
Равные треугольники – такие треугольники, которые, при наложении друг на друга,
полностью совпадают.
Слайд 10Треугольники
Признаки равенства треугольников
Первый признак
Если две стороны и угол между ними одного
треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Слайд 11 Треугольники
Признаки равенства треугольников
Второй признак
Если сторона и два прилежащих к ней
угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Слайд 12Признаки равенства треугольников
Третий признак
Если три стороны одного треугольника равны соответственно трём
сторонам другого треугольника, то такие треугольники равны.
Треугольники
Слайд 13Прямоугольный треугольник
Определение
Треугольник называется прямоугольным, если один из его углов прямой.
С=900
АС, СВ-
катеты
АВ- гипотенуза
АВ- гипотенуза
Слайд 14Свойства прямоугольного треугольника:
1. Сумма острых углов прямоугольного треугольника равна 90°.
2. Катет,
лежащий против угла в 30° равен половине гипотенузы (и обратно).
3. Медиана, проведенная к гипотенузе, равна половине гипотенузы (равна радиусу описанной окружности.)
3. Медиана, проведенная к гипотенузе, равна половине гипотенузы (равна радиусу описанной окружности.)
Слайд 15Признаки равенства прямоугольных треугольников:
По гипотенузе и катету:
Если гипотенуза и катет
одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Слайд 16По двум катетам:
Если два катета одного прямоугольного треугольника соответственно равны двум
катетам другого прямоугольного треугольника, то такие треугольники равны.
Признаки равенства прямоугольных треугольников:
Слайд 17По катету и прилежащему острому углу:
Если катет и прилежащий к нему
острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
Признаки равенства прямоугольных треугольников:
Слайд 18По гипотенузе и острому углу:
Если гипотенуза и острый угол одного прямоугольного
треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Признаки равенства прямоугольных треугольников:
Слайд 19Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Слайд 21Подобные треугольники – это такие треугольники, у которых углы соответственно равны
и стороны одного треугольника пропорциональны сходственным сторонам другого.
Треугольники
∆АВС~∆EGF:
А=E;B=G;
C=F;
Слайд 22Признаки подобия треугольников:
1.Если два угла одного треугольника соответственно равны двум углам
другого треугольника, то такие треугольники подобны.
2.Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между этими сторонами равны, то такие треугольники подобны.
3.Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
2.Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между этими сторонами равны, то такие треугольники подобны.
3.Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Слайд 27Теорема косинусов.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус
удвоенное произведение этих сторон на косинус угла между ними.
Слайд 39а) Равны по 2 сторонам и углу между ними;
б) равны по
стороне и 2 прилежащим к ней углам;
в) равны по 3 сторонам;
г) Не равны
в) равны по 3 сторонам;
г) Не равны
Тесты.
3.Треугольники, изображенные на рисунке,
Слайд 44Тесты.
4. Треугольники изображенные на рисунке,
а) Равны по 2 сторонам и углу
между ними;
б) равны по стороне и 2 прилежащим к ней углам;
в) равны по 3 сторонам;
г) Не равны
б) равны по стороне и 2 прилежащим к ней углам;
в) равны по 3 сторонам;
г) Не равны
Слайд 49а) Равны по 2 сторонам и углу между ними;
б) равны по
стороне и 2 прилежащим к ней углам;
в) равны по 3 сторонам;
г) Не равны
в) равны по 3 сторонам;
г) Не равны
5. Треугольники изображенные на рисунке,
Тесты.
Слайд 546. Треугольники изображенные на рисунке,
Тесты.
а) Равны по 2 сторонам и углу
между ними;
б) равны по стороне и 2 прилежащим к ней углам;
в) равны по 3 сторонам;
г) Не равны
б) равны по стороне и 2 прилежащим к ней углам;
в) равны по 3 сторонам;
г) Не равны
Слайд 648. Гипотенузой треугольника АВС, изображенного на рисунке, является сторона:
Тесты.
а) АВ;
б) ВС;
в)
АС;
г) АВ и АС.
г) АВ и АС.
