- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Понятие многогранника
Содержание
- 1. Презентация по математике Понятие многогранника
- 2. Теория многогранников, в частности выпуклых многогранников, —
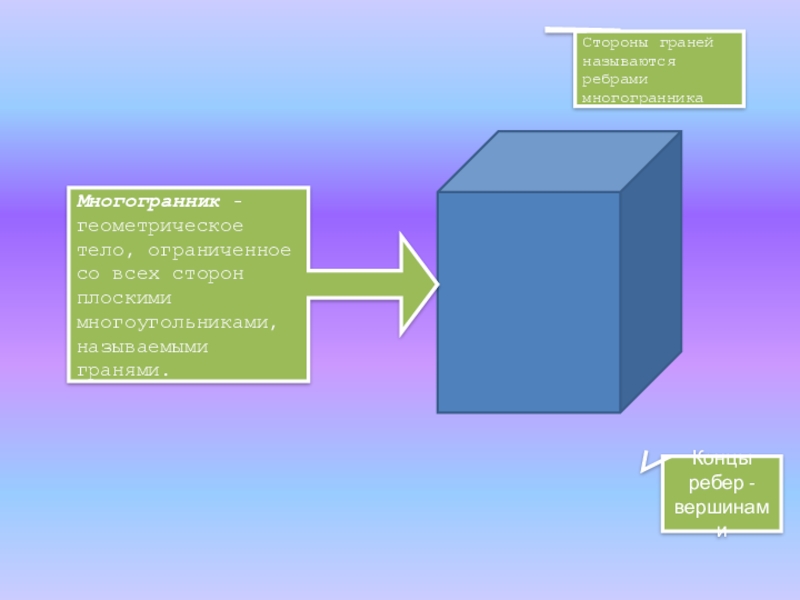
- 3. Стороны граней называются ребрами многогранникаМногогранник - геометрическое
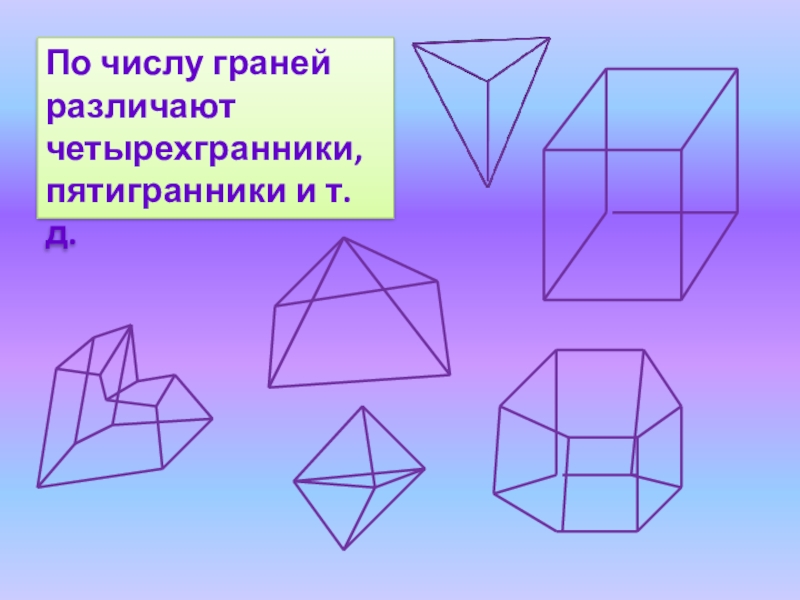
- 4. По числу граней различают четырехгранники, пятигранники и т. д.
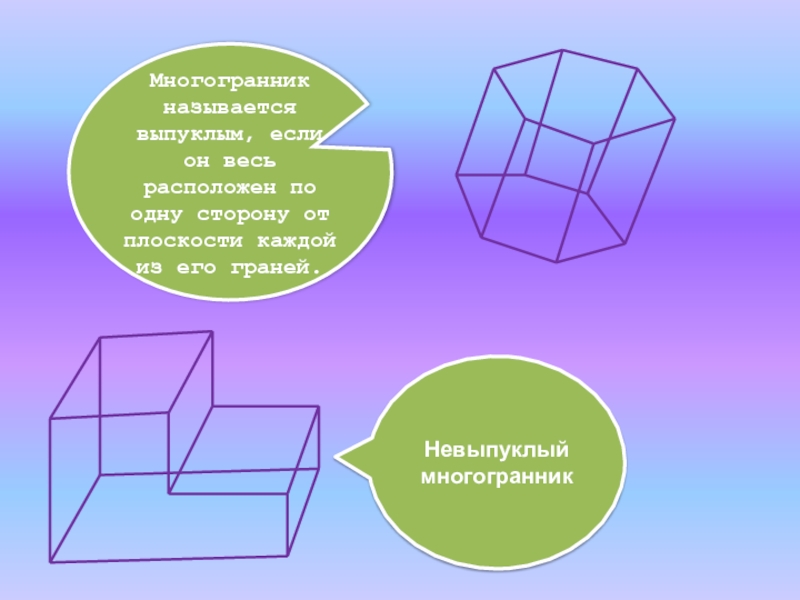
- 5. Невыпуклый многогранникМногогранник называется выпуклым, если он весь
- 6. Правильным называется многогранник,
- 7. В каждой
- 8. Правильный
- 9. Правильный
- 10. Правильный многогранник,
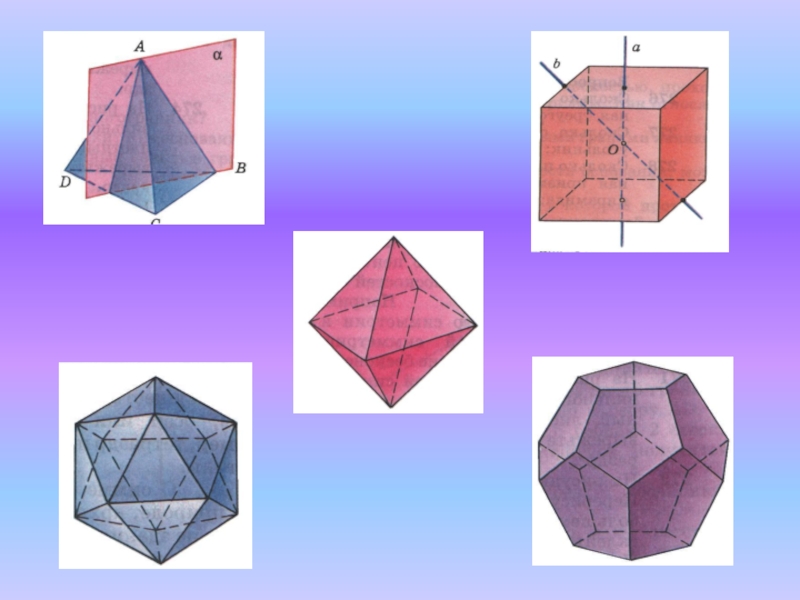
- 11. Додекаэдр Правильный многогранник, у которого грани правильные
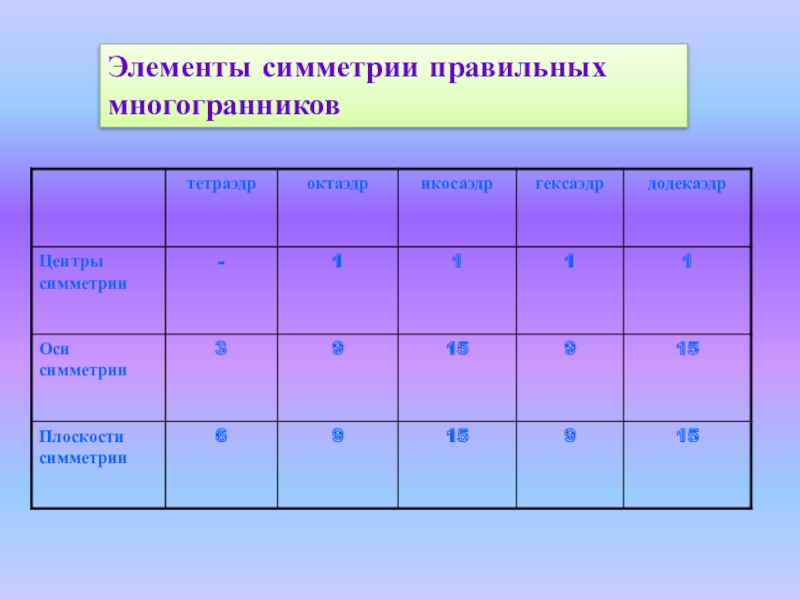
- 12. Элементы симметрии правильных многогранников
- 13. Слайд 13
- 14. Все типы
- 15. Правильные многогранники называют также «платоновыми телами» -
- 16. Олицетворение многогранников
- 17. Звездчатые правильные многогранники
- 18. . Существует семейство тел, родственных платоновым -
- 19. Если наблюдать и рассматривать многогранные формы, то
- 20. Замечено, что наша матушка-Земля последовательно проходит эволюцию
- 21. Если нанести на глобус очаги наиболее крупных
- 22. Слайд 22
- 23. Додекаэдрическая структура, по мнению Д. Винтера (американского
- 24. Впрочем, многогранники - отнюдь не только объект
- 25. Ярчайшим примером художественного изображения многогранников в XX
- 26. Доклад окончен. Спасибо, что не спали ☺
Слайд 1Понятие многогранника. Правильные многогранники.
Урок геометрии в 10 классе
Выполнила: Голенищева Зоя Тимофеевна,
МБОУ
Слайд 2Теория многогранников, в частности выпуклых многогранников, — одна из самых увлекательных глав
Слайд 3
Стороны граней называются ребрами многогранника
Многогранник - геометрическое тело, ограниченное со всех
Концы ребер - вершинами
Слайд 5
Невыпуклый многогранник
Многогранник называется выпуклым, если он весь расположен по одну сторону
Слайд 6
Правильным называется многогранник, у которого все грани
Приведён пример правильного многогранника (икосаэдр), его гранями являются правильные (равносторонние) треугольники.
Слайд 7 В каждой вершине многогранника должно сходиться
Слайд 8 Правильный многогранник, у которого грани
Тетраэдр
Слайд 9 Правильный многогранник, у которого грани-
Октаэдр
Слайд 10 Правильный многогранник, у которого грани –
Куб
Слайд 11Додекаэдр
Правильный многогранник, у которого грани правильные пятиугольники и в каждой
Слайд 14 Все типы правильных многогранников были известны
Немного истории
Слайд 15Правильные многогранники называют также «платоновыми телами» - они занимали видное место
Додекаэдр символизировал всё мироздание, почитался главнейшим. Уже по латыни в средние века его стали называть «пятая сущность» или guinta essentia, «квинта эссенциа», отсюда происходит вполне современное слово «квинтэссенция», означающее всё самое главное, основное, истинную сущность чего-либо.
Слайд 18.
Существует семейство тел, родственных платоновым - это полуправильные выпуклые многогранники,
Слайд 19Если наблюдать и рассматривать многогранные формы, то можно не только почувствовать
Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие — в виде вирусов, простейших микроорганизмов.
Кристаллы — тела, имеющие многогранную форму. Вот один из примеров таких тел: кристалл пирита (сернистый колчедан FeS) — природная модель додекаэдра. Пирит (от греч. “пир” — огонь) — сернистое железо или серный колчедан, наиболее распространенный минерал из группы сульфидов. Размеры кристаллов пирита часто достигают нескольких сантиметров и являются хорошим коллекционным материалом. От других подобных ему минералов отличается твердостью: царапает стекло.
Слайд 20Замечено, что наша матушка-Земля последовательно проходит эволюцию правильных объемных фигур. Существует
Существует гипотеза, по которой ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. «Лучи» этого кристалла, а точнее его силовое поле, обусловливают икосаэдро-додекаэдрическую структуру Земли, проявляющуюся в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. 62 их вершины и середины ребер, называемые узлами, оказывается, обладают рядом специфичecких свойств, позволяющих объяснить многие непонятные явления.
Слайд 21Если нанести на глобус очаги наиболее крупных и примечательных культур и
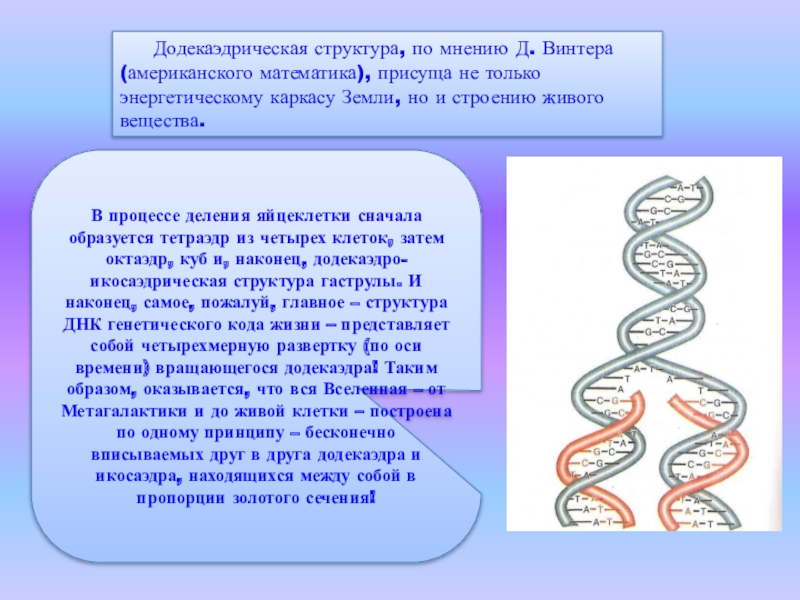
Слайд 23Додекаэдрическая структура, по мнению Д. Винтера (американского математика), присуща не только
В процессе деления яйцеклетки сначала образуется тетраэдр из четырех клеток, затем октаэдр, куб и, наконец, додекаэдро-икосаэдрическая структура гаструлы. И наконец, самое, пожалуй, главное – структура ДНК генетического кода жизни – представляет собой четырехмерную развертку (по оси времени) вращающегося додекаэдра! Таким образом, оказывается, что вся Вселенная – от Метагалактики и до живой клетки – построена по одному принципу – бесконечно вписываемых друг в друга додекаэдра и икосаэдра, находящихся между собой в пропорции золотого сечения!
Слайд 24Впрочем, многогранники - отнюдь не только объект научных исследований. Их формы
Слайд 25Ярчайшим примером художественного изображения многогранников в XX веке являются, конечно, графические
Мауриц Эшер в своих рисунках как бы открыл и интуитивно проиллюстрировал законы сочетания элементов симметрии, т.е. те законы, которые властвуют над кристаллами, определяя и их внешнюю форму, и их атомную структуру, и их физические свойства.
Математик, так же как и художник или поэт, создает узоры, и если
его узоры более устойчивы, то лишь потому, что они составлены из идей.